Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 33, 34, 35 sách giáo khoa Toán 11 tập 2.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Một vật bắt đầu chuyển động theo đường thẳng và quãng đường đi được sau t giây được tính bởi (s(t) = 2{t^2}), s(t) tính bằng mét.
Một vật bắt đầu chuyển động theo đường thẳng và quãng đường đi được sau t giây được tính bởi \(s(t) = 2{t^2}\), s(t) tính bằng mét.
a, Cho biết vận tốc trung bình ( đơn vị m/s) của vật trong khoảng thời gian [\({t_0};t\)] được tính bởi công thức \({v_{tb}} = \frac{{s(t) - s({t_0})}}{{t - {t_0}}}\). Hãy tính vận tốc trung bình trong các khoảng thời gian [\({t_0};t\)] với \({t_0} = 3\)và t lần lượt là 3,1 ; 3,01 ; 3,001. Sau đó hoàn thành Bảng 7.1
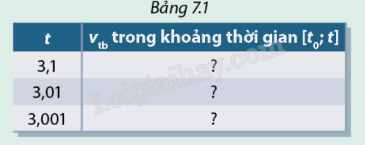
b, Vận tốc trung bình trong khoảng thời gian nào ở Bảng 7.1 gần nhất với vận tốc tại thời điểm \({t_0} = 3\)
c, Để vận tốc trung bình trong khoảng thời gian [\({t_0};t\)] càng gần với vận tốc tại thời điểm \({t_0}\)thì ta cần chọn giá trị của t như thế nào?
Phương pháp giải:
a, Áp dụng công thức \(s(t) = 2{t^2}\) và công thức \({v_{tb}} = \frac{{s(t) - s({t_0})}}{{t - {t_0}}}\) để tính vận tốc trung bình.
b, Dựa vào kết quả câu a để tìm giá trị vận tốc gần với vận tốc tại thời điểm \({t_0} = 3\)
c, Để vận tốc trung bình càng gần vận tốc tại thời điểm \({t_0}\)thì ta cần chọn giá trị của t càng gần thời điểm \({t_0}\).
Lời giải chi tiết:
a, Thay t = 3,1; t=3,01; t= 3,001 vào hàm số s(t) ta được:
\(s(3,1) = 2.3,{1^2} = 2.9,61 = 19,22\)\( \Rightarrow {v_{tb}} = \frac{{s(3,1) - s(3)}}{{3,1 - 3}} = \frac{{19,22 - 18}}{{0,1}} = 12,2\)
\(s(3,01) = 2.3,{01^2} = 2.9,0601 = 18,1202\)\( \Rightarrow {v_{tb}} = \frac{{s(3,01) - s(3)}}{{3,01 - 3}} = \frac{{18,1202 - 18}}{{0,01}} = 12,02\)
\(s(3,001) = 2.3,{001^2} = 2.9,006001 = 18,012002\)\( \Rightarrow {v_{tb}} = \frac{{s(3,001) - s(3)}}{{3,001 - 3}} = \frac{{18,012002 - 18}}{{0,001}} = 12,002\)

b, Từ kết quả câu a cho thấy vận tốc tại thời điểm t = 3,001 gần nhất với vận tốc tại thời điểm \({t_0} = 3\)
c, Từ kết quả câu b ta thấy để vận tốc trung bình càng gần vận tốc tại thời điểm \({t_0}\)thì ta cần chọn giá trị của t càng gần thời điểm \({t_0}\).
Tính đạo hàm của hàm số \(f(x) = \frac{2}{{x + 1}}\) tại điểm \({x_0} = 1\)
Phương pháp giải:
Sử dụng định nghĩa đạo hàm của hàm số tại một điểm
Lời giải chi tiết:
Ta có: \(\mathop {\lim }\limits_{x \to 1} \frac{{f(x) - f(1)}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{\frac{2}{{x + 1}} - 1}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{1 - x}}{{(x + 1).(x - 1)}}\mathop { = \lim }\limits_{x \to 1} \frac{{ - 1}}{{x + 1}} = \frac{{ - 1}}{2}\)
Xét tình huống vận động viên nhảy dù trong bài toán khởi động:
a, Tìm vận tốc của vận động viên nhảy dù sau 2 giây kể từ khi bắt đầu rơi tự do
b, Sau khi rơi tự do được 490 m, vận động viên đó bung dù để chuẩn bị đáp xuống mặt đất. Tìm vận tốc của vận động viên tại thời điểm bung dù.
Phương pháp giải:
a, Vận tốc của vận động viên sau 2 giây kể từ khi rơi tự do là đạo hàm của hàm số tại \({t_0} = 2\).
b, Tìm thời điểm mà vận động viên đi được 490 m, sau đó tính đạo hàm của hàm số tại thời điểm đó để xác định vận tốc tức thời.
Lời giải chi tiết:
a, Vận tốc của vận động viên sau 2 giây kể từ khi rơi tự do là:
\(\mathop {\lim }\limits_{t \to 2} \frac{{f(t) - f(2)}}{{t - 2}} = \mathop {\lim }\limits_{t \to 2} \frac{{4,9{t^2} - 19,6}}{{t - 2}} = \mathop {\lim }\limits_{t \to 2} \frac{{4,9.({t^2} - 4)}}{{t - 2}} = \mathop {\lim }\limits_{t \to 2} \frac{{4,9.(t - 2).(t + 2)}}{{t - 2}} = \mathop {\lim }\limits_{t \to 2} 4,9.(t + 2) = 19,6\)
Vậy vận tốc của vận động viên sau 2 giây kể từ khi rơi tự do là 19,6 m / s
b, Ta có: \(s({t_1}) = 4,9{t_1}^2 \Leftrightarrow 490 = 4,9.{t_1}^2 \Leftrightarrow {t_1}^2 = 100 \Rightarrow {t_1} = 10\)
Vận tốc của vận động viên tại thời điểm bung dù là:
\(\mathop {\lim }\limits_{t \to 10} \frac{{f(t) - f(10)}}{{t - 10}} = \mathop {\lim }\limits_{t \to 2} \frac{{4,9{t^2} - 490}}{{t - 10}} = \mathop {\lim }\limits_{t \to 2} \frac{{4,9.({t^2} - 100)}}{{t - 10}} = \mathop {\lim }\limits_{t \to 2} \frac{{4,9.(t - 10).(t + 10)}}{{t - 10}} = \mathop {\lim }\limits_{t \to 10} 4,9.(t + 10) = 98\)
Vậy vận tốc của vận động viên tại thời điểm bung dù là 98 m/s
Mục 1 của SGK Toán 11 tập 2 thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết các bài tập trong mục này một cách hiệu quả, học sinh cần nắm vững lý thuyết, công thức và phương pháp giải liên quan. Bài viết này sẽ đi sâu vào từng bài tập, cung cấp lời giải chi tiết và phân tích các bước thực hiện.
Trang 33 thường chứa các bài tập vận dụng kiến thức cơ bản của mục học. Chúng ta sẽ bắt đầu với việc xác định yêu cầu của bài toán, sau đó áp dụng các công thức và phương pháp phù hợp để tìm ra đáp án chính xác. Ví dụ, nếu bài toán yêu cầu tính giới hạn của một hàm số, chúng ta cần sử dụng các quy tắc tính giới hạn và các định lý liên quan.
Trang 34 thường chứa các bài tập nâng cao hơn, đòi hỏi học sinh phải có khả năng tư duy logic và vận dụng kiến thức một cách linh hoạt. Chúng ta sẽ phân tích kỹ từng bài toán, tìm ra các mối liên hệ giữa các yếu tố và xây dựng lời giải hợp lý. Ví dụ, nếu bài toán yêu cầu chứng minh một đẳng thức lượng giác, chúng ta cần sử dụng các công thức lượng giác và các phép biến đổi đại số để chứng minh đẳng thức đó.
Trang 35 thường chứa các bài tập tổng hợp, kết hợp nhiều kiến thức và kỹ năng khác nhau. Chúng ta sẽ tiếp cận các bài toán này một cách toàn diện, sử dụng các phương pháp giải phù hợp và kiểm tra lại kết quả để đảm bảo tính chính xác. Ví dụ, nếu bài toán yêu cầu giải một hệ phương trình, chúng ta cần sử dụng các phương pháp giải hệ phương trình như phương pháp thế, phương pháp cộng đại số hoặc phương pháp ma trận.
Kiến thức trong mục 1 của SGK Toán 11 tập 2 có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau, như vật lý, kỹ thuật, kinh tế và khoa học máy tính. Ví dụ, kiến thức về giới hạn được sử dụng để tính toán các đại lượng vật lý như vận tốc, gia tốc và lực. Kiến thức về đạo hàm được sử dụng để tối ưu hóa các hàm số và tìm ra các điểm cực trị. Kiến thức về tích phân được sử dụng để tính diện tích, thể tích và các đại lượng khác.
Để học tốt môn Toán 11, các em cần dành thời gian ôn tập lý thuyết, làm bài tập thường xuyên và tìm kiếm sự giúp đỡ khi gặp khó khăn. Hãy sử dụng giaitoan.edu.vn như một công cụ hỗ trợ đắc lực trong quá trình học tập của mình. Chúc các em học tốt!
| Công thức | Mô tả |
|---|---|
| lim (f(x) + g(x)) = lim f(x) + lim g(x) | Giới hạn của tổng |
| lim (f(x) * g(x)) = lim f(x) * lim g(x) | Giới hạn của tích |