Bài 8.44 trang 90 SGK Toán 11 tập 2

Bài 8.44 trang 90 SGK Toán 11 tập 2 - Cùng khám phá

Bài 8.44 trang 90 SGK Toán 11 tập 2 thuộc chương trình học Toán 11, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh nắm vững các quy tắc tính đạo hàm và kỹ năng giải phương trình, bất phương trình.

Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh hiểu rõ bản chất của bài toán và rèn luyện kỹ năng giải toán hiệu quả.

Cho tứ diện ABCD có hai mặt ABC và DBC là hai tam giác cân chung đáy BC. Trong các mệnh đề sau, mệnh đề nào đúng?

Đề bài

Cho tứ diện ABCD có hai mặt ABC và DBC là hai tam giác cân chung đáy BC. Trong các mệnh đề sau, mệnh đề nào đúng?

A. AB \( \bot \) CD.

B. AC \( \bot \) BD.

C. AD \( \bot \) BC.

D. AB \( \bot \) AD.

Phương pháp giải - Xem chi tiết Bài 8.44 trang 90 SGK Toán 11 tập 2 - Cùng khám phá 1

Để chứng minh a vuông góc b ta đi chứng minh a vuông góc với (P) chứa b.

Lời giải chi tiết

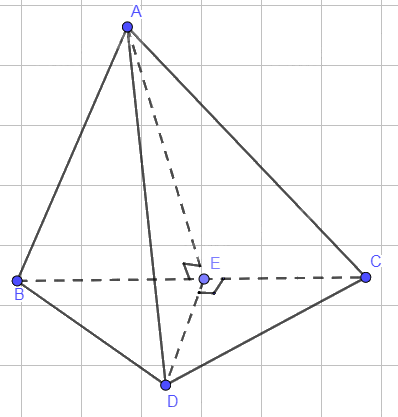
Bài 8.44 trang 90 SGK Toán 11 tập 2 - Cùng khám phá 2

Tam giác ABC cân tại A nên AE là đường cao đồng thời là đường trung tuyến \( \Rightarrow \) E là trung điểm BD \( \Rightarrow \)CE là đường trung tuyến của tam giác BCD.

Mà tam giác BDC cân tại D nên CE là đường cao hay \(CE \bot BD\).

Ta có:

\(\left\{ \begin{array}{l}AE \bot BC\\DE \bot BC\\AE \cap DE = E\\AE,DE \subset (ADE)\end{array} \right. \Rightarrow BC \bot (ADE)\)

Do đó,

\(\left\{ \begin{array}{l}BC \bot (ACE)\\AD \subset (ADE)\end{array} \right. \Rightarrow BC \bot AD\)

Chọn đáp án C.

Chinh phục Toán 11, mở rộng cánh cửa Đại học trong tầm tay! Khám phá ngay Bài 8.44 trang 90 SGK Toán 11 tập 2 - Cùng khám phá – hành trang không thể thiếu trong chuyên mục Sách giáo khoa Toán 11 trên nền tảng đề thi toán. Bộ bài tập toán trung học phổ thông được biên soạn chuyên sâu, bám sát chặt chẽ chương trình Toán lớp 11 và định hướng các kỳ thi quan trọng, cam kết tối ưu hóa toàn diện quá trình ôn luyện. Qua đó, học sinh không chỉ làm chủ kiến thức phức tạp mà còn rèn luyện tư duy giải quyết vấn đề, sẵn sàng cho các kỳ thi và chương trình đại học, nhờ phương pháp tiếp cận trực quan, logic và hiệu quả học tập vượt trội!

Bài 8.44 trang 90 SGK Toán 11 tập 2 - Giải chi tiết

Bài 8.44 trang 90 SGK Toán 11 tập 2 là một bài toán quan trọng trong chương trình học Toán 11, tập trung vào ứng dụng của đạo hàm trong việc tìm cực trị của hàm số. Để giải bài toán này, học sinh cần nắm vững các kiến thức sau:

Kiến thức về đạo hàm: Định nghĩa đạo hàm, quy tắc tính đạo hàm của các hàm số cơ bản (hàm đa thức, hàm lượng giác, hàm mũ, hàm logarit).
Điều kiện cần và đủ để hàm số đạt cực trị: Hàm số y = f(x) đạt cực đại tại x₀ nếu f'(x₀) = 0 và f''(x₀) < 0. Hàm số y = f(x) đạt cực tiểu tại x₀ nếu f'(x₀) = 0 và f''(x₀) > 0.
Phương pháp giải bài toán tìm cực trị: Bước 1: Tính đạo hàm bậc nhất f'(x). Bước 2: Tìm các điểm làm đạo hàm bậc nhất bằng 0 (nghiệm của phương trình f'(x) = 0). Bước 3: Tính đạo hàm bậc hai f''(x). Bước 4: Xét dấu đạo hàm bậc hai tại các điểm tìm được ở bước 2 để xác định cực đại, cực tiểu.

Giải bài toán Bài 8.44 trang 90 SGK Toán 11 tập 2

Để giải bài toán Bài 8.44 trang 90 SGK Toán 11 tập 2, chúng ta sẽ thực hiện các bước sau:

Xác định hàm số: Đầu tiên, chúng ta cần xác định hàm số cần tìm cực trị.
Tính đạo hàm bậc nhất: Tiếp theo, chúng ta tính đạo hàm bậc nhất của hàm số.
Tìm điểm dừng: Giải phương trình đạo hàm bậc nhất bằng 0 để tìm các điểm dừng của hàm số.
Tính đạo hàm bậc hai: Tính đạo hàm bậc hai của hàm số.
Xác định cực trị: Sử dụng đạo hàm bậc hai để xác định loại cực trị tại mỗi điểm dừng.
Kết luận: Kết luận về các điểm cực đại, cực tiểu của hàm số.

Ví dụ, xét hàm số y = x³ - 3x² + 2. Ta thực hiện các bước sau:

Đạo hàm bậc nhất: y' = 3x² - 6x
Điểm dừng: 3x² - 6x = 0 => x = 0 hoặc x = 2
Đạo hàm bậc hai: y'' = 6x - 6
Xác định cực trị: Tại x = 0, y'' = -6 < 0 => Hàm số đạt cực đại tại x = 0. Tại x = 2, y'' = 6 > 0 => Hàm số đạt cực tiểu tại x = 2.
Kết luận: Hàm số đạt cực đại tại x = 0, giá trị cực đại là y = 2. Hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là y = -2.

Lưu ý:

Khi giải bài toán tìm cực trị, cần kiểm tra xem các điểm dừng có thuộc tập xác định của hàm số hay không.
Nếu đạo hàm bậc hai tại một điểm dừng bằng 0, cần sử dụng các phương pháp khác để xác định loại cực trị (ví dụ: xét dấu đạo hàm bậc ba).

Bài 8.44 trang 90 SGK Toán 11 tập 2 là một bài toán điển hình để rèn luyện kỹ năng giải bài toán tìm cực trị của hàm số. Việc nắm vững các kiến thức và phương pháp giải bài toán này sẽ giúp học sinh tự tin hơn khi giải các bài toán tương tự trong các kỳ thi.

Các bài tập tương tự:

Bài 8.45 trang 90 SGK Toán 11 tập 2
Bài 8.46 trang 91 SGK Toán 11 tập 2

Hy vọng với lời giải chi tiết và hướng dẫn cụ thể này, các em học sinh sẽ hiểu rõ hơn về Bài 8.44 trang 90 SGK Toán 11 tập 2 và có thể tự tin giải các bài tập tương tự. Chúc các em học tập tốt!