Bài tập 10.13 trang 107 SGK Toán 9 tập 2 thuộc chương trình Toán 9 Kết nối tri thức, yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế. Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu, giúp các em học sinh hiểu rõ phương pháp và tự tin làm bài.
Chúng tôi luôn cố gắng cung cấp những lời giải chính xác, đầy đủ và dễ tiếp cận nhất, hỗ trợ tối đa cho quá trình học tập của các em.
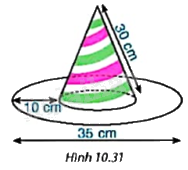
Chiếc mũ của chú hề với các kích thước như Hình 10.31. Hãy tính tổng diện tích vải cần để làm chiếc mũ (coi mép khâu không đáng kể và làm tròn kết quả đến hàng phần chục của (c{m^2})).
Đề bài
Chiếc mũ của chú hề với các kích thước như Hình 10.31. Hãy tính tổng diện tích vải cần để làm chiếc mũ (coi mép khâu không đáng kể và làm tròn kết quả đến hàng phần chục của \(c{m^2}\)).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+ Bán kính đường tròn đáy của hình nón là: \(r = \frac{{35 - 2.10}}{2} = 7,5\left( {cm} \right)\).
+ Tính diện tích xung quanh hình nón có bán kính \(\frac{{35}}{2}cm\) và đường sinh 30cm
+ Diện tích vành nón bằng hiệu diện tích hình tròn bán kính \(\frac{{35}}{2}cm\) và diện tích hình tròn bán kính \(\)\(\left( {\frac{{35}}{2} - 10} \right)cm = \frac{{15}}{2}cm\)
+ Diện tích vải cần dùng bằng tổng diện tích xung quanh của hình nón và diện tích vành nón.
Lời giải chi tiết
Bán kính đường tròn đáy của hình nón là:
\(r = \frac{{35 - 2.10}}{2} = 7,5\left( {cm} \right)\).
Diện tích xung quanh hình nón là:
\({S_{xq}} = \pi rl = \pi .7,5.30 = 225\pi \left( {c{m^2}} \right)\).
Diện tích vành nón là:
\({S_1} = \pi .17,{5^2} - \pi .7,{5^2} = 250\pi \left( {c{m^2}} \right)\).
Diện tích vải cần dùng là:
\(S = {S_{xq}} + {S_1} = 225\pi + 250\pi = 475\pi \approx 1492,3\left( {c{m^2}} \right)\).
Bài tập 10.13 SGK Toán 9 tập 2 Kết nối tri thức là một bài toán ứng dụng thực tế về hàm số bậc hai. Để giải bài tập này, học sinh cần nắm vững các kiến thức về:
Nội dung bài tập:
Một quả bóng được ném lên từ mặt đất với vận tốc ban đầu là 15 m/s. Giả sử rằng quả bóng chuyển động theo phương thẳng đứng và chỉ chịu tác dụng của trọng lực. Hãy viết hàm số biểu diễn độ cao h (mét) của quả bóng theo thời gian t (giây).
Lời giải:
Ta có thể sử dụng công thức tính độ cao của vật ném lên theo phương thẳng đứng:
h(t) = v0t - (1/2)gt2
Trong đó:
Thay v0 = 15 m/s và g = 9.8 m/s2 vào công thức, ta được:
h(t) = 15t - (1/2)(9.8)t2
h(t) = 15t - 4.9t2
Vậy hàm số biểu diễn độ cao h (mét) của quả bóng theo thời gian t (giây) là h(t) = 15t - 4.9t2.
Hàm số h(t) = 15t - 4.9t2 là một hàm số bậc hai với a = -4.9, b = 15, c = 0.
Vì a < 0 nên hàm số có đồ thị là một parabol quay xuống.
Tọa độ đỉnh của parabol là:
x0 = -b / (2a) = -15 / (2 * -4.9) ≈ 1.53 s
y0 = h(x0) = h(1.53) = 15 * 1.53 - 4.9 * (1.53)2 ≈ 11.48 m
Vậy đỉnh của parabol là (1.53; 11.48). Điều này có nghĩa là quả bóng đạt độ cao tối đa khoảng 11.48 mét sau khoảng 1.53 giây.
Hàm số đồng biến trên khoảng (-∞; 1.53) và nghịch biến trên khoảng (1.53; +∞).
Để củng cố kiến thức về hàm số bậc hai và ứng dụng vào giải quyết các bài toán thực tế, các em có thể tự giải các bài tập tương tự sau:
Kết luận:
Bài tập 10.13 trang 107 SGK Toán 9 tập 2 Kết nối tri thức là một bài toán ứng dụng thực tế giúp học sinh hiểu rõ hơn về hàm số bậc hai và cách sử dụng hàm số để mô tả các hiện tượng trong đời sống. Việc nắm vững kiến thức về hàm số bậc hai là rất quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình Toán 9 và các chương trình học tiếp theo.