Chào mừng bạn đến với bài học lý thuyết về hàm số bậc hai y = ax² (a ≠ 0) trong chương trình Toán 9 Kết nối tri thức. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về hàm số này, giúp bạn tự tin giải quyết các bài tập liên quan.
Chúng ta sẽ cùng nhau tìm hiểu về định nghĩa, các yếu tố cơ bản của hàm số, cách xác định đồ thị và ứng dụng của hàm số y = ax² (a ≠ 0) trong thực tế.
1. Hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) Hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) xác định với mọi giá trị x thuộc \(\mathbb{R}\).
1. Hàm số \(y = a{x^2}\left( {a \ne 0} \right)\)
Hàm số \(y = a{x^2}\left( {a \ne 0} \right)\)xác định với mọi giá trị x thuộc \(\mathbb{R}\). |
Ví dụ: Hàm số \(y = 2{x^2},y = - \frac{3}{2}{x^2}\) là các hàm số có dạng \(y = a{x^2}\left( {a \ne 0} \right)\).
2. Đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\)
Cách vẽ đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\)
- Lập bảng ghi một số cặp giá trị tương ứng của x và y. - Trong mặt phẳng tọa độ Oxy, biểu diễn các cặp điểm (x; y) trong bảng giá trị trên và nối chúng lại để được một đường cong là đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\). |
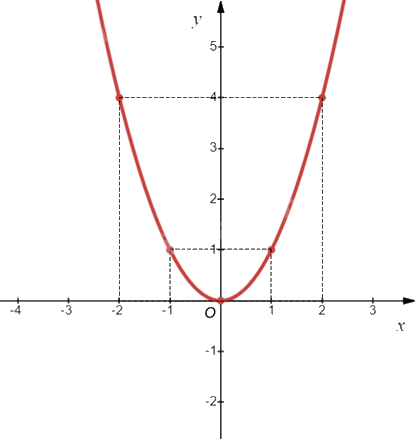
Ví dụ: Vẽ đồ thị của hàm số \(y = {x^2}\).
Lập bảng một số giá trị tương ứng giữa x và y:

Biểu diễn các điểm \(\left( { - 2;4} \right)\), \(\left( { - 1;1} \right)\), \(\left( {0;0} \right)\), \(\left( {1;1} \right)\), \(\left( {2;4} \right)\) trên mặt phẳng tọa độ Oxy và nối chúng lại với nhau, ta được đồ thị hàm số \(y = {x^2}\) như hình vẽ sau:
Tính đối xứng của đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\)
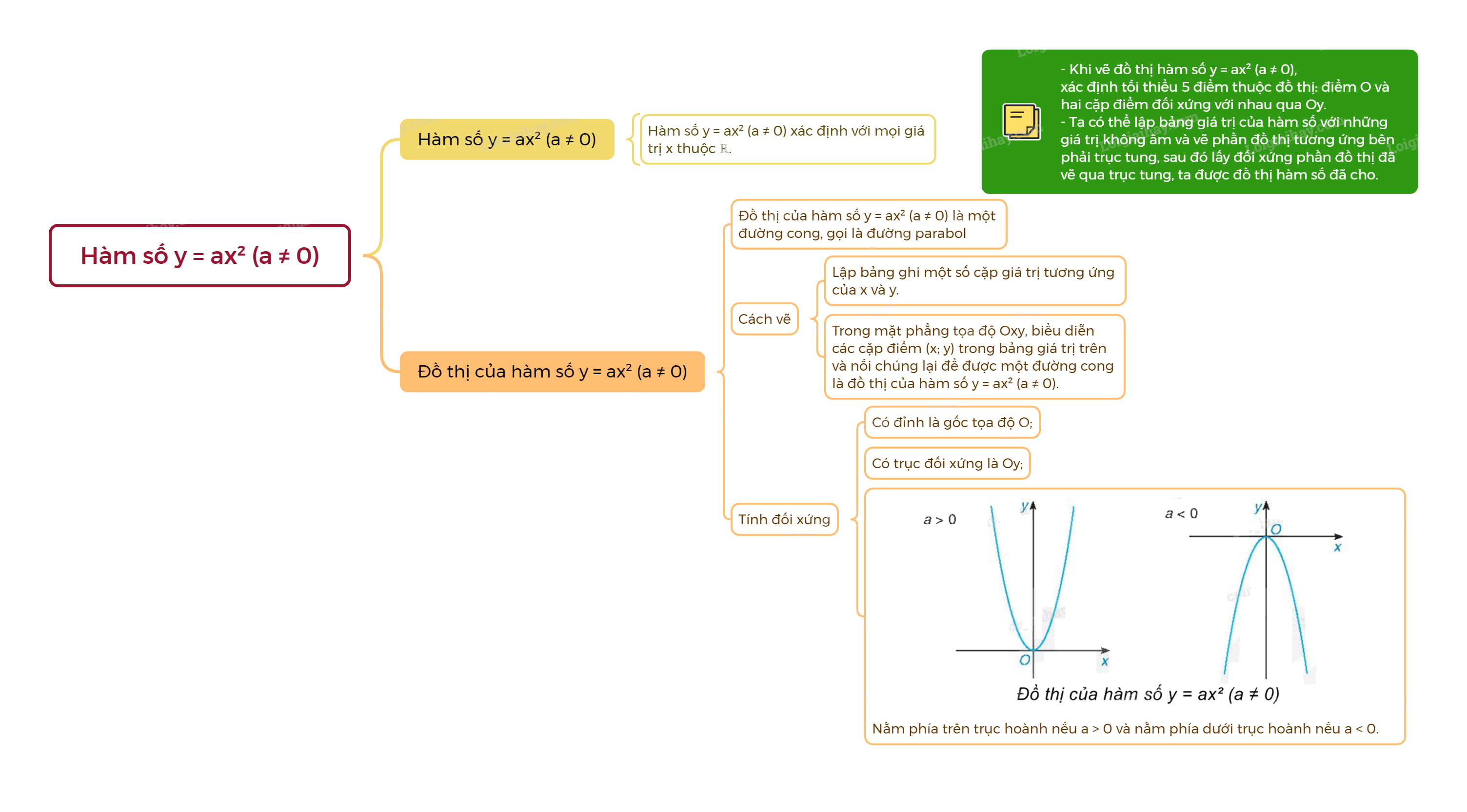
Đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) là một đường cong, gọi là đường parabol, có các tính chất sau: - Có đỉnh là gốc tọa độ O; - Có trục đối xứng là Oy; - Nằm phía trên trục hoành nếu a > 0 và nằm phía dưới trục hoành nếu a < 0.
|
Nhận xét:
- Khi vẽ đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\), ta cần xác định tối thiểu 5 điểm thuộc đồ thị là gốc tọa độ O và hai cặp điểm đối xứng với nhau qua trục tung Oy.
- Do đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) nhận trục tung Oy là trục đối xứng nên ta có thể lập bảng giá trị của hàm số này với những giá trị x không âm và vẽ phần đồ thị tương ứng ở bên phải trục tung, sau đó lấy đối xứng phần đồ thị đã vẽ qua trục tung ta sẽ được đồ thị của hàm số đã cho.
Hàm số bậc hai y = ax² (a ≠ 0) là một trong những hàm số quan trọng trong chương trình Toán 9. Việc nắm vững lý thuyết về hàm số này là nền tảng để giải quyết các bài toán liên quan đến đồ thị, ứng dụng và các bài toán thực tế.
Hàm số bậc hai có dạng y = ax² + bx + c, trong đó a, b, c là các số thực và a ≠ 0. Trong trường hợp này, chúng ta xét hàm số y = ax² (a ≠ 0), là một trường hợp đặc biệt của hàm số bậc hai với b = 0 và c = 0.
Tập xác định của hàm số y = ax² là tập hợp tất cả các số thực, ký hiệu là ℝ. Điều này có nghĩa là hàm số có thể nhận bất kỳ giá trị nào của x.
Tập giá trị của hàm số phụ thuộc vào giá trị của a:
Đồ thị của hàm số y = ax² là một parabol có đỉnh tại gốc tọa độ O(0; 0) và trục đối xứng là trục Oy.
Hình dạng của parabol phụ thuộc vào giá trị của a:
Đỉnh của parabol là điểm có tọa độ (0; 0).
Trục đối xứng của parabol là đường thẳng x = 0 (trục Oy).
Tiêu điểm của parabol là điểm F(0; 1/(4a)).
Đường chuẩn của parabol là đường thẳng y = -1/(4a).
Để kiểm tra một điểm M(x₀; y₀) có thuộc đồ thị của hàm số y = ax² hay không, ta thay x₀ vào hàm số và kiểm tra xem y₀ có bằng ax₀² hay không.
Hàm số y = ax² là hàm số chẵn, nghĩa là y(-x) = y(x) với mọi x thuộc tập xác định. Do đó, đồ thị của hàm số đối xứng qua trục Oy.
Sự biến thiên của hàm số phụ thuộc vào giá trị của a:
Hàm số y = ax² có nhiều ứng dụng trong thực tế, ví dụ như:
Để củng cố kiến thức về hàm số y = ax², bạn có thể thực hành giải các bài tập sau:
Hy vọng bài học này đã giúp bạn hiểu rõ hơn về lý thuyết hàm số y = ax² (a ≠ 0) Toán 9 Kết nối tri thức. Chúc bạn học tốt!