Giải bài tập 5.1 trang 86 SGK Toán 9 tập 1 - Kết nối tri thức

Bài tập 5.1 trang 86 SGK Toán 9 tập 1 thuộc chương Hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế. Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và làm bài tập hiệu quả.

Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 9 tập 1 - Kết nối tri thức.

Trong mặt phẳng tọa độ Oxy, cho các điểm M (0 ; 2), N (0; -3) và P(2; -1). Vẽ hình và cho biết trong các điểm đã cho, điểm nào nằm trên, điểm nào nằm trong, điểm nào nằm ngoài đường tròn (left( {O;sqrt 5 } right))? Vì sao?

Đề bài

Trong mặt phẳng tọa độ Oxy, cho các điểm M (0 ; 2), N (0; -3) và P(2; -1). Vẽ hình và cho biết trong các điểm đã cho, điểm nào nằm trên, điểm nào nằm trong, điểm nào nằm ngoài đường tròn \(\left( {O;\sqrt 5 } \right)\)? Vì sao?

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết Giải bài tập 5.1 trang 86 SGK Toán 9 tập 1 - Kết nối tri thức 1

Vẽ đường tròn \(\left( {O;\sqrt 5 } \right)\) và các điểm M (0; 2), N (0; -3) và P(2; -1). Sau đó dựa vào hình vẽ xác định điểm nào nằm trên, điểm nào nằm trong, điểm nào nằm ngoài đường tròn \(\left( {O;\sqrt 5 } \right)\).

Lời giải chi tiết

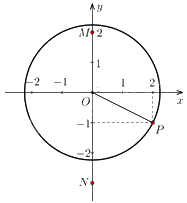
Giải bài tập 5.1 trang 86 SGK Toán 9 tập 1 - Kết nối tri thức 2

Vì \(OM = 2 < \sqrt 5 = R\) nên điểm M nằm trong đường tròn.

Vì OP là đường chéo của tam giác vuông có cạnh là 1 và 2 nên \(OP = \sqrt{1^2+2^2} = \sqrt 5 = R\) nên P nằm trên đường tròn.

Vì \(ON = 3 > \sqrt 5 = R\) nên điểm N nằm ngoài đường tròn.

Làm chủ Toán 9, tự tin vào phòng thi! Đừng bỏ lỡ Giải bài tập 5.1 trang 86 SGK Toán 9 tập 1 - Kết nối tri thức đặc sắc thuộc chuyên mục toán 9 sgk trên nền tảng toán math. Với bộ bài tập lý thuyết toán thcs được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình sách giáo khoa mới nhất, đây chính là công cụ đắc lực giúp các em tối ưu hóa ôn luyện, củng cố kiến thức vững chắc và thuần thục mọi dạng bài thi khó nhằn. Phương pháp học trực quan, khoa học sẽ mang lại hiệu quả vượt trội, giúp con bạn chinh phục mọi thử thách một cách dễ dàng.

Giải bài tập 5.1 trang 86 SGK Toán 9 tập 1 - Kết nối tri thức: Hướng dẫn chi tiết

Bài tập 5.1 trang 86 SGK Toán 9 tập 1 - Kết nối tri thức là một bài tập quan trọng trong chương Hàm số bậc nhất. Để giải bài tập này, học sinh cần nắm vững các khái niệm cơ bản về hàm số bậc nhất, bao gồm:

Định nghĩa hàm số bậc nhất: Hàm số bậc nhất có dạng y = ax + b, trong đó a và b là các số thực, a ≠ 0.
Hệ số a: Hệ số a xác định độ dốc của đường thẳng biểu diễn hàm số. Nếu a > 0, hàm số đồng biến; nếu a < 0, hàm số nghịch biến.
Hệ số b: Hệ số b là tung độ gốc, tức là giao điểm của đường thẳng với trục Oy.

Nội dung bài tập 5.1:

Cho hàm số y = 2x + 3. Hãy tìm:

Giá trị của y khi x = -2.
Giá trị của x khi y = 5.

Lời giải chi tiết

a) Tìm giá trị của y khi x = -2

Để tìm giá trị của y khi x = -2, ta thay x = -2 vào hàm số y = 2x + 3:

y = 2 * (-2) + 3 = -4 + 3 = -1

Vậy, khi x = -2 thì y = -1.

b) Tìm giá trị của x khi y = 5

Để tìm giá trị của x khi y = 5, ta thay y = 5 vào hàm số y = 2x + 3:

5 = 2x + 3

2x = 5 - 3

2x = 2

x = 2 / 2

x = 1

Vậy, khi y = 5 thì x = 1.

Lưu ý khi giải bài tập

Khi giải bài tập về hàm số bậc nhất, học sinh cần chú ý:

Đọc kỹ đề bài để xác định đúng các thông tin cần tìm.
Vận dụng đúng công thức và các khái niệm liên quan đến hàm số bậc nhất.
Kiểm tra lại kết quả để đảm bảo tính chính xác.

Bài tập tương tự

Để củng cố kiến thức về hàm số bậc nhất, học sinh có thể làm thêm các bài tập tương tự sau:

Bài tập 5.2 trang 86 SGK Toán 9 tập 1 - Kết nối tri thức
Bài tập 5.3 trang 87 SGK Toán 9 tập 1 - Kết nối tri thức

Kết luận

Bài tập 5.1 trang 86 SGK Toán 9 tập 1 - Kết nối tri thức là một bài tập cơ bản về hàm số bậc nhất. Hy vọng với lời giải chi tiết và hướng dẫn trên, các em học sinh sẽ hiểu rõ hơn về bài tập này và làm bài tập hiệu quả hơn. Chúc các em học tốt!

Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.