Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tập 1 của giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong SGK Toán 9 tập 1 - Kết nối tri thức, giúp các em nắm vững kiến thức và tự tin hơn trong học tập.
Ở bài viết này, chúng ta sẽ cùng nhau giải quyết các bài tập trong mục 1 trang 67, 68, 69. Các lời giải được trình bày một cách rõ ràng, logic, kèm theo các ví dụ minh họa để các em dễ dàng theo dõi và áp dụng.
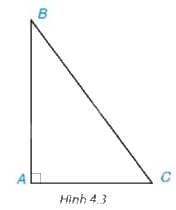
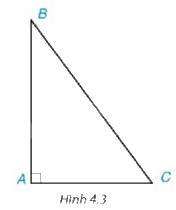
Xét góc C của tam giác ABC vuông tại A (H.4.3) . Hãy chỉ ra cạnh đối và cạnh kề của góc C.
Video hướng dẫn giải
Trả lời câu hỏi Câu hỏi trang 67 SGK Toán 9 Kết nối tri thức
Xét góc C của tam giác ABC vuông tại A (H.4.3) . Hãy chỉ ra cạnh đối và cạnh kề của góc C.
Phương pháp giải:
Góc B tạo bởi hai cạnh là AB và BC trong đó cạnh BC là cạnh huyền và cạnh AB là cạnh kề, cạnh còn lại của tam giác là cạnh đối.
Lời giải chi tiết:
Góc C có cạnh đối là AB và cạnh kề của góc C là AC.
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 2 trang 70 SGK Toán 9 Kết nối tri thức
Cho tam giác ABC vuông tại A có \(\widehat C = {45^0}\) và \(AB = c.\) Tính BC và AC theo c.
Phương pháp giải:
Từ công thức lượng giác liên quan đến góc C, ta tính được các cạnh còn lại theo AB.
Tỉ số giữa cạnh đối và cạnh huyền gọi là sin của góc C, kí hiệu \(\sin \widehat C\)
Tỉ số giữa cạnh đối và cạnh kề của góc C gọi là \(\tan \widehat C\)
Lời giải chi tiết:
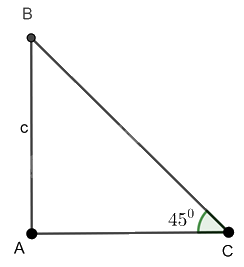
Ta có: \(\tan \widehat C = \frac{{AB}}{{AC}}\) suy ra \(\tan {45^0} = \frac{c}{{AC}}\) do đó \(1 = \frac{c}{{AC}}\) hay \(AC = c\)
\(\sin \widehat C = \frac{{AB}}{{BC}}\) suy ra \(\sin {45^0} = \frac{c}{{BC}}\) do đó \(\frac{{\sqrt 2 }}{2} = \frac{c}{{BC}}\) hay \(BC = \frac{{2c}}{{\sqrt 2 }} = \sqrt 2 c\)
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 69 SGK Toán 9 Kết nối tri thức
Cho tam giác ABC vuông cân tại A và \(AB = AC = a\) (H.4.7a).
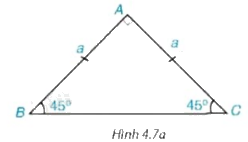
a) Hãy tính BC và các tỉ số \(\frac{{AB}}{{BC}}\) và \(\frac{{AC}}{{BC}}.\) Từ đó suy ra \(\sin {45^0};\cos {45^0}.\)
b) Hãy tính các tỉ số \(\frac{{AB}}{{AC}}\) và \(\frac{{AC}}{{AB}}.\) Từ đó suy ra \(\tan {45^0};\cot {45^0}.\)
Phương pháp giải:
Tính BC theo định lý Pythagore ta có: \(B{C^2} = A{B^2} + A{C^2}\)
Để tính các tỉ số ta thay các độ đo tương ứng của các cạnh.
Lời giải chi tiết:
Tam giác ABC vuông tại A, ta có: \(B{C^2} = A{B^2} + A{C^2}\) (Định lý Pythagore)
Nên \(B{C^2} = {a^2} + {a^2} = 2{a^2}\) suy ra \(BC = a\sqrt 2 \)
a) Tỉ số \(\frac{{AB}}{{BC}} = \frac{a}{{a\sqrt 2 }} = \frac{1}{{\sqrt 2 }} = \frac{{\sqrt 2 }}{2}\) và \(\frac{{AC}}{{BC}} = \frac{a}{{a\sqrt 2 }} = \frac{1}{{\sqrt 2 }} = \frac{{\sqrt 2 }}{2}\).
Do đó \(\sin {45^0} = \sin \widehat B = \frac{{AC}}{{BC}} = \frac{{\sqrt 2 }}{2};\) \(\cos {45^0} = \cos \widehat B = \frac{{AB}}{{BC}} = \frac{{\sqrt 2 }}{2}.\)
b) Tỉ số \(\frac{{AB}}{{AC}} = \frac{a}{a} = 1;\) \(\frac{{AC}}{{AB}} = \frac{a}{a} = 1\)
Do đó \(\tan {45^0} = \tan \widehat B = \frac{{AC}}{{AB}} = 1;\) \(\cot {45^0} = \cot \widehat B = \frac{{AB}}{{AC}} = 1\)
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 1 trang 67 SGK Toán 9 Kết nối tri thức
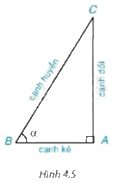
Cho tam giác ABC vuông tại A và tam giác A’B’C’ vuông tại A’ có \(\widehat B = \widehat {B'} = \alpha .\) Chứng minh rằng:
a) \(\Delta ABC\backsim \Delta A'B'C';\)
b) \(\frac{{AC}}{{BC}} = \frac{{A'C'}}{{B'C'}};\frac{{AB}}{{BC}} = \frac{{A'B'}}{{B'C'}};\frac{{AC}}{{AB}} = \frac{{A'C'}}{{A'B'}};\frac{{AB}}{{AC}} = \frac{{A'B'}}{{A'C'}}\)
Phương pháp giải:
Chứng minh tam giác đồng dạng theo trường hợp góc – góc (tam giác có hai cặp góc tương ứng bằng nhau) , sử dụng tính chất của tỉ lệ thức để chứng minh ý b (\(\frac{a}{b} = \frac{c}{d}\) suy ra \(\frac{a}{c} = \frac{b}{d}\) và \(\frac{b}{a} = \frac{d}{c}\) (tính chất tỉ lệ thức) ) .
Lời giải chi tiết:
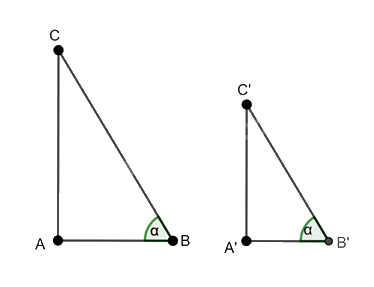
a) Xét hai tam giác ABC và tam giác A’B’C’ ta có:
\(\begin{array}{l}\widehat A = \widehat {A'} = {90^0}\\\widehat B = \widehat {B'} = \alpha \end{array}\)
Nên \(\Delta ABC\backsim \Delta A'B'C'\left( g-g \right)\)
b) \(\Delta ABC\backsim \Delta A'B'C'\) suy ra \(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{AC}}{{A'C'}}\) (tỉ lệ các cạnh tương ứng)
Do \(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}}\) nên ta có \(\frac{{AB}}{{BC}} = \frac{{A'B'}}{{B'C'}}\) (tính chất tỉ lệ thức)
Do \(\frac{{BC}}{{B'C'}} = \frac{{AC}}{{A'C'}}\) nên ta có \(\frac{{A'C'}}{{B'C'}} = \frac{{AC}}{{BC}}\) (tính chất tỉ lệ thức)
Do \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}}\) nên ta có \(\frac{{AB}}{{AC}} = \frac{{A'B'}}{{A'C'}}\) và \(\frac{{AC}}{{AB}} = \frac{{A'B'}}{{A'C'}}\) (tính chất tỉ lệ thức)
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 3 trang 69 SGK Toán 9 Kết nối tri thức
Xét tam giác đều ABC có cạnh bằng 2a.
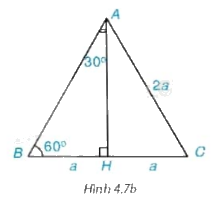
a) Tính đường cao AH của tam giác ABC (H.4.7b) .
b) Tính \(\sin {30^0};\cos {30^0};\sin {60^0};\cos {60^0}.\)
c) Tính \(\tan {30^0};\cot {30^0};\tan {60^0};\cot {60^0}.\)
Phương pháp giải:
Chú ý trong tam giác đều, đường cao vừa là đường phân giác vừa là đường trung tuyến. Từ đó ta tính được cạnh AH và các tỉ số lượng giác liên quan.
Lời giải chi tiết:
a) Tam giác ABC đều có đường cao AH nên AH cũng là đường trung tuyến của tam giác. Do đó ta có H là trung điểm của BC nên \(BH = HC = \frac{{BC}}{2} = \frac{{2a}}{2} = a\)
Xét tam giác ABH vuông tại H, ta có: \(A{B^2} = A{H^2} + H{B^2}\) (Đjnh lý Pythagore)
Suy ra \({\left( {2a} \right)^2} = A{H^2} + {a^2}\) nên \(A{H^2} = 3a\) hay \(AH = a\sqrt 3 \)
b) Tam giác ABC đều nên \(\widehat A = \widehat B = \widehat C = {60^0}\)
Nên \(\cos {60^0} = \cos \widehat B = \frac{{BH}}{{AB}} = \frac{a}{{2a}} = \frac{1}{2};\) \(\sin {60^0} = \sin \widehat B = \frac{{AH}}{{AB}} = \frac{{a\sqrt 3 }}{{2a}} = \frac{{\sqrt 3 }}{2}\)
Tam giác ABC đều nên AH vừa là đường cao vừa là đường phân giác của góc A, do đó \(\widehat {BAH} = \widehat {CAH} = \frac{{\widehat {BAC}}}{2} = \frac{{{{60}^0}}}{2} = {30^0}\)
\(\sin {30^0} = \sin \widehat {BAH} = \frac{{BH}}{{AB}} = \frac{a}{{2a}} = \frac{1}{2};\) \(\cos {30^0} = \cos \widehat {BAH} = \frac{{AH}}{{AB}} = \frac{{a\sqrt 3 }}{{2a}} = \frac{{\sqrt 3 }}{2}\)
c) \(\tan {30^0} = \tan \widehat {BAH} = \frac{{BH}}{{AH}} = \frac{a}{{a\sqrt 3 }} = \frac{{\sqrt 3 }}{3}\)
\(\cot {30^0} = \cot \widehat {BAH} = \frac{{AH}}{{BH}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3 \)
\(\tan {60^0} = \tan \widehat {ABH} = \frac{{AH}}{{BH}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3 \)
\(\cot {60^0} = \tan \widehat {ABH} = \frac{{BH}}{{AH}} = \frac{a}{{a\sqrt 3 }} = \frac{{\sqrt 3 }}{3}\)
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 1 trang 68SGK Toán 9 Kết nối tri thức
Cho tam giác ABC vuông tại A có AB = 5 cm, AC = 12 cm. Hãy tính các tỉ số lượng giác của góc B.
Phương pháp giải:
Xét tam giác ABC vuông tại A, ta có:
Tỉ số giữa cạnh đối và cạnh huyền gọi là sin của góc B, kí hiệu \(\sin \widehat B\)
Tỉ số giữa cạnh kề và cạnh huyền gọi là cosin của góc B, kí hiệu \(\cos \widehat B\)
Tỉ số giữa cạnh đối và cạnh kề của góc B gọi là \(\tan \widehat B\)
Tỉ số giữa cạnh kề và cạnh đối của góc B gọi là \(\cot \widehat B\)
Ở bài toán này ta còn thiếu cạnh huyền BC, do đó cần sử dụng định Pythagore để tính.
Lời giải chi tiết:
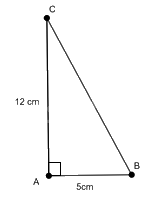
Xét tam giác ABC vuông tại A, ta có \(B{C^2} = A{B^2} + A{C^2}\) (Định lý Pythagore)
Nên \(B{C^2} = {5^2} + {12^2} = 169\) suy ra \(BC = 13\) (cm) .
Theo định nghĩa của tỉ số lượng giác ta có:
\(\sin \widehat B = \frac{{AC}}{{BC}} = \frac{{12}}{{13}};\\\cos \widehat B = \frac{{AB}}{{BC}} = \frac{5}{{13}};\\\tan \widehat B = \frac{{AC}}{{AB}} = \frac{{12}}{5};\\\cot \widehat B = \frac{{AB}}{{AC}} = \frac{5}{{12}}\)
Video hướng dẫn giải
Trả lời câu hỏi Câu hỏi trang 67 SGK Toán 9 Kết nối tri thức
Xét góc C của tam giác ABC vuông tại A (H.4.3) . Hãy chỉ ra cạnh đối và cạnh kề của góc C.
Phương pháp giải:
Góc B tạo bởi hai cạnh là AB và BC trong đó cạnh BC là cạnh huyền và cạnh AB là cạnh kề, cạnh còn lại của tam giác là cạnh đối.
Lời giải chi tiết:
Góc C có cạnh đối là AB và cạnh kề của góc C là AC.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 1 trang 67 SGK Toán 9 Kết nối tri thức
Cho tam giác ABC vuông tại A và tam giác A’B’C’ vuông tại A’ có \(\widehat B = \widehat {B'} = \alpha .\) Chứng minh rằng:
a) \(\Delta ABC\backsim \Delta A'B'C';\)
b) \(\frac{{AC}}{{BC}} = \frac{{A'C'}}{{B'C'}};\frac{{AB}}{{BC}} = \frac{{A'B'}}{{B'C'}};\frac{{AC}}{{AB}} = \frac{{A'C'}}{{A'B'}};\frac{{AB}}{{AC}} = \frac{{A'B'}}{{A'C'}}\)
Phương pháp giải:
Chứng minh tam giác đồng dạng theo trường hợp góc – góc (tam giác có hai cặp góc tương ứng bằng nhau) , sử dụng tính chất của tỉ lệ thức để chứng minh ý b (\(\frac{a}{b} = \frac{c}{d}\) suy ra \(\frac{a}{c} = \frac{b}{d}\) và \(\frac{b}{a} = \frac{d}{c}\) (tính chất tỉ lệ thức) ) .
Lời giải chi tiết:
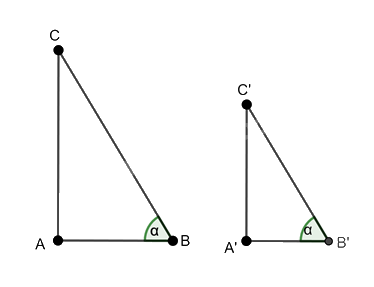
a) Xét hai tam giác ABC và tam giác A’B’C’ ta có:
\(\begin{array}{l}\widehat A = \widehat {A'} = {90^0}\\\widehat B = \widehat {B'} = \alpha \end{array}\)
Nên \(\Delta ABC\backsim \Delta A'B'C'\left( g-g \right)\)
b) \(\Delta ABC\backsim \Delta A'B'C'\) suy ra \(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{AC}}{{A'C'}}\) (tỉ lệ các cạnh tương ứng)
Do \(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}}\) nên ta có \(\frac{{AB}}{{BC}} = \frac{{A'B'}}{{B'C'}}\) (tính chất tỉ lệ thức)
Do \(\frac{{BC}}{{B'C'}} = \frac{{AC}}{{A'C'}}\) nên ta có \(\frac{{A'C'}}{{B'C'}} = \frac{{AC}}{{BC}}\) (tính chất tỉ lệ thức)
Do \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}}\) nên ta có \(\frac{{AB}}{{AC}} = \frac{{A'B'}}{{A'C'}}\) và \(\frac{{AC}}{{AB}} = \frac{{A'B'}}{{A'C'}}\) (tính chất tỉ lệ thức)
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 1 trang 68SGK Toán 9 Kết nối tri thức
Cho tam giác ABC vuông tại A có AB = 5 cm, AC = 12 cm. Hãy tính các tỉ số lượng giác của góc B.
Phương pháp giải:
Xét tam giác ABC vuông tại A, ta có:
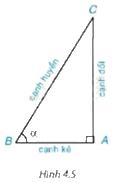
Tỉ số giữa cạnh đối và cạnh huyền gọi là sin của góc B, kí hiệu \(\sin \widehat B\)
Tỉ số giữa cạnh kề và cạnh huyền gọi là cosin của góc B, kí hiệu \(\cos \widehat B\)
Tỉ số giữa cạnh đối và cạnh kề của góc B gọi là \(\tan \widehat B\)
Tỉ số giữa cạnh kề và cạnh đối của góc B gọi là \(\cot \widehat B\)
Ở bài toán này ta còn thiếu cạnh huyền BC, do đó cần sử dụng định Pythagore để tính.
Lời giải chi tiết:
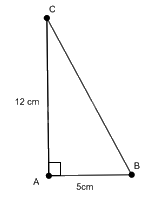
Xét tam giác ABC vuông tại A, ta có \(B{C^2} = A{B^2} + A{C^2}\) (Định lý Pythagore)
Nên \(B{C^2} = {5^2} + {12^2} = 169\) suy ra \(BC = 13\) (cm) .
Theo định nghĩa của tỉ số lượng giác ta có:
\(\sin \widehat B = \frac{{AC}}{{BC}} = \frac{{12}}{{13}};\\\cos \widehat B = \frac{{AB}}{{BC}} = \frac{5}{{13}};\\\tan \widehat B = \frac{{AC}}{{AB}} = \frac{{12}}{5};\\\cot \widehat B = \frac{{AB}}{{AC}} = \frac{5}{{12}}\)
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 69 SGK Toán 9 Kết nối tri thức
Cho tam giác ABC vuông cân tại A và \(AB = AC = a\) (H.4.7a).
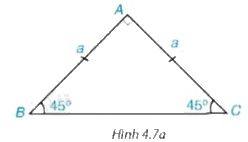
a) Hãy tính BC và các tỉ số \(\frac{{AB}}{{BC}}\) và \(\frac{{AC}}{{BC}}.\) Từ đó suy ra \(\sin {45^0};\cos {45^0}.\)
b) Hãy tính các tỉ số \(\frac{{AB}}{{AC}}\) và \(\frac{{AC}}{{AB}}.\) Từ đó suy ra \(\tan {45^0};\cot {45^0}.\)
Phương pháp giải:
Tính BC theo định lý Pythagore ta có: \(B{C^2} = A{B^2} + A{C^2}\)
Để tính các tỉ số ta thay các độ đo tương ứng của các cạnh.
Lời giải chi tiết:
Tam giác ABC vuông tại A, ta có: \(B{C^2} = A{B^2} + A{C^2}\) (Định lý Pythagore)
Nên \(B{C^2} = {a^2} + {a^2} = 2{a^2}\) suy ra \(BC = a\sqrt 2 \)
a) Tỉ số \(\frac{{AB}}{{BC}} = \frac{a}{{a\sqrt 2 }} = \frac{1}{{\sqrt 2 }} = \frac{{\sqrt 2 }}{2}\) và \(\frac{{AC}}{{BC}} = \frac{a}{{a\sqrt 2 }} = \frac{1}{{\sqrt 2 }} = \frac{{\sqrt 2 }}{2}\).
Do đó \(\sin {45^0} = \sin \widehat B = \frac{{AC}}{{BC}} = \frac{{\sqrt 2 }}{2};\) \(\cos {45^0} = \cos \widehat B = \frac{{AB}}{{BC}} = \frac{{\sqrt 2 }}{2}.\)
b) Tỉ số \(\frac{{AB}}{{AC}} = \frac{a}{a} = 1;\) \(\frac{{AC}}{{AB}} = \frac{a}{a} = 1\)
Do đó \(\tan {45^0} = \tan \widehat B = \frac{{AC}}{{AB}} = 1;\) \(\cot {45^0} = \cot \widehat B = \frac{{AB}}{{AC}} = 1\)
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 3 trang 69 SGK Toán 9 Kết nối tri thức
Xét tam giác đều ABC có cạnh bằng 2a.
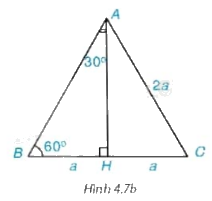
a) Tính đường cao AH của tam giác ABC (H.4.7b) .
b) Tính \(\sin {30^0};\cos {30^0};\sin {60^0};\cos {60^0}.\)
c) Tính \(\tan {30^0};\cot {30^0};\tan {60^0};\cot {60^0}.\)
Phương pháp giải:
Chú ý trong tam giác đều, đường cao vừa là đường phân giác vừa là đường trung tuyến. Từ đó ta tính được cạnh AH và các tỉ số lượng giác liên quan.
Lời giải chi tiết:
a) Tam giác ABC đều có đường cao AH nên AH cũng là đường trung tuyến của tam giác. Do đó ta có H là trung điểm của BC nên \(BH = HC = \frac{{BC}}{2} = \frac{{2a}}{2} = a\)
Xét tam giác ABH vuông tại H, ta có: \(A{B^2} = A{H^2} + H{B^2}\) (Đjnh lý Pythagore)
Suy ra \({\left( {2a} \right)^2} = A{H^2} + {a^2}\) nên \(A{H^2} = 3a\) hay \(AH = a\sqrt 3 \)
b) Tam giác ABC đều nên \(\widehat A = \widehat B = \widehat C = {60^0}\)
Nên \(\cos {60^0} = \cos \widehat B = \frac{{BH}}{{AB}} = \frac{a}{{2a}} = \frac{1}{2};\) \(\sin {60^0} = \sin \widehat B = \frac{{AH}}{{AB}} = \frac{{a\sqrt 3 }}{{2a}} = \frac{{\sqrt 3 }}{2}\)
Tam giác ABC đều nên AH vừa là đường cao vừa là đường phân giác của góc A, do đó \(\widehat {BAH} = \widehat {CAH} = \frac{{\widehat {BAC}}}{2} = \frac{{{{60}^0}}}{2} = {30^0}\)
\(\sin {30^0} = \sin \widehat {BAH} = \frac{{BH}}{{AB}} = \frac{a}{{2a}} = \frac{1}{2};\) \(\cos {30^0} = \cos \widehat {BAH} = \frac{{AH}}{{AB}} = \frac{{a\sqrt 3 }}{{2a}} = \frac{{\sqrt 3 }}{2}\)
c) \(\tan {30^0} = \tan \widehat {BAH} = \frac{{BH}}{{AH}} = \frac{a}{{a\sqrt 3 }} = \frac{{\sqrt 3 }}{3}\)
\(\cot {30^0} = \cot \widehat {BAH} = \frac{{AH}}{{BH}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3 \)
\(\tan {60^0} = \tan \widehat {ABH} = \frac{{AH}}{{BH}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3 \)
\(\cot {60^0} = \tan \widehat {ABH} = \frac{{BH}}{{AH}} = \frac{a}{{a\sqrt 3 }} = \frac{{\sqrt 3 }}{3}\)
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 2 trang 70 SGK Toán 9 Kết nối tri thức
Cho tam giác ABC vuông tại A có \(\widehat C = {45^0}\) và \(AB = c.\) Tính BC và AC theo c.
Phương pháp giải:
Từ công thức lượng giác liên quan đến góc C, ta tính được các cạnh còn lại theo AB.
Tỉ số giữa cạnh đối và cạnh huyền gọi là sin của góc C, kí hiệu \(\sin \widehat C\)
Tỉ số giữa cạnh đối và cạnh kề của góc C gọi là \(\tan \widehat C\)
Lời giải chi tiết:
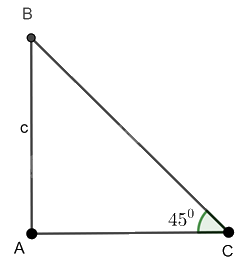
Ta có: \(\tan \widehat C = \frac{{AB}}{{AC}}\) suy ra \(\tan {45^0} = \frac{c}{{AC}}\) do đó \(1 = \frac{c}{{AC}}\) hay \(AC = c\)
\(\sin \widehat C = \frac{{AB}}{{BC}}\) suy ra \(\sin {45^0} = \frac{c}{{BC}}\) do đó \(\frac{{\sqrt 2 }}{2} = \frac{c}{{BC}}\) hay \(BC = \frac{{2c}}{{\sqrt 2 }} = \sqrt 2 c\)
Mục 1 của chương trình Toán 9 tập 1 - Kết nối tri thức tập trung vào việc ôn tập và hệ thống hóa kiến thức về hàm số bậc nhất. Đây là nền tảng quan trọng để học sinh tiếp cận các kiến thức nâng cao hơn trong chương trình. Việc nắm vững các khái niệm, tính chất và phương pháp giải các bài tập liên quan đến hàm số bậc nhất là vô cùng cần thiết.
Bài 1 yêu cầu học sinh xác định các hàm số bậc nhất trong các hàm số đã cho. Để giải bài này, học sinh cần nắm vững định nghĩa của hàm số bậc nhất và kiểm tra xem hàm số có dạng y = ax + b (a ≠ 0) hay không.
Ví dụ: Hàm số y = 2x + 3 là hàm số bậc nhất vì nó có dạng y = ax + b với a = 2 và b = 3.
Bài 2 yêu cầu học sinh vẽ đồ thị của các hàm số bậc nhất đã cho. Để vẽ đồ thị, học sinh cần xác định hai điểm thuộc đồ thị (ví dụ: điểm cắt trục Ox và Oy) và nối chúng lại bằng một đường thẳng.
Ví dụ: Để vẽ đồ thị của hàm số y = -x + 2, ta có thể xác định hai điểm A(0; 2) và B(2; 0) và nối chúng lại bằng một đường thẳng.
Bài 3 yêu cầu học sinh giải các bài toán thực tế liên quan đến hàm số bậc nhất. Để giải bài này, học sinh cần phân tích đề bài, xác định các yếu tố liên quan đến hàm số bậc nhất và lập phương trình để giải.
Ví dụ: Một người đi xe đạp với vận tốc 15 km/h. Quãng đường đi được sau t giờ là bao nhiêu?
Giải: Quãng đường đi được là s = 15t (km). Đây là một hàm số bậc nhất với s là biến số phụ thuộc và t là biến số độc lập.
Khi giải bài tập về hàm số bậc nhất, học sinh cần chú ý các điểm sau:
Việc giải các bài tập trong mục 1 trang 67, 68, 69 SGK Toán 9 tập 1 - Kết nối tri thức là một bước quan trọng trong quá trình học tập môn Toán 9. Hy vọng rằng với những hướng dẫn chi tiết và phương pháp giải bài tập hiệu quả mà giaitoan.edu.vn cung cấp, các em học sinh sẽ tự tin hơn trong việc giải quyết các bài toán về hàm số bậc nhất và đạt kết quả tốt trong học tập.