Chào mừng các em học sinh đến với bài giải bài tập 9.4 trang 71 SGK Toán 9 tập 2 - Kết nối tri thức. Bài tập này thuộc chương trình học Toán 9, tập trung vào việc vận dụng kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Cho đường tròn (O) và hai dây cung AB, CD cắt nhau tại điểm I nằm trong (O) (H.9.9). a) Biết rằng (widehat {AOC} = {60^o},widehat {BOD} = {80^o}). Tính số đo của góc AID. b) Chứng minh rằng (IA.IB = IC.ID).
Đề bài
Cho đường tròn (O) và hai dây cung AB, CD cắt nhau tại điểm I nằm trong (O) (H.9.9).
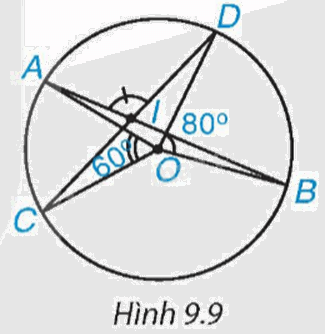
a) Biết rằng \(\widehat {AOC} = {60^o},\widehat {BOD} = {80^o}\). Tính số đo của góc AID.
b) Chứng minh rằng \(IA.IB = IC.ID\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) + Sử dụng mối liên hệ giữa góc nội tiếp và cung bị chắn suy ra: $\widehat{IAC}=\frac{1}{2}sđ\overset\frown{CB},\widehat{ACI}=\frac{1}{2}sđ\overset\frown{AD}$.
+ Sử dụng mối liên hệ giữa góc ở tâm và cung bị chắn suy ra: \(sđ\overset\frown{DB}=\widehat{DOB}={{80}^{o}},sđ\overset\frown{AC}=\widehat{AOC}={{60}^{o}}\).
+ Tính được tổng \(\widehat {IAC} + \widehat {ACI}\).
+ Sử dụng tính chất góc ngoài tam giác tính được: \(\widehat {AID} = \widehat {IAC} + \widehat {ACI}\).
b) Sử dụng mối liên hệ giữa góc nội tiếp và cung bị chắn suy ra \(\widehat {IAD} = \widehat {ICB}\).
Chứng minh $\Delta IAD\backsim \Delta ICB\left( g-g \right)$ suy ra $IA.IB=IC.ID$.
Lời giải chi tiết
a) Xét đường tròn tâm (O) có:
+ Vì góc IAC là góc nội tiếp chắn cung BC nên $\widehat{IAC}=\frac{1}{2}sđ\overset\frown{CB}$.
+ Vì góc ACI là góc nội tiếp chắn cung AD nên $\widehat{ACI}=\frac{1}{2}sđ\overset\frown{AD}$.
+ Vì góc DOB là góc ở tâm chắn cung DB nên \(sđ\overset\frown{DB}=\widehat{DOB}={{80}^{o}}\)
+ Vì góc AOC là góc ở tâm chắn cung AC nên \(sđ\overset\frown{AC}=\widehat{AOC}={{60}^{o}}\)
Ta có: $\widehat{IAC}+\widehat{ACI}=\frac{sđ\overset\frown{CB}+sđ\overset\frown{AD}}{2}=\frac{{{360}^{o}}-sđ\overset\frown{DB}-sđ\overset\frown{AC}}{2}=\frac{{{220}^{o}}}{2}={{110}^{o}}$
Vì góc AID là góc ngoài tại đỉnh I của tam giác AIC nên: \(\widehat {AID} = \widehat {IAC} + \widehat {ACI} = {110^o}\)
b) Vì hai góc nội tiếp IAD và ICB cùng chắn cung DB của đường tròn (O) nên \(\widehat {IAD} = \widehat {ICB}\)
Lại có: \(\widehat {AID} = \widehat {CIB}\) (hai góc đối đỉnh)
Do đó, $\Delta IAD\backsim \Delta ICB\left( g-g \right)$
Suy ra $\frac{IA}{IC}=\frac{ID}{IB}$ nên $ IA.IB=IC.ID$ (đpcm)
Bài tập 9.4 trang 71 SGK Toán 9 tập 2 - Kết nối tri thức yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai để giải quyết một bài toán thực tế liên quan đến quỹ đạo của một vật được ném lên.
Đề bài thường mô tả một tình huống cụ thể, ví dụ như một quả bóng được ném lên từ mặt đất với vận tốc ban đầu nhất định. Yêu cầu của bài toán là xác định độ cao lớn nhất mà quả bóng đạt được, thời gian để quả bóng đạt độ cao lớn nhất, hoặc khoảng cách mà quả bóng bay được trước khi chạm đất.
Để giải bài tập này, chúng ta cần:
Giả sử một quả bóng được ném lên từ mặt đất với vận tốc ban đầu là 15 m/s và góc ném là 60 độ so với phương ngang. Bỏ qua sức cản của không khí. Hãy xác định độ cao lớn nhất mà quả bóng đạt được.
Giải:
Đầu tiên, chúng ta cần phân tích vận tốc ban đầu thành hai thành phần: thành phần ngang và thành phần dọc. Thành phần dọc của vận tốc ban đầu là v0y = v0 * sin(60°) = 15 * sin(60°) ≈ 13 m/s.
Hàm số mô tả độ cao của quả bóng theo thời gian có dạng:
y = -0.5 * g * t2 + v0y * t
Trong đó g là gia tốc trọng trường (g ≈ 9.8 m/s2) và t là thời gian.
Để tìm độ cao lớn nhất, chúng ta cần tìm đỉnh của parabol. Thời gian để quả bóng đạt độ cao lớn nhất là:
t = -b / (2a) = -v0y / (-g) = v0y / g ≈ 13 / 9.8 ≈ 1.33 giây.
Độ cao lớn nhất mà quả bóng đạt được là:
ymax = -0.5 * g * t2 + v0y * t ≈ -0.5 * 9.8 * (1.33)2 + 13 * 1.33 ≈ 8.63 mét.
Để củng cố kiến thức, các em có thể tự giải các bài tập tương tự với các thông số khác nhau. Ví dụ:
Bài tập 9.4 trang 71 SGK Toán 9 tập 2 - Kết nối tri thức là một bài tập quan trọng giúp học sinh hiểu rõ hơn về ứng dụng của hàm số bậc hai trong thực tế. Bằng cách nắm vững phương pháp giải và thực hành giải nhiều bài tập tương tự, các em sẽ tự tin hơn trong quá trình học tập và giải quyết các vấn đề liên quan đến vật lý.
Hy vọng với hướng dẫn chi tiết này, các em sẽ giải bài tập 9.4 trang 71 SGK Toán 9 tập 2 - Kết nối tri thức một cách dễ dàng và hiệu quả. Chúc các em học tốt!