Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 6, 7, 8 sách giáo khoa Toán 9 tập 2 - Kết nối tri thức.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong môn học.
Cho hàm số (y = 2{x^2}). a) Hoàn thành bảng giá trị sau vào vở: b) Trong mặt phẳng Oxy, biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm (left( {x;2{x^2}} right)) với (x in mathbb{R}) và nối lại, ta được đồ thị của hàm số (y = 2{x^2}).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 4 trang 6 SGK Toán 9 Kết nối tri thức
Xét đồ thị của hàm số \(y = 2{x^2}\) đã vẽ ở HĐ3 (H.6.3).
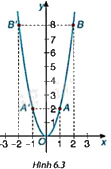
a) Đồ thị nằm về phía trên hay phía dưới trục hoành? Điểm nào là điểm thấp nhất của đồ thị hàm số.
b) So sánh hoành độ và tung độ các cặp điểm thuộc đồ thị: A(1; 2) và \(A'\left( { - 1;2} \right)\); B(2; 8) và \(B'\left( { - 2;8} \right)\).
Từ đó, hãy nhận xét mối liên hệ về vị trí giữa các cặp điểm nêu trên.
c) Tìm điểm C có hoành độ \(x = \frac{1}{2}\) thuộc đồ thị. Xác định tọa độ của điểm C’ đối xứng với điểm C qua trục tung Oy và cho biết điểm C’ có thuộc đồ thị hàm số hay không.
Phương pháp giải:
a, b) Dựa vào đọc đồ thị hàm số để đưa ra nhận xét.
c) + Thay \(x = \frac{1}{2}\) vào hàm số \(y = 2{x^2}\) để tìm y.
+ Sử dụng tính chất: Hai điểm (x; y) và \(\left( { - x;y} \right)\) đối xứng nhau qua trục tung Oy.
Từ đó tìm được tọa độ C’.
+ Thay tọa độ của điểm C’ vào hàm số \(y = 2{x^2}\) để chứng minh điểm C’ thuộc đồ thị hàm số.
Lời giải chi tiết:
a) Đồ thị hàm số nằm phía trên trục hoành. Điểm O (0; 0) là điểm thấp nhất của đồ thị.
b) Hai điểm A(1; 2) và \(A'\left( { - 1;2} \right)\): có hoành độ đối nhau và tung độ bằng nhau.
Hai điểm B(2; 8) và \(B'\left( { - 2;8} \right)\): có hoành độ đối nhau và tung độ bằng nhau.
c) Với \(x = \frac{1}{2}\) thay vào hàm số \(y = 2{x^2}\) thì \(y = 2.{\left( {\frac{1}{2}} \right)^2} = \frac{1}{2}\). Do đó, \(C\left( {\frac{1}{2};\frac{1}{2}} \right)\).
Vì điểm C’ đối xứng với điểm C qua trục Oy nên \(C'\left( { - \frac{1}{2};\frac{1}{2}} \right)\)
Với \(x = - \frac{1}{2}\) thay vào hàm số \(y = 2{x^2}\) ta có: \(2.{\left( { - \frac{1}{2}} \right)^2} = \frac{1}{2} = {y_{C'}}\)
Do đó, điểm \(C'\left( { - \frac{1}{2};\frac{1}{2}} \right)\) thuộc đồ thị hàm số \(y = 2{x^2}\).
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 2 trang 8SGK Toán 9 Kết nối tri thức
Vẽ đồ thị của hàm số \(y = \frac{1}{2}{x^2}\). Tìm các điểm thuộc đồ thị có tung độ bằng 2 và nhận xét về tính đối xứng giữa các điểm đó.
Phương pháp giải:
Cách vẽ đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\):
+ Lập bảng ghi một số cặp giá trị tương ứng của x và y.
+ Trong mặt phẳng tọa độ Oxy, biểu diễn các cặp điểm (x; y) trong bảng giá trị trên và nối chúng lại để được một đường cong là đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\).
Lời giải chi tiết:
Lập bảng một số cặp giá trị tương ứng của x và y:

Biểu diễn các điểm \(\left( { - 4;8} \right),\left( { - 2;2} \right);\left( { - 1;\frac{1}{2}} \right);\left( {0;0} \right);\left( {4;8} \right),\left( {2;2} \right);\left( {1;\frac{1}{2}} \right)\) trên mặt phẳng tọa độ Oxy và nối chúng lại ta được đồ thị hàm số \(y = \frac{1}{2}{x^2}\) như hình vẽ.
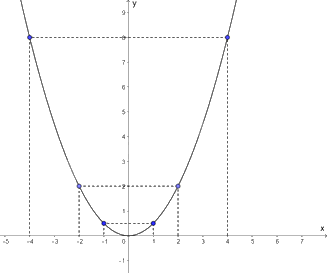
Các điểm thuộc đồ thị hàm số có tung độ bằng 2 là \(\left( { - 2;2} \right)\) và \(\left( {2;2} \right)\). Hai điểm này đối xứng với nhau qua trục Oy.
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 2 trang 8 SGK Toán 9 Kết nối tri thức
Giải quyết bài toán ở tình huống mở đầu.
Tình huống mở đầu
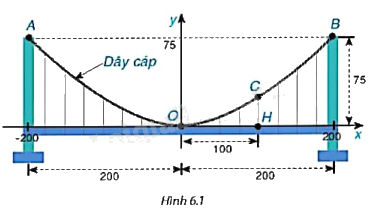
Một cây cầu treo có trụ tháp đôi cao 75m so với mặt của cây cầu và cách nhau 400m. Các dây cáp có dạng đồ thị của hàm số \(y = ax^2 (a \ne 0)\) như Hình 6.1 và được treo trên các đỉnh tháp. Tính chiều cao CH của dây cáp biết điểm H cách tâm O của cây cầu 100m (giả sử mặt của cây cầu là bằng phẳng).
Phương pháp giải:
+ Thay điểm (200; 75) vào hàm số \(y = a{x^2}\) ta tìm được a. Viết lại hàm số đã tìm được.
+ Thay \(x = 100\) vào hàm số đã tìm được ta tính được y, giá trị y chính là chiều cao của cây cầu.
Lời giải chi tiết:
Đồ thị hàm số \(y = a{x^2}\) đi qua điểm (200; 75) nên ta có: \(75 = a{.200^2} \Rightarrow a = \frac{3}{{1600}}\).
Khi đó, \(y = \frac{3}{{1600}}{x^2}\).
Với \(x = 100\) ta có: \(y = \frac{3}{{1600}}{.100^2} = \frac{{75}}{4}\).
Vậy chiều cao \(CH = \frac{{75}}{4}m\) khi điểm H cách tâm O của cây cầu 100m.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 3 trang 6 SGK Toán 9 Kết nối tri thức
Cho hàm số \(y = 2{x^2}\).
a) Hoàn thành bảng giá trị sau vào vở:

b) Trong mặt phẳng Oxy, biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm \(\left( {x;2{x^2}} \right)\) với \(x \in \mathbb{R}\) và nối lại, ta được đồ thị của hàm số \(y = 2{x^2}\).
Phương pháp giải:
a) Thay lần lượt các giá trị \(x = - 3;x = - 2;x = - 1;x = 0;x = 1;x = 2;x = 3\) vào hàm số \(y = 2{x^2}\) ta sẽ tìm được y tương ứng, từ đó hoàn thành được bảng.
b) Cách biểu diễn điểm \(A\left( {{x_0};{y_0}} \right)\) trên mặt phẳng tọa độ Oxy:
+ Dựng đường thẳng vuông góc với trục Ox tại \({x_0}\).
+ Dựng đường thẳng vuông góc với trục Oy tại \({y_0}\).
+ Hai đường thẳng vừa dựng trên cắt nhau tại A.
Khi đó, ta đã biểu diễn được điểm \(A\left( {{x_0};{y_0}} \right)\) trên mặt phẳng tọa độ Oxy.
Lời giải chi tiết:
a)

b) Biểu diễn các điểm \(\left( { - 3;18} \right);\left( { - 2;8} \right);\left( { - 1;2} \right);\left( {0;0} \right);\left( {3;18} \right);\left( {2;8} \right);\left( {1;2} \right)\) trên mặt phẳng tọa độ Oxy ta được:
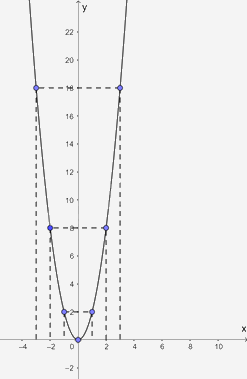
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 3 trang 6 SGK Toán 9 Kết nối tri thức
Cho hàm số \(y = 2{x^2}\).
a) Hoàn thành bảng giá trị sau vào vở:

b) Trong mặt phẳng Oxy, biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm \(\left( {x;2{x^2}} \right)\) với \(x \in \mathbb{R}\) và nối lại, ta được đồ thị của hàm số \(y = 2{x^2}\).
Phương pháp giải:
a) Thay lần lượt các giá trị \(x = - 3;x = - 2;x = - 1;x = 0;x = 1;x = 2;x = 3\) vào hàm số \(y = 2{x^2}\) ta sẽ tìm được y tương ứng, từ đó hoàn thành được bảng.
b) Cách biểu diễn điểm \(A\left( {{x_0};{y_0}} \right)\) trên mặt phẳng tọa độ Oxy:
+ Dựng đường thẳng vuông góc với trục Ox tại \({x_0}\).
+ Dựng đường thẳng vuông góc với trục Oy tại \({y_0}\).
+ Hai đường thẳng vừa dựng trên cắt nhau tại A.
Khi đó, ta đã biểu diễn được điểm \(A\left( {{x_0};{y_0}} \right)\) trên mặt phẳng tọa độ Oxy.
Lời giải chi tiết:
a)

b) Biểu diễn các điểm \(\left( { - 3;18} \right);\left( { - 2;8} \right);\left( { - 1;2} \right);\left( {0;0} \right);\left( {3;18} \right);\left( {2;8} \right);\left( {1;2} \right)\) trên mặt phẳng tọa độ Oxy ta được:
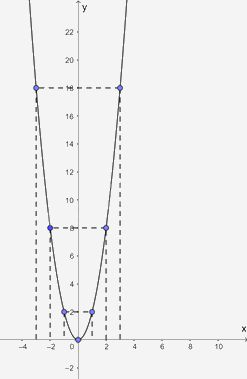
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 4 trang 6 SGK Toán 9 Kết nối tri thức
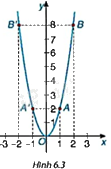
Xét đồ thị của hàm số \(y = 2{x^2}\) đã vẽ ở HĐ3 (H.6.3).
a) Đồ thị nằm về phía trên hay phía dưới trục hoành? Điểm nào là điểm thấp nhất của đồ thị hàm số.
b) So sánh hoành độ và tung độ các cặp điểm thuộc đồ thị: A(1; 2) và \(A'\left( { - 1;2} \right)\); B(2; 8) và \(B'\left( { - 2;8} \right)\).
Từ đó, hãy nhận xét mối liên hệ về vị trí giữa các cặp điểm nêu trên.
c) Tìm điểm C có hoành độ \(x = \frac{1}{2}\) thuộc đồ thị. Xác định tọa độ của điểm C’ đối xứng với điểm C qua trục tung Oy và cho biết điểm C’ có thuộc đồ thị hàm số hay không.
Phương pháp giải:
a, b) Dựa vào đọc đồ thị hàm số để đưa ra nhận xét.
c) + Thay \(x = \frac{1}{2}\) vào hàm số \(y = 2{x^2}\) để tìm y.
+ Sử dụng tính chất: Hai điểm (x; y) và \(\left( { - x;y} \right)\) đối xứng nhau qua trục tung Oy.
Từ đó tìm được tọa độ C’.
+ Thay tọa độ của điểm C’ vào hàm số \(y = 2{x^2}\) để chứng minh điểm C’ thuộc đồ thị hàm số.
Lời giải chi tiết:
a) Đồ thị hàm số nằm phía trên trục hoành. Điểm O (0; 0) là điểm thấp nhất của đồ thị.
b) Hai điểm A(1; 2) và \(A'\left( { - 1;2} \right)\): có hoành độ đối nhau và tung độ bằng nhau.
Hai điểm B(2; 8) và \(B'\left( { - 2;8} \right)\): có hoành độ đối nhau và tung độ bằng nhau.
c) Với \(x = \frac{1}{2}\) thay vào hàm số \(y = 2{x^2}\) thì \(y = 2.{\left( {\frac{1}{2}} \right)^2} = \frac{1}{2}\). Do đó, \(C\left( {\frac{1}{2};\frac{1}{2}} \right)\).
Vì điểm C’ đối xứng với điểm C qua trục Oy nên \(C'\left( { - \frac{1}{2};\frac{1}{2}} \right)\)
Với \(x = - \frac{1}{2}\) thay vào hàm số \(y = 2{x^2}\) ta có: \(2.{\left( { - \frac{1}{2}} \right)^2} = \frac{1}{2} = {y_{C'}}\)
Do đó, điểm \(C'\left( { - \frac{1}{2};\frac{1}{2}} \right)\) thuộc đồ thị hàm số \(y = 2{x^2}\).
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 2 trang 8SGK Toán 9 Kết nối tri thức
Vẽ đồ thị của hàm số \(y = \frac{1}{2}{x^2}\). Tìm các điểm thuộc đồ thị có tung độ bằng 2 và nhận xét về tính đối xứng giữa các điểm đó.
Phương pháp giải:
Cách vẽ đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\):
+ Lập bảng ghi một số cặp giá trị tương ứng của x và y.
+ Trong mặt phẳng tọa độ Oxy, biểu diễn các cặp điểm (x; y) trong bảng giá trị trên và nối chúng lại để được một đường cong là đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\).
Lời giải chi tiết:
Lập bảng một số cặp giá trị tương ứng của x và y:

Biểu diễn các điểm \(\left( { - 4;8} \right),\left( { - 2;2} \right);\left( { - 1;\frac{1}{2}} \right);\left( {0;0} \right);\left( {4;8} \right),\left( {2;2} \right);\left( {1;\frac{1}{2}} \right)\) trên mặt phẳng tọa độ Oxy và nối chúng lại ta được đồ thị hàm số \(y = \frac{1}{2}{x^2}\) như hình vẽ.
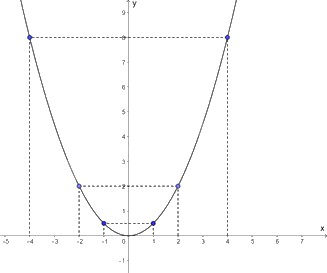
Các điểm thuộc đồ thị hàm số có tung độ bằng 2 là \(\left( { - 2;2} \right)\) và \(\left( {2;2} \right)\). Hai điểm này đối xứng với nhau qua trục Oy.
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 2 trang 8 SGK Toán 9 Kết nối tri thức
Giải quyết bài toán ở tình huống mở đầu.
Tình huống mở đầu
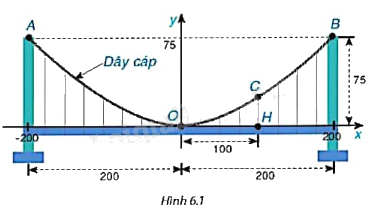
Một cây cầu treo có trụ tháp đôi cao 75m so với mặt của cây cầu và cách nhau 400m. Các dây cáp có dạng đồ thị của hàm số \(y = ax^2 (a \ne 0)\) như Hình 6.1 và được treo trên các đỉnh tháp. Tính chiều cao CH của dây cáp biết điểm H cách tâm O của cây cầu 100m (giả sử mặt của cây cầu là bằng phẳng).
Phương pháp giải:
+ Thay điểm (200; 75) vào hàm số \(y = a{x^2}\) ta tìm được a. Viết lại hàm số đã tìm được.
+ Thay \(x = 100\) vào hàm số đã tìm được ta tính được y, giá trị y chính là chiều cao của cây cầu.
Lời giải chi tiết:
Đồ thị hàm số \(y = a{x^2}\) đi qua điểm (200; 75) nên ta có: \(75 = a{.200^2} \Rightarrow a = \frac{3}{{1600}}\).
Khi đó, \(y = \frac{3}{{1600}}{x^2}\).
Với \(x = 100\) ta có: \(y = \frac{3}{{1600}}{.100^2} = \frac{{75}}{4}\).
Vậy chiều cao \(CH = \frac{{75}}{4}m\) khi điểm H cách tâm O của cây cầu 100m.
Mục 2 của chương trình Toán 9 tập 2 - Kết nối tri thức tập trung vào việc ôn tập và hệ thống hóa kiến thức về hàm số bậc hai. Các bài tập trong mục này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, đồng thời rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Bài tập này yêu cầu học sinh nhắc lại các kiến thức cơ bản về hàm số bậc hai, bao gồm:
Để giải bài tập này, học sinh cần nắm vững các định nghĩa và tính chất của hàm số bậc hai, đồng thời biết cách áp dụng chúng vào việc giải quyết các bài toán cụ thể.
Bài tập này yêu cầu học sinh tìm tập xác định của các hàm số được cho. Để giải bài tập này, học sinh cần hiểu rõ khái niệm tập xác định của hàm số và biết cách xác định các điều kiện để hàm số có nghĩa.
Ví dụ, với hàm số y = √(x - 2), tập xác định là x ≥ 2.
Bài tập này yêu cầu học sinh xác định hệ số a, b, c của các hàm số bậc hai được cho. Để giải bài tập này, học sinh cần biết cách nhận dạng dạng tổng quát của hàm số bậc hai và so sánh với hàm số đã cho để xác định các hệ số tương ứng.
Ví dụ, với hàm số y = 2x2 - 3x + 1, ta có a = 2, b = -3, c = 1.
Bài tập này yêu cầu học sinh vẽ đồ thị của các hàm số bậc hai được cho. Để giải bài tập này, học sinh cần xác định các yếu tố của parabol (đỉnh, trục đối xứng, tiêu điểm, đường chuẩn) và sử dụng chúng để vẽ đồ thị.
Có thể sử dụng phần mềm vẽ đồ thị hoặc vẽ bằng tay.
Khi giải bài tập về hàm số bậc hai, học sinh cần lưu ý một số điểm sau:
Hy vọng với những hướng dẫn chi tiết và phương pháp giải bài tập hiệu quả trên đây, các em học sinh sẽ tự tin hơn trong việc giải các bài tập trong mục 2 trang 6, 7, 8 SGK Toán 9 tập 2 - Kết nối tri thức. Chúc các em học tập tốt!