Bài tập 3.24 trang 62 SGK Toán 9 tập 1 thuộc chương 3: Hệ hai phương trình tuyến tính. Bài tập này yêu cầu học sinh vận dụng kiến thức về phương pháp giải hệ phương trình để tìm nghiệm của hệ phương trình đã cho.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 3.24, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Sử dụng MTCT, tính các căn bậc ba sau đây (làm tròn kết quả đến chữ số thập phân thứ hai) : a) (sqrt[3]{{2,1}};) b) (sqrt[3]{{ - 18}};) c) (sqrt[3]{{ - 28}};) d) (sqrt[3]{{0,35}}.)
Đề bài
Sử dụng MTCT, tính các căn bậc ba sau đây (làm tròn kết quả đến chữ số thập phân thứ hai) :
a) \(\sqrt[3]{{2,1}};\)
b) \(\sqrt[3]{{ - 18}};\)
c) \(\sqrt[3]{{ - 28}};\)
d) \(\sqrt[3]{{0,35}}.\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng MTCT ta bấm được kết quả, chú ý quy tắc làm tròn (Nếu số đứng liền sau số có nghĩa mà lớn hơn hoặc bằng 5 thì số có nghĩa cuối cùng được cộng thêm 1, trường hợp ngược lại ta giữ nguyên số đã cho đến số có nghĩa cuối cùng cần làm tròn).
Lời giải chi tiết
a)
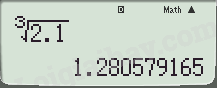
\(\sqrt[3]{{2,1}} \approx 1,28\)
b)
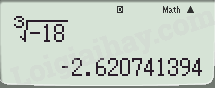
\(\sqrt[3]{{ - 18}} \approx - 2,62\)
c)
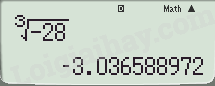
\(\sqrt[3]{{ - 28}} \approx - 3,04\)
d)
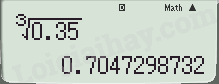
\(\sqrt[3]{{0,35}} \approx 0,70\)
Bài tập 3.24 SGK Toán 9 tập 1 - Kết nối tri thức là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về hệ phương trình tuyến tính. Để giải bài tập này, chúng ta cần nắm vững các phương pháp giải hệ phương trình như phương pháp thế, phương pháp cộng đại số và phương pháp đồ thị.
Giải các hệ phương trình sau:
a) {x + y = 5
2x - y = 1
b) {3x - 2y = 7
x + 2y = 3
c) {x - 2y = -1
3x + y = 5
d) {2x + 3y = 8
x - y = 1
a) Giải hệ phương trình:
{x + y = 5
2x - y = 1
Phương pháp cộng đại số: Cộng hai phương trình vế với vế, ta được:
x + y + 2x - y = 5 + 1
3x = 6
x = 2
Thay x = 2 vào phương trình x + y = 5, ta được:
2 + y = 5
y = 3
Vậy nghiệm của hệ phương trình là x = 2, y = 3
b) Giải hệ phương trình:
{3x - 2y = 7
x + 2y = 3
Phương pháp cộng đại số: Cộng hai phương trình vế với vế, ta được:
3x - 2y + x + 2y = 7 + 3
4x = 10
x = 2.5
Thay x = 2.5 vào phương trình x + 2y = 3, ta được:
2.5 + 2y = 3
2y = 0.5
y = 0.25
Vậy nghiệm của hệ phương trình là x = 2.5, y = 0.25
(Các phần c và d sẽ được giải tương tự như trên, sử dụng phương pháp cộng đại số hoặc phương pháp thế tùy thuộc vào từng hệ phương trình)
Hệ phương trình tuyến tính có rất nhiều ứng dụng trong thực tế, ví dụ như:
Hy vọng với lời giải chi tiết này, các em học sinh sẽ hiểu rõ hơn về cách giải bài tập 3.24 trang 62 SGK Toán 9 tập 1 - Kết nối tri thức và tự tin hơn trong các kỳ thi.