Bài học này cung cấp lý thuyết đầy đủ và chi tiết về cách biến đổi đơn giản và rút gọn các biểu thức chứa căn thức bậc hai trong chương trình Toán 9 Kết nối tri thức.
Chúng ta sẽ cùng nhau tìm hiểu các quy tắc, tính chất quan trọng và áp dụng chúng vào giải các bài tập thực tế.
Mục tiêu là giúp các em học sinh nắm vững kiến thức nền tảng và tự tin giải quyết các bài toán liên quan đến căn thức bậc hai.
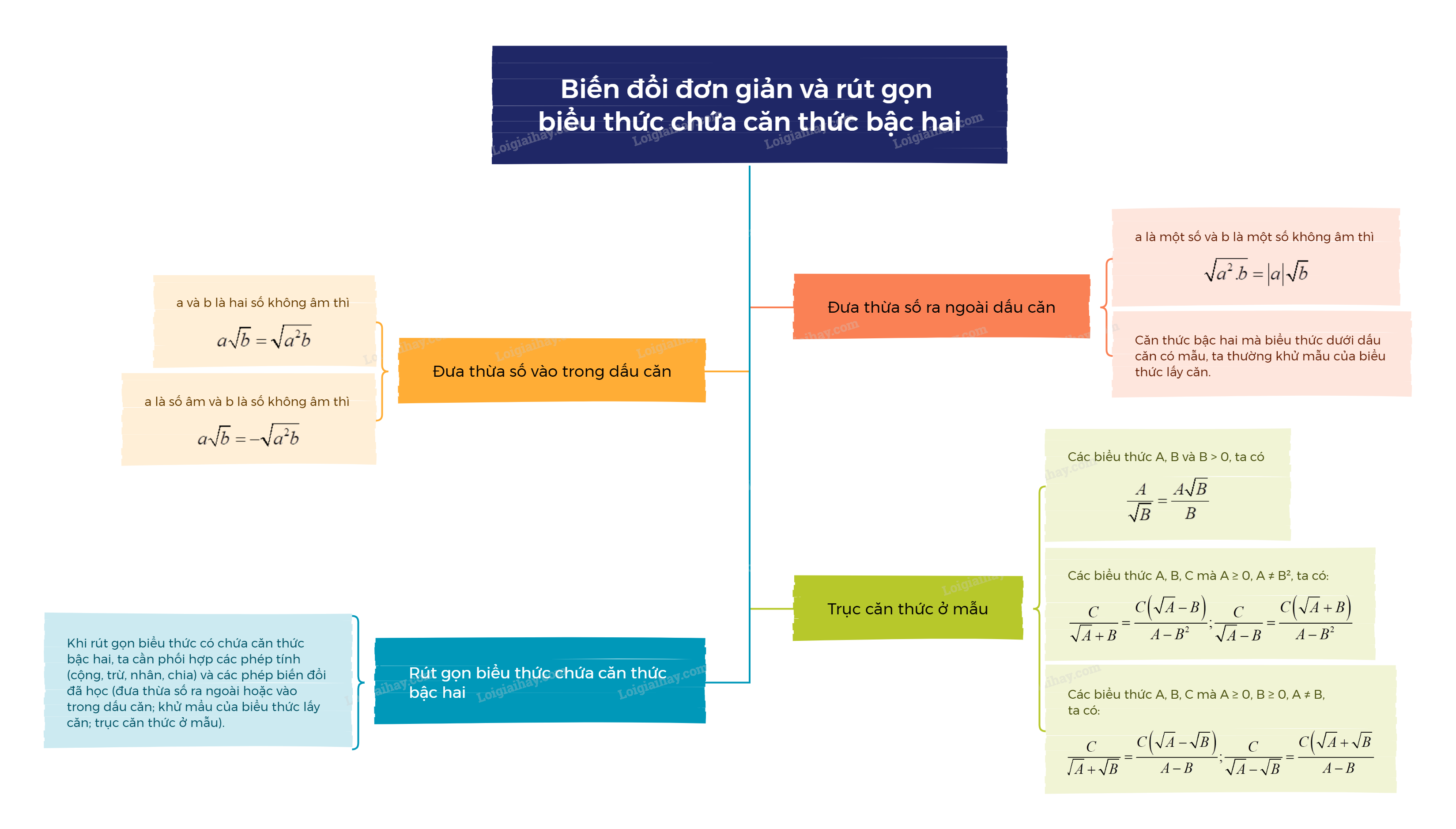
1. Đưa thừa số ra ngoài dấu căn Phép đưa thừa số ra ngoài dấu căn
1. Đưa thừa số ra ngoài dấu căn
Phép đưa thừa số ra ngoài dấu căn
Nếu a là một số và b là một số không âm thì \(\sqrt {{a^2}.b} = \left| a \right|\sqrt b \). |
Ví dụ:
\(\sqrt {45} = \sqrt {{3^2}.5} = 3\sqrt 5 \);
\(\sqrt {243a} = \sqrt {{9^2}.3a} = 9\sqrt {3a} \).
Với những căn thức bậc hai mà biểu thức dưới dấu căn có mẫu, ta thường khử mẫu của biểu thức lấy căn (biến đổi căn thức bậc hai đó thành một biểu thức mà trong căn thức không còn mẫu). |
Ví dụ: \(\sqrt {\frac{4}{7}} = \sqrt {\frac{{4.7}}{{{7^2}}}} = \sqrt {{{\left( {\frac{2}{7}} \right)}^2}.7} = \frac{{2\sqrt 7 }}{7}\).
2. Đưa thừa số vào trong dấu căn
Phép đưa thừa số vào trong dấu căn
- Nếu a và b là hai số không âm thì \(a\sqrt b = \sqrt {{a^2}b} \). - Nếu a là số âm và b là số không âm thì \(a\sqrt b = - \sqrt {{a^2}b} \). |
Ví dụ:
\(5\sqrt 2 = \sqrt {{5^2}.2} = \sqrt {50} \);
Với \(a \ge 0\) thì \( - 2\sqrt a = - \sqrt {{2^2}.a} = - \sqrt {4a} \).
3. Trục căn thức ở mẫu
Cách trục căn thức ở mẫu
- Với các biểu thức A, B và B > 0, ta có \(\frac{A}{{\sqrt B }} = \frac{{A\sqrt B }}{B}\). - Với các biểu thức A, B, C mà \(A \ge 0,A \ne {B^2}\), ta có: \(\frac{C}{{\sqrt A + B}} = \frac{{C\left( {\sqrt A - B} \right)}}{{A - {B^2}}};\frac{C}{{\sqrt A - B}} = \frac{{C\left( {\sqrt A + B} \right)}}{{A - {B^2}}}\). - Với các biểu thức A, B, C mà \(A \ge 0,B \ge 0,A \ne B\), ta có: \(\frac{C}{{\sqrt A + \sqrt B }} = \frac{{C\left( {\sqrt A - \sqrt B } \right)}}{{A - B}};\frac{C}{{\sqrt A - \sqrt B }} = \frac{{C\left( {\sqrt A + \sqrt B } \right)}}{{A - B}}\). |
Ví dụ:
\(\frac{2}{{3\sqrt 5 }} = \frac{{2\sqrt 5 }}{{3{{\left( {\sqrt 5 } \right)}^2}}} = \frac{{2\sqrt 5 }}{{3.5}} = \frac{{2\sqrt 5 }}{{15}}\);
\(\frac{a}{{3 - 2\sqrt 2 }} = \frac{{a\left( {3 + 2\sqrt 2 } \right)}}{{\left( {3 - 2\sqrt 2 } \right).\left( {3 + 2\sqrt 2 } \right)}} = \frac{{a\left( {3 + 2\sqrt 2 } \right)}}{{{3^2} - {{\left( {2\sqrt 2 } \right)}^2}}} = \frac{{a\left( {3 + 2\sqrt 2 } \right)}}{{9 - 8}} = \left( {3 + 2\sqrt 2 } \right)a\).
4. Rút gọn biểu thức chứa căn thức bậc hai
Khi rút gọn biểu thức có chứa căn thức bậc hai, ta cần phối hợp các phép tính (cộng, trừ, nhân, chia) và các phép biến đổi đã học (đưa thừa số ra ngoài hoặc vào trong dấu căn; khử mẩu của biểu thức lấy căn; trục căn thức ở mẫu). |
Ví dụ:
\(\begin{array}{l}A = 2\sqrt 3 - \sqrt {75} + \sqrt {{{\left( {1 - \sqrt 3 } \right)}^2}} \\ = 2\sqrt 3 - \sqrt {{{3.5}^2}} + \left| {1 - \sqrt 3 } \right|\\ = 2\sqrt 3 - 5\sqrt 3 + \sqrt 3 - 1\\ = - 1 - 2\sqrt 3 \end{array}\)
\(\begin{array}{l}B = x\sqrt x - \frac{{{x^2} - x}}{{\sqrt x + 1}}\\ = x\sqrt x - \frac{{\left( {{x^2} - x} \right)\left( {\sqrt x - 1} \right)}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}\\ = x\sqrt x - \frac{{x\left( {x - 1} \right)\left( {\sqrt x - 1} \right)}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}\\ = x\sqrt x - \frac{{x\left( {x - 1} \right)\left( {\sqrt x - 1} \right)}}{{x - 1}}\\ = x\sqrt x - x\left( {\sqrt x - 1} \right)\\ = x\sqrt x - x\sqrt x + x\\ = x\end{array}\)
Căn thức bậc hai là một phần quan trọng trong chương trình Toán 9, đặc biệt là chương trình Kết nối tri thức. Việc nắm vững lý thuyết và kỹ năng biến đổi, rút gọn biểu thức chứa căn thức bậc hai là nền tảng để giải quyết các bài toán phức tạp hơn trong các chương trình học tiếp theo.
Căn thức bậc hai của một số thực a (với a ≥ 0) là số x sao cho x2 = a. Ký hiệu: √a. Trong đó:
Căn thức bậc hai √a chỉ xác định khi và chỉ khi a ≥ 0.
Để rút gọn biểu thức chứa căn thức bậc hai, ta thực hiện các bước sau:
Ví dụ 1: Rút gọn biểu thức √75
Giải:
√75 = √(25 * 3) = √25 * √3 = 5√3
Ví dụ 2: Rút gọn biểu thức √(16x2) với x < 0
Giải:
√(16x2) = √((4x)2) = |4x| = -4x (vì x < 0)
Hãy tự luyện tập với các bài tập sau để củng cố kiến thức:
Việc nắm vững lý thuyết và kỹ năng biến đổi, rút gọn biểu thức chứa căn thức bậc hai là rất quan trọng trong chương trình Toán 9. Hy vọng bài học này đã cung cấp cho các em những kiến thức cần thiết và giúp các em tự tin hơn trong việc giải các bài toán liên quan đến căn thức bậc hai.