Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9 tập 2 - Kết nối tri thức. Bài viết này sẽ hướng dẫn bạn từng bước giải bài tập 10 trang 128, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải một cách cẩn thận, đảm bảo tính chính xác và dễ tiếp thu.
Cho tam giác ABC vuông tại B có góc (widehat A = {30^o},AB = 6cm). Vẽ tia Bt sao cho (widehat {tBC} = {30^o}), cắt tia AC ở D (C nằm giữa A và D). a) Chứng minh tam giác ABD cân tại B. b) Tính khoảng cách từ D đến đường thẳng AB.
Đề bài
Cho tam giác ABC vuông tại B có góc \(\widehat A = {30^o},AB = 6cm\). Vẽ tia Bt sao cho \(\widehat {tBC} = {30^o}\), cắt tia AC ở D (C nằm giữa A và D).
a) Chứng minh tam giác ABD cân tại B.
b) Tính khoảng cách từ D đến đường thẳng AB.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) + Tính được \(\widehat {DBA} = \widehat {DBC} + \widehat {CBA} = {120^o}\).
+ Tính được \(\widehat {BDA} = {30^o}\) nên tam giác ABD cân tại B.
b) + \(BD = AB = 6cm\).
+ Kẻ DE vuông góc với AB tại E. Khi đó, DE là khoảng cách từ D đến đường thẳng AB.
+ \(\widehat {DBE} = {180^o} - \widehat {DBA} = {60^o}\).
+ Tam giác BED vuông tại E nên \(ED = BD.\sin \widehat {DBE}\).
Lời giải chi tiết
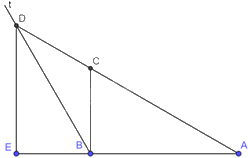
a) \(\Delta \)ABC vuông tại B nên \(\widehat {CBA} = {90^o}\). Ta có: \(\widehat {DBA} = \widehat {DBC} + \widehat {CBA} = {30^o} + {90^o} = {120^o}\)
\(\Delta \)DBA có: \(\widehat {BDA} = {180^o} - \widehat {DBA} - \widehat A = {180^o} - {120^o} - {30^o} = {30^o}\). Do đó, \(\widehat {BDA} = \widehat A\) nên \(\Delta \)ABD cân tại B.
b) Vì \(\Delta \)ABD cân tại B nên \(BD = AB = 6cm\).
Kẻ DE vuông góc với AB tại E. Khi đó, DE là khoảng cách từ D đến đường thẳng AB.
Ta có: \(\widehat {DBE} = {180^o} - \widehat {DBA} = {180^o} - {120^o} = {60^o}\).
\(\Delta \)BED vuông tại E nên \(ED = BD.\sin \widehat {DBE} = 6.\sin {60^o} = 6.\frac{{\sqrt 3 }}{2} = 3\sqrt 3 \left( {cm} \right)\)
Vậy khoảng cách từ D đến đường thẳng AB bằng \(3\sqrt 3 \)cm.
Bài tập 10 trang 128 SGK Toán 9 tập 2 - Kết nối tri thức thuộc chương trình học về hàm số bậc hai. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về:
Trước khi bắt tay vào giải bài tập, điều quan trọng là phải đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Bài tập 10 trang 128 thường yêu cầu học sinh:
Để minh họa, chúng ta sẽ cùng giải một ví dụ cụ thể. Giả sử bài tập yêu cầu chúng ta xét hàm số y = 2x2 - 4x + 1.
Trong hàm số y = 2x2 - 4x + 1, ta có:
Tọa độ đỉnh của parabol có dạng (x0; y0), trong đó:
Vậy, tọa độ đỉnh của parabol là (1; -1).
Để vẽ đồ thị của hàm số, ta cần xác định thêm một vài điểm thuộc đồ thị. Ví dụ:
| x | y |
|---|---|
| 0 | 1 |
| 2 | 1 |
| -1 | 7 |
Dựa vào các điểm này và tọa độ đỉnh, ta có thể vẽ được đồ thị của hàm số.
Tùy thuộc vào yêu cầu cụ thể của bài toán, ta có thể sử dụng kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế, chẳng hạn như tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của một biểu thức, hoặc tìm quỹ đạo của một vật thể chuyển động.
Để giải bài tập về hàm số bậc hai một cách hiệu quả, bạn cần:
Bài tập 10 trang 128 SGK Toán 9 tập 2 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc hai. Hy vọng rằng với hướng dẫn chi tiết này, bạn sẽ tự tin hơn trong việc giải bài tập và đạt kết quả tốt trong môn Toán.
Giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục tri thức. Hãy truy cập website của chúng tôi để tìm hiểu thêm về các bài giải Toán 9 khác và các tài liệu học tập hữu ích.