Bài tập 2.30 trang 42 SGK Toán 9 tập 1 thuộc chương Hàm số bậc nhất. Đây là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng vận dụng kiến thức về hàm số bậc nhất vào giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 2.30 này, giúp các em học sinh hiểu rõ phương pháp giải và tự tin hơn khi làm bài tập.
Một hãng viễn thông nước ngoài có hai gói cước như sau: a) Hãy viết một phương trình xác định thời gian gọi (phút) mà phí phải trả trong cùng một tháng của hai gói cước là như nhau và giải phương trình đó. b) Nếu khách hàng chỉ gọi tối đa là 180 phút trong 1 tháng thì nên dùng gói cước nào? Nếu khách hàng gọi 500 phút trong 1 tháng thì nên dùng gói cước nào?
Đề bài
Một hãng viễn thông nước ngoài có hai gói cước như sau:
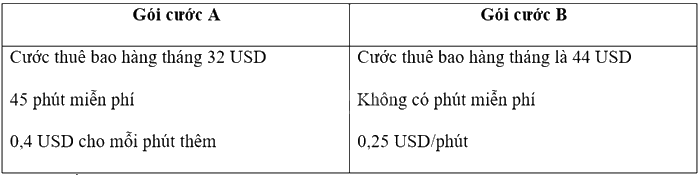
a) Hãy viết một phương trình xác định thời gian gọi (phút) mà phí phải trả trong cùng một tháng của hai gói cước là như nhau và giải phương trình đó.
b) Nếu khách hàng chỉ gọi tối đa là 180 phút trong 1 tháng thì nên dùng gói cước nào? Nếu khách hàng gọi 500 phút trong 1 tháng thì nên dùng gói cước nào?
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Gọi thời gian gọi là x (phút) \(\left( {x > 0} \right)\)
Biểu diễn số tiền phải trả khi gọi x phút đối với gói cước A, B. (Đối với gói cước A có 2 trường hợp:
\(TH1:x \le 45\)
\(TH2:x > 45\)
Xác định phương trình cần tìm và giải.
b) Ta cần tính số chi phí phải trả khi dùng cả hai gói cước, từ đó ta có lựa chọn gói cước cho phù hợp.
Lời giải chi tiết
a) Gọi thời gian gọi trong một tháng là x (phút) \(\left( {x > 0} \right)\)
Số tiền phải trả khi gọi x phút đối với gói cước B là \(44 + 0,25.x\) (USD)
Số tiền phải trả khi x phút đối với gói cước A là
\(TH1:x \le 45\) thì phí trả là 32 USD.
\(TH2:x > 45\) thì phí trả là \(32 + 0,4.\left( {x - 45} \right)\)
Vì số tiền phải trả của gói cước B lớn hơn 44 nên để phí trả hai gói cước trong cùng một tháng của hai gói cước là như nhau thì đối với gói cước A thì sẽ rơi vào trường hợp thứ hai nên ta có phương trình:
\(44 + 0,25.x = 32 + \left( {x - 45} \right).0,4\)
\(0,25.x - 0,4x = - 44 + 32 - 45.0,4\)
\( - 0,15x = - 30\)
\(x = 200\left( {t/m} \right).\)
Vậy khi gọi 200 phút thì chi phí phải trả đối với hai gói cước là như nhau.
b) Ta có bất phương trình biểu thị thời gian gọi mà chi phí gói cước A lớn hơn gói cước B là:
\(\begin{array}{l}32 + \left( {x - 45} \right).0,4 > 44 + 0,25x\\32 + 0,4x - 18 > 44 + 0,25x\\0,4x - 0,25x > 44 - 32 + 18\\0,15x > 30\\x > 200\end{array}\)
Suy ra với thời gian gọi lớn hơn 200 phút thì chi phí phải trả theo gói cước A lớn hơn chi phí phải trả theo gói cước B.
Vậy nếu khách hàng chỉ dùng tối đa 180 phút (< 200) trong một tháng thì nên dùng gói cước A;
nếu khách hàng dùng khoảng 500 phút (> 200) trong một tháng thì nên dùng gói cước B.
Bài tập 2.30 trang 42 SGK Toán 9 tập 1 - Kết nối tri thức yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết một bài toán thực tế liên quan đến việc xác định hàm số và tính giá trị của hàm số tại một điểm cho trước.
Đề bài: (Nội dung đề bài đầy đủ của bài tập 2.30)
Lời giải:
(Lời giải chi tiết, từng bước, có giải thích rõ ràng)
Để hiểu rõ hơn về cách giải bài tập này, chúng ta hãy xem xét một ví dụ minh họa:
(Ví dụ minh họa với số liệu cụ thể và lời giải chi tiết)
Để rèn luyện thêm kỹ năng giải bài tập về hàm số bậc nhất, các em có thể tham khảo các bài tập tương tự sau:
Khi giải bài tập về hàm số bậc nhất, các em cần lưu ý những điều sau:
Bài tập 2.30 trang 42 SGK Toán 9 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng vận dụng kiến thức về hàm số bậc nhất. Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, các em học sinh sẽ hiểu rõ hơn về cách giải bài tập này và tự tin hơn khi làm bài tập.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!