Bài tập 9.22 trang 83 SGK Toán 9 tập 2 thuộc chương trình Toán 9 Kết nối tri thức, yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế. Bài viết này sẽ cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Giaitoan.edu.vn luôn đồng hành cùng các em học sinh trên con đường chinh phục môn Toán. Chúng tôi cung cấp đầy đủ các bài giải SGK Toán 9, bài tập trắc nghiệm, và các tài liệu học tập hữu ích khác.
Tính diện tích của một hình chữ nhật, biết rằng hình chữ nhật đó có chiều dài gấp hai lần chiều rộng và bán kính đường tròn ngoại tiếp bằng 2,5cm.
Đề bài
Tính diện tích của một hình chữ nhật, biết rằng hình chữ nhật đó có chiều dài gấp hai lần chiều rộng và bán kính đường tròn ngoại tiếp bằng 2,5cm.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+ Xét hình chữ nhật ABCD có \(AB = 2CB\) nội tiếp đường tròn (O).
+ Bán kính đường tròn ngoại tiếp 2,5cm nên đường chéo của hình chữ nhật bằng 5cm.
+ Áp dụng định lí Pythagore vào tam giác ABC vuông tại B tính được AB, BC.
+ Diện tích hình chữ nhật ABCD là: \(S = AB.BC\).
Lời giải chi tiết
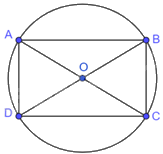
Xét hình chữ nhật ABCD có \(AB = 2CB\) nội tiếp đường tròn (O) bán kính 2,5cm.
Vì ABCD là hình chữ nhật nên ABCD nội tiếp đường tròn (O) có đường kính \(AC = 5cm\).
Áp dụng định lí Pythagore vào tam giác ABC vuông tại B ta có:
\(A{B^2} + B{C^2} = A{C^2}\)
\(4B{C^2} + B{C^2} = 25\)
\(BC = \sqrt 5 cm\) nên \(AB = 2\sqrt 5 cm\)
Vậy diện tích hình chữ nhật ABCD là:
\(S = AB.BC = 2\sqrt 5 .\sqrt 5 = 10\left( {c{m^2}} \right)\).
Bài tập 9.22 trang 83 SGK Toán 9 tập 2 yêu cầu học sinh giải một bài toán thực tế liên quan đến hàm số bậc hai. Để giải bài tập này, chúng ta cần nắm vững các kiến thức sau:
Trước khi bắt tay vào giải bài tập, chúng ta cần đọc kỹ đề bài và phân tích các thông tin đã cho. Xác định rõ yêu cầu của bài toán và tìm ra hướng giải phù hợp. Thông thường, các bài toán liên quan đến hàm số bậc hai sẽ yêu cầu chúng ta:
(Nội dung lời giải chi tiết bài tập 9.22 sẽ được trình bày tại đây. Bao gồm các bước giải, giải thích rõ ràng, và sử dụng các công thức toán học cần thiết. Ví dụ:)
Đề bài: Một quả bóng được ném lên từ mặt đất với vận tốc ban đầu là 15 m/s. Giả sử rằng quả bóng chuyển động theo một quỹ đạo parabol. Hãy viết phương trình mô tả quỹ đạo của quả bóng và tìm độ cao lớn nhất mà quả bóng đạt được.
Giải:
Chọn hệ tọa độ Oxy với gốc O tại vị trí ném bóng, trục Ox nằm ngang và trục Oy hướng lên trên. Gọi x là khoảng cách ngang từ vị trí ném bóng đến vị trí của quả bóng, và y là độ cao của quả bóng so với mặt đất.
Phương trình mô tả quỹ đạo của quả bóng có dạng: y = ax2 + bx + c
Vì quả bóng được ném lên từ mặt đất, nên khi x = 0 thì y = 0. Suy ra c = 0.
Vận tốc ban đầu của quả bóng là 15 m/s, nên hệ số a = -5 (do trọng lực). Vậy phương trình quỹ đạo của quả bóng là: y = -5x2 + 15x
Để tìm độ cao lớn nhất mà quả bóng đạt được, ta cần tìm tọa độ đỉnh của parabol. Hoành độ đỉnh của parabol là: x = -b / (2a) = -15 / (2 * -5) = 1.5
Độ cao lớn nhất mà quả bóng đạt được là: y = -5 * (1.5)2 + 15 * 1.5 = 11.25 (m)
Kết luận: Phương trình mô tả quỹ đạo của quả bóng là y = -5x2 + 15x và độ cao lớn nhất mà quả bóng đạt được là 11.25 mét.
Để củng cố kiến thức về hàm số bậc hai và ứng dụng trong giải quyết các bài toán thực tế, các em có thể luyện tập thêm các bài tập sau:
Bài tập 9.22 trang 83 SGK Toán 9 tập 2 - Kết nối tri thức là một bài tập điển hình về ứng dụng của hàm số bậc hai trong giải quyết các bài toán thực tế. Hy vọng rằng, với lời giải chi tiết và hướng dẫn cụ thể trong bài viết này, các em học sinh sẽ nắm vững kiến thức và tự tin làm bài tập.
Giaitoan.edu.vn luôn là địa chỉ tin cậy cho các em học sinh trong quá trình học tập môn Toán. Hãy truy cập website của chúng tôi để khám phá thêm nhiều tài liệu học tập hữu ích khác.