Bài tập 9.42 trang 92 SGK Toán 9 tập 2 thuộc chương trình Toán 9 Kết nối tri thức, yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế. Bài tập này thường gặp trong các kỳ thi và kiểm tra, do đó việc nắm vững phương pháp giải là vô cùng quan trọng.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 9.42 trang 92 SGK Toán 9 tập 2, giúp các em học sinh hiểu rõ bản chất của bài toán và tự tin giải các bài tập tương tự.
Cho một hình lục giác đều và một hình vuông cùng nội tiếp một đường tròn. Biết rằng hình vuông có cạnh bằng 3cm. Tính chu vi và diện tích của một hình lục giác đều đã cho.
Đề bài
Cho một hình lục giác đều và một hình vuông cùng nội tiếp một đường tròn. Biết rằng hình vuông có cạnh bằng 3cm. Tính chu vi và diện tích của một hình lục giác đều đã cho.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+ Gọi hình vuông ABCD và lục giác đều EFGHIJ cùng nội tiếp đường tròn (O).
+ Áp dụng định lí Pythagore vào tam giác ABC vuông tại B để tính AC, từ đó suy ra bán kính (O).
+ Chứng minh \(\Delta EOF = \Delta GOF = \Delta GOH = \Delta IOH = \Delta IOJ = \Delta EOJ\left( {c.c.c} \right)\), suy ra \(\widehat {EOF} = \widehat {FOG} = \widehat {GOH} = \widehat {HOI} = \widehat {IOJ} = \widehat {JOE} = \frac{{{{360}^o}}}{6} = {60^o}\)
+ Chứng minh tam giác EOF đều, từ đó tính được EF.
+ Chu vi lục giác đều EFGHIJ là: \(P = 6EF\).
+ Tính diện tích tam giác EOF.
+ Diện tích lục giác EFGHIJ bằng 6 lần diện tích tam giác EOF.
Lời giải chi tiết
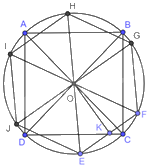
Gọi hình vuông ABCD và lục giác đều EFGHIJ cùng nội tiếp đường tròn (O).
Áp dụng định lí Pythagore vào tam giác ABC vuông tại B có:
\(A{C^2} = A{B^2} + B{C^2} \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = 3\sqrt 2 \left( {cm} \right)\)
Do đó, bán kính đường tròn (O) bằng \(\frac{{3\sqrt 2 }}{2}cm\).
Vì EFGHIJ là lục giác đều \(EF = FG = GH = HI = IJ = JE\)
Mà lục giác EFGHIJ nội tiếp (O) nên \(OE = OF = OG = OH = OI = OJ\).
Do đó, \(\Delta EOF = \Delta GOF = \Delta GOH = \Delta IOH = \Delta IOJ = \Delta EOJ\left( {c.c.c} \right)\)
Suy ra, \(\widehat {EOF} = \widehat {FOG} = \widehat {GOH} = \widehat {HOI} = \widehat {IOJ} = \widehat {JOE} = \frac{{{{360}^o}}}{6} = {60^o}\)
Tam giác EOF có: \(OE = OF,\widehat {EOF} = {60^o}\) nên tam giác EOF đều.
Do đó, \(OE = EF = \frac{{3\sqrt 2 }}{2}cm\)
Chu vi lục giác đều EFGHIJ là: \(P = 6EF = 6.\frac{{3\sqrt 2 }}{2} = 9\sqrt 2 \left( {cm} \right)\)
Kẻ OK vuông góc với EF tại K. Khi đó, OK là đường trung tuyến trong tam giác đều EOF.
Suy ra: \(EK = \frac{1}{2}EF = \frac{{3\sqrt 2 }}{4}cm\)
Áp dụng định lí Pythagore vào tam giác OKE vuông tại K có:
\(O{K^2} + K{E^2} = O{E^2} \Rightarrow OK = \sqrt {O{E^2} - K{E^2}} = \frac{{3\sqrt 6 }}{4}\left( {cm} \right)\)
Diện tích tam giác EOF là:
\({S_{EOF}} = \frac{1}{2}OK.EF = \frac{1}{2}.\frac{{3\sqrt 6 }}{4}.\frac{{3\sqrt 2 }}{2} = \frac{{9\sqrt 3 }}{8}\left( {c{m^2}} \right)\)
Vì \(\Delta EOF = \Delta GOF = \Delta GOH = \Delta IOH = \Delta IOJ = \Delta EOJ\) nên
\({S_{EFGHIJ}} = 6{S_{\Delta EOF}} = 6.\frac{{9\sqrt 3 }}{8} = \frac{{27\sqrt 3 }}{4}\left( {c{m^2}} \right)\)
Bài tập 9.42 trang 92 SGK Toán 9 tập 2 yêu cầu học sinh giải một bài toán thực tế liên quan đến hàm số bậc hai. Để giải bài tập này, chúng ta cần nắm vững các kiến thức sau:
Trước khi bắt tay vào giải bài tập, chúng ta cần đọc kỹ đề bài và phân tích các thông tin đã cho. Xác định rõ các yếu tố liên quan đến hàm số bậc hai, chẳng hạn như các điểm mà đồ thị hàm số đi qua, các điều kiện ràng buộc, hoặc các yêu cầu cụ thể của bài toán.
Sau khi phân tích đề bài, chúng ta cần tìm ra hướng giải phù hợp. Thông thường, để giải các bài toán liên quan đến hàm số bậc hai, chúng ta có thể sử dụng các phương pháp sau:
(Nội dung lời giải chi tiết bài tập 9.42 sẽ được trình bày tại đây, bao gồm các bước giải, các phép tính, và các giải thích rõ ràng. Lời giải cần được trình bày một cách logic và dễ hiểu, giúp học sinh nắm vững phương pháp giải bài tập.)
Để giúp các em học sinh hiểu rõ hơn về phương pháp giải bài tập 9.42, chúng ta sẽ cùng xem xét một số ví dụ minh họa. Sau đó, chúng ta sẽ đưa ra một số bài tập tương tự để các em tự luyện tập và củng cố kiến thức.
Khi giải các bài tập về hàm số bậc hai, các em cần lưu ý những điều sau:
Bài tập 9.42 trang 92 SGK Toán 9 tập 2 là một bài tập quan trọng giúp các em học sinh củng cố kiến thức về hàm số bậc hai và rèn luyện kỹ năng giải quyết các bài toán thực tế. Hy vọng rằng, với lời giải chi tiết và các hướng dẫn cụ thể mà Giaitoan.edu.vn đã cung cấp, các em sẽ tự tin giải quyết bài tập này và đạt kết quả tốt trong các kỳ thi sắp tới.
| Công thức | Mô tả |
|---|---|
| y = ax2 + bx + c | Dạng tổng quát của hàm số bậc hai |
| x = -b / 2a | Hoành độ đỉnh của parabol |
| Δ = b2 - 4ac | Biệt thức của phương trình bậc hai |