Bài tập 4.19 trang 80 SGK Toán 9 tập 1 thuộc chương Hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế. Giaitoan.edu.vn sẽ cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác, cập nhật và hữu ích nhất cho học sinh. Hãy cùng giaitoan.edu.vn khám phá lời giải bài tập 4.19 này nhé!
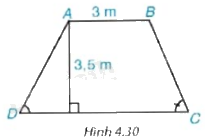
Mặt cắt ngang của một đập ngăn nước có dạng hình thang ABCD (H.4.30) . Chiều rộng của mặt trên AB của đập là 3 m. Độ dốc của sườn AD, tức là (tan D = 1,25.) Độ dốc của sườn BC, tức là (tan C = 1,5.) Chiều cao của đập là 3,5 m. Hãy tính chiều rộng CD của chân đập, chiều dài của các sườn AD và BC (làm tròn đến dm) .
Đề bài
Mặt cắt ngang của một đập ngăn nước có dạng hình thang ABCD (H.4.30) . Chiều rộng của mặt trên AB của đập là 3 m. Độ dốc của sườn AD, tức là \(\tan D = 1,25.\) Độ dốc của sườn BC, tức là \(\tan C = 1,5.\) Chiều cao của đập là 3,5 m. Hãy tính chiều rộng CD của chân đập, chiều dài của các sườn AD và BC (làm tròn đến dm).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Gọi H là chân đường vuông góc kẻ từ A, ta mới tính được cạnh AD và DH dựa theo tỉ số lượng giác, chưa đủ để tính cạnh DC và BC, do đó ta kẻ thêm đường cao BK của hình thang, ta sẽ có ABKH là hình chữ nhật, ta tính được cạnh HK, tam giác BCK tính được BC và CK. Để tính DC ta tổng độ dài 3 cạnh DH, HK, KC. Chú ý làm tròn đến đơn vị dm tức là phần thập phân lấy 1 chữ số.
Lời giải chi tiết
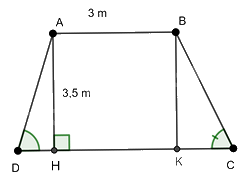
Kẻ BK vuông góc với DC tại K và AH vuông góc với DC tại H nên hình thang có hai đường cao là AH và BK; AB= BK = 3,5 m
Xét tứ giác ABKH có AH // BK; AH = BK; \(\widehat {AHK} = {90^0}\)
Nên ABKH là hình chữ nhật suy ra HK = AB = 3 m
Tam giác ADH vuông tại H nên ta có:
\(\tan \widehat D = \frac{{AH}}{{DH}}\) hay \(1,25 = \frac{{3,5}}{{DH}}\) suy ra \(DH = \frac{{3,5}}{{1,25}} = 2,8\) m = 28 dm.
\(A{D^2} = D{H^2} + A{H^2} = 3,{5^2} + 2,{8^2} = 20,09\) hay \(AD = \sqrt {20,09} \approx 4,5\) m = 45 dm (vì \(AD > 0\))
Tam giác BKC vuông tại K nên ta có:
\(\tan \widehat C = \frac{{BK}}{{KC}}\) hay \(1,5 = \frac{{3,5}}{{KC}}\) suy ra \(KC = \frac{{3,5}}{{1,5}} = \frac{7}{3} \approx 2,3\) m = 23 dm.
\(B{C^2} = B{K^2} + K{C^2} = 3,{5^2} + 2,{3^2} = 17,54\) hay \(BC = \sqrt {17,54} \approx 4,2\) m =42 dm (vì \(BC > 0\))
Độ dài cạnh DC là \(DC = DH + HK + KC \approx 2,8 + 3 + 2,3 = 8,1m \approx 81dm\)
Bài tập 4.19 trang 80 SGK Toán 9 tập 1 - Kết nối tri thức là một bài toán ứng dụng thực tế về hàm số bậc nhất. Để giải bài tập này, học sinh cần nắm vững các kiến thức sau:
Nội dung bài tập 4.19:
Một người đi xe đạp từ A đến B với vận tốc 12km/h. Hỏi người đó đi hết bao lâu nếu quãng đường AB dài 36km?
Lời giải:
Gọi t (giờ) là thời gian người đó đi từ A đến B.
Quãng đường AB là 36km, vận tốc của người đi xe đạp là 12km/h. Ta có công thức:
Quãng đường = Vận tốc × Thời gian
=> 36 = 12 × t
=> t = 36 / 12
=> t = 3
Vậy người đó đi hết 3 giờ để đi từ A đến B.
Bài tập 4.19 là một ví dụ điển hình về ứng dụng hàm số bậc nhất vào việc giải quyết các bài toán thực tế liên quan đến chuyển động. Trong bài toán này, quãng đường là hàm số bậc nhất của thời gian, với vận tốc đóng vai trò là hệ số góc.
Để hiểu sâu hơn về ứng dụng của hàm số bậc nhất, học sinh có thể thực hành giải các bài tập tương tự với các thông số khác nhau. Ví dụ:
Ngoài ra, học sinh cũng có thể tìm hiểu về các ứng dụng khác của hàm số bậc nhất trong các lĩnh vực như kinh tế, vật lý, và kỹ thuật.
Ngoài bài tập 4.19, còn rất nhiều dạng bài tập tương tự liên quan đến hàm số bậc nhất. Dưới đây là một số dạng bài tập phổ biến và phương pháp giải:
Để giải quyết các dạng bài tập này, học sinh cần nắm vững các kiến thức cơ bản về hàm số bậc nhất và luyện tập thường xuyên. Giaitoan.edu.vn sẽ cung cấp thêm nhiều bài tập và lời giải chi tiết để giúp các em học sinh ôn tập và củng cố kiến thức.
Bài tập 4.19 trang 80 SGK Toán 9 tập 1 - Kết nối tri thức là một bài toán ứng dụng thực tế về hàm số bậc nhất. Việc giải bài tập này giúp học sinh hiểu rõ hơn về ứng dụng của hàm số bậc nhất trong cuộc sống và rèn luyện kỹ năng giải quyết các bài toán thực tế. Hy vọng với lời giải chi tiết và phân tích sâu sắc của giaitoan.edu.vn, các em học sinh sẽ tự tin hơn trong việc học tập môn Toán.