Chào mừng bạn đến với bài học về lý thuyết khai căn bậc hai và các phép toán liên quan trong chương trình Toán 9 Kết nối tri thức. Bài học này sẽ cung cấp cho bạn những kiến thức nền tảng quan trọng, giúp bạn giải quyết các bài toán một cách hiệu quả.
Chúng ta sẽ cùng nhau tìm hiểu về điều kiện xác định của căn bậc hai, các quy tắc khai căn, và cách áp dụng chúng vào các phép nhân, chia căn bậc hai.
1. Khai căn bậc hai và phép nhân Liên hệ giữa phép khai căn bậc hai và phép nhân
1. Khai căn bậc hai và phép nhân
Liên hệ giữa phép khai căn bậc hai và phép nhân
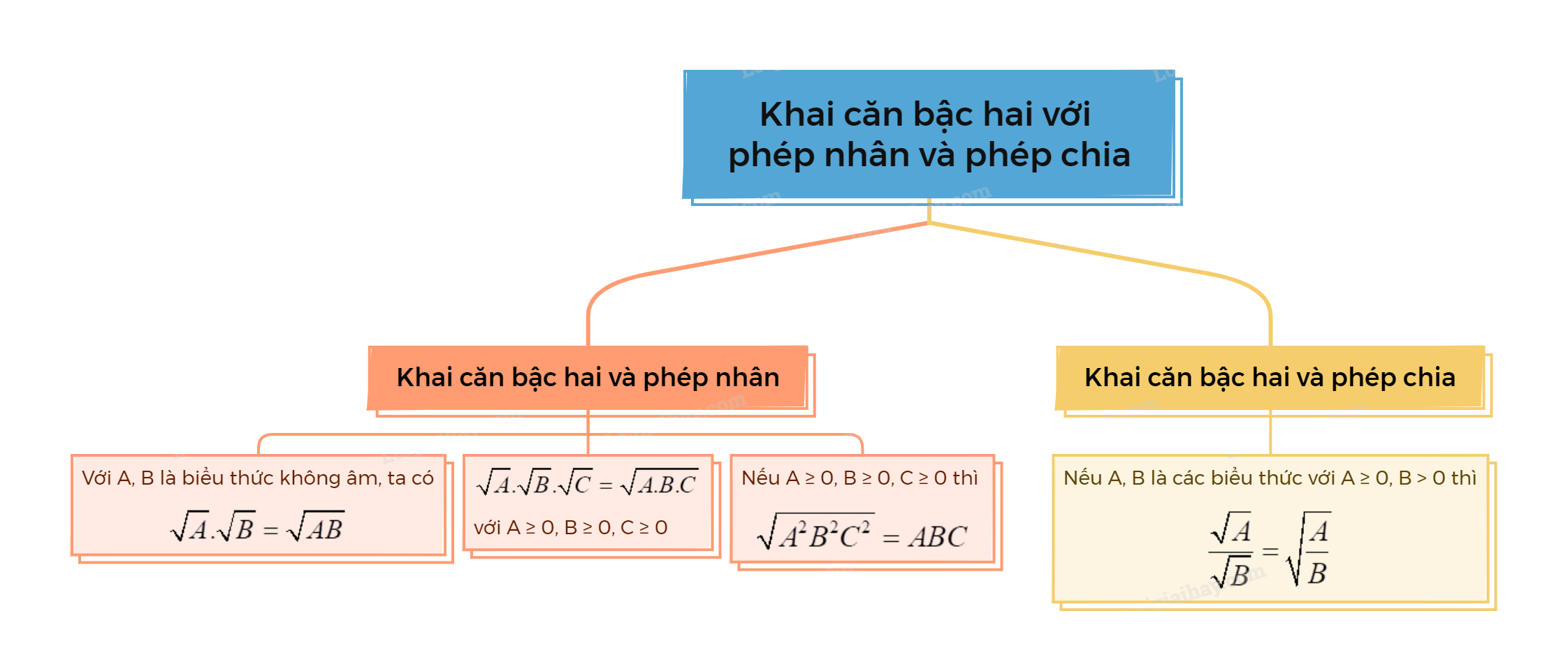
Với A, B là biểu thức không âm, ta có \(\sqrt A .\sqrt B = \sqrt {AB} \). |
Ví dụ:
\(\sqrt {27} .\sqrt 3 = \sqrt {27.3} = \sqrt {81} = 9\)
\(\sqrt 5 \left( {\sqrt {125} + \sqrt 5 } \right) = \sqrt 5 .\sqrt {125} + \sqrt 5 .\sqrt 5 = \sqrt {5.125} + \sqrt {5.5} = 25 + 5 = 30\)
Chú ý:
- Kết quả trên có thể mở rộng cho nhiều biểu thức không âm, chẳng hạn:
\(\sqrt A .\sqrt B .\sqrt C = \sqrt {A.B.C} \) (với \(A \ge 0,B \ge 0,C \ge 0\)).
Ví dụ: \(\sqrt 3 .\sqrt 5 .\sqrt {15} = \sqrt {3.5.15} = \sqrt {225} = 15\)
- Nếu \(A \ge 0,B \ge 0,C \ge 0\) thì \(\sqrt {{A^2}{B^2}{C^2}} = ABC\).
Ví dụ: Với \(a \ge 0,b < 0\) thì \(\sqrt {25{a^2}{b^2}} = \sqrt {{5^2}.{a^2}.{{\left( { - b} \right)}^2}} = \sqrt {{5^2}} .\sqrt {{a^2}} .\sqrt {{{\left( { - b} \right)}^2}} = 5.a.\left( { - b} \right) = - 5ab\)
2. Khai căn bậc hai và phép chia
Liên hệ giữa phép khai căn bậc hai và phép chia
Nếu A, B là các biểu thức với \(A \ge 0,B > 0\) thì \(\frac{{\sqrt A }}{{\sqrt B }} = \sqrt {\frac{A}{B}} \). |
Ví dụ: \(\frac{{\sqrt 8 }}{{\sqrt 2 }} = \sqrt {\frac{8}{2}} = \sqrt 4 = 2\);
Với \(a > 0\) thì \(\frac{{\sqrt {52{a^3}} }}{{\sqrt {13a} }} = \sqrt {\frac{{52{a^3}}}{{13a}}} = \sqrt {4{a^2}} = \sqrt {{{\left( {2a} \right)}^2}} = 2a\).
Khai căn bậc hai là một trong những khái niệm quan trọng trong chương trình Toán 9, đặc biệt là chương trình Kết nối tri thức. Việc nắm vững lý thuyết và các quy tắc liên quan sẽ giúp học sinh giải quyết các bài toán một cách nhanh chóng và chính xác.
Căn bậc hai của một số thực a (với a ≥ 0) là số x sao cho x2 = a. Ký hiệu: √a. Ví dụ, √9 = 3 vì 32 = 9.
Căn bậc hai của một số thực chỉ xác định khi số đó lớn hơn hoặc bằng 0. Tức là, √a chỉ có nghĩa khi a ≥ 0.
Để nhân hai căn bậc hai, ta áp dụng quy tắc: √a * √b = √(a * b) (với a ≥ 0, b ≥ 0). Ví dụ: √2 * √8 = √(2 * 8) = √16 = 4.
Để chia hai căn bậc hai, ta áp dụng quy tắc: √a / √b = √(a / b) (với a ≥ 0, b > 0). Ví dụ: √18 / √2 = √(18 / 2) = √9 = 3.
Để đơn giản hóa các biểu thức chứa căn bậc hai, ta thường sử dụng các quy tắc khai căn, quy tắc nhân và chia căn bậc hai, và các phép biến đổi đại số khác.
Ví dụ 1: Rút gọn biểu thức √(27 * 5). Ta có: √(27 * 5) = √27 * √5 = √(9 * 3) * √5 = 3√3 * √5 = 3√(3 * 5) = 3√15.
Ví dụ 2: Rút gọn biểu thức (√12 + √3) / √3. Ta có: (√12 + √3) / √3 = √12 / √3 + √3 / √3 = √(12 / 3) + 1 = √4 + 1 = 2 + 1 = 3.
Việc luyện tập thường xuyên với các bài tập khác nhau sẽ giúp bạn nắm vững lý thuyết và các quy tắc khai căn bậc hai, từ đó giải quyết các bài toán một cách tự tin và hiệu quả. Hãy nhớ luôn kiểm tra điều kiện xác định của căn bậc hai trước khi thực hiện bất kỳ phép toán nào.
Hy vọng bài học này đã cung cấp cho bạn những kiến thức hữu ích về lý thuyết khai căn bậc hai và các phép nhân, chia căn bậc hai trong chương trình Toán 9 Kết nối tri thức. Chúc bạn học tập tốt!