Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9. Bài viết này sẽ hướng dẫn bạn giải bài tập 5 trang 127 SGK Toán 9 tập 2 - Kết nối tri thức một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức. Vì vậy, chúng tôi luôn cố gắng trình bày lời giải một cách rõ ràng, logic và dễ tiếp thu nhất.
Kí hiệu (left( {{d_1}} right)) là đường thẳng (x + 2y = 4,left( {{d_2}} right)) là đường thẳng (x - y = 1). a) Vẽ (left( {{d_1}} right)) và (left( {{d_2}} right)) trên cùng một mặt phẳng tọa độ. b) Giải hệ phương trình (left{ begin{array}{l}x + 2y = 4\x - y = 1end{array} right.) để tìm tọa độ giao điểm của hai đường thẳng (left( {{d_1}} right)) và (left( {{d_2}} right)).
Đề bài
Kí hiệu \(\left( {{d_1}} \right)\) là đường thẳng \(x + 2y = 4,\left( {{d_2}} \right)\) là đường thẳng \(x - y = 1\).
a) Vẽ \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) trên cùng một mặt phẳng tọa độ.
b) Giải hệ phương trình \(\left\{ \begin{array}{l}x + 2y = 4\\x - y = 1\end{array} \right.\) để tìm tọa độ giao điểm của hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Đường thẳng \(\left( {{d_1}} \right)\) đi qua hai điểm \(A\left( {0;2} \right),B\left( {4;0} \right)\).
Đường thẳng \(\left( {{d_2}} \right)\) đi qua hai điểm \(C\left( {0; - 1} \right),D\left( {1;0} \right)\).
Biểu diễn các điểm A, B, C, D trên cùng một mặt phẳng tọa độ Oxy.
b) Giải hệ phương trình bằng phương pháp cộng đại số: Để giải một hệ hai phương trình bậc nhất hai ẩn có hệ số của cùng một ẩn nào đó trong hai phương trình bằng nhau hoặc đối nhau, ta có thể làm như sau:
Bước 1. Cộng hay trừ từng vế của hai phương trình trong hệ được phương trình chỉ còn chứa một ẩn.
Bước 2. Giải phương trình một ẩn vừa nhận được, từ đó suy ra nghiệm của hệ phương trình đã cho.
+ Trường hợp hệ phương trình đã cho không có hai hệ số của cùng một ẩn bằng nhau hoặc đối nhau, ta có thể đưa về trường hợp đã xét bằng cách nhân hai vế của mỗi phương trình với một số thích hợp (khác 0).
Lời giải chi tiết
a) Đường thẳng \(\left( {{d_1}} \right)\) đi qua hai điểm \(A\left( {0;2} \right),B\left( {4;0} \right)\).
Đường thẳng \(\left( {{d_2}} \right)\) đi qua hai điểm \(C\left( {0; - 1} \right),D\left( {1;0} \right)\).
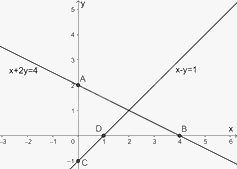
b) Trừ từng vế hai phương trình ta được \(\left( {x + 2y} \right) - \left( {x - y} \right) = 4 - 1\), hay \(3y = 3\), suy ra \(y = 1\).
Thế \(y = 1\) vào phương trình thứ hai của hệ đã cho ta có: \(x - 1 = 1\) nên \(x = 2\).
Do đó, tọa độ giao điểm của hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) là (2; 1).
Bài tập 5 trang 127 SGK Toán 9 tập 2 - Kết nối tri thức thuộc chương trình học Toán 9, tập trung vào việc vận dụng kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như:
Trước khi bắt đầu giải bài tập, học sinh cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Điều này giúp học sinh tập trung vào việc tìm kiếm lời giải phù hợp và tránh những sai sót không đáng có.
Thông thường, bài tập 5 trang 127 SGK Toán 9 tập 2 - Kết nối tri thức yêu cầu học sinh:
Để giúp học sinh hiểu rõ hơn về cách giải bài tập này, chúng tôi sẽ trình bày lời giải chi tiết cho từng phần của bài tập. Lưu ý rằng, lời giải này chỉ mang tính chất tham khảo, học sinh cần tự mình suy nghĩ và vận dụng kiến thức để giải bài tập một cách độc lập.
Để xác định hàm số bậc hai, học sinh cần tìm các hệ số a, b, c trong biểu thức y = ax2 + bx + c. Các hệ số này có thể được xác định từ các thông tin cho trước trong đề bài, chẳng hạn như:
Sau khi xác định được hàm số bậc hai, học sinh cần vẽ đồ thị của hàm số. Để vẽ đồ thị, học sinh có thể thực hiện các bước sau:
Tọa độ đỉnh của đồ thị hàm số y = ax2 + bx + c được tính theo công thức:
xđỉnh = -b / 2a
yđỉnh = -Δ / 4a (với Δ = b2 - 4ac)
Trục đối xứng của đồ thị hàm số là đường thẳng x = xđỉnh.
Giao điểm của đồ thị hàm số với trục Oy là điểm có tọa độ (0, c).
Giao điểm của đồ thị hàm số với trục Ox là nghiệm của phương trình ax2 + bx + c = 0.
Trong các bài toán ứng dụng, hàm số bậc hai thường được sử dụng để mô tả các hiện tượng thực tế, chẳng hạn như:
Để giải các bài toán này, học sinh cần vận dụng kiến thức về hàm số bậc hai để xây dựng phương trình toán học mô tả hiện tượng thực tế và giải phương trình đó để tìm ra kết quả.
Để nắm vững kiến thức về hàm số bậc hai và rèn luyện kỹ năng giải bài tập, học sinh nên thực hành giải nhiều bài tập khác nhau. Ngoài ra, học sinh có thể tham khảo các tài liệu học tập khác, chẳng hạn như sách giáo khoa, sách bài tập, các trang web học toán online, hoặc tìm kiếm sự giúp đỡ từ giáo viên và bạn bè.
Bài tập 5 trang 127 SGK Toán 9 tập 2 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc hai và rèn luyện kỹ năng giải bài tập. Hy vọng rằng, với hướng dẫn chi tiết này, học sinh sẽ có thể giải bài tập này một cách dễ dàng và hiệu quả.