Bài tập 9.12 trang 76 SGK Toán 9 tập 2 thuộc chương trình Toán 9 Kết nối tri thức, yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế. Bài tập này thường gặp trong các kỳ thi và kiểm tra, do đó việc nắm vững phương pháp giải là vô cùng quan trọng.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 9.12 trang 76 SGK Toán 9 tập 2, giúp các em học sinh hiểu rõ bản chất của bài toán và tự tin giải các bài tập tương tự.
Người ta muốn làm một khung gỗ tam giác đều để đặt vừa khít một chiếc đồng hồ hình tròn có đường kính 30cm (H.9.23). Hỏi độ dài các cạnh (phía bên trong) của khung gỗ phải bằng bao nhiêu?
Đề bài
Người ta muốn làm một khung gỗ tam giác đều để đặt vừa khít một chiếc đồng hồ hình tròn có đường kính 30cm (H.9.23). Hỏi độ dài các cạnh (phía bên trong) của khung gỗ phải bằng bao nhiêu?

Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+ Gọi khung gỗ hình tam giác đều là tam giác ABC. Đồng hồ là đường tròn tâm I, có đường kính 30cm
+ Gọi H là giao điểm của AI và BC nên IH là bán kính đường tròn nội tiếp tam giác ABC.
+ Ta có: \(IH = \frac{{\sqrt 3 }}{6}BC\), từ đó tính được BC.
Lời giải chi tiết
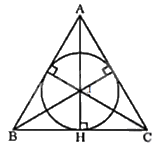
Gọi khung gỗ hình tam giác đều là tam giác ABC.
Đồng hồ là đường tròn tâm I, bán kính \(IH = \frac{{30}}{2} = 15cm\)
Vì (I; IH) nội tiếp tam giác đều ABC nên \(IH = \frac{{\sqrt 3 }}{6}BC\), \(15 = \frac{{\sqrt 3 }}{6}BC\) nên \(BC = 30\sqrt 3 \left( {cm} \right)\)
Vậy độ dài cạnh khung gỗ phía bên trong bằng \(30\sqrt 3 cm\).
Bài tập 9.12 SGK Toán 9 tập 2 Kết nối tri thức là một bài toán ứng dụng thực tế về hàm số bậc hai. Để giải bài toán này, học sinh cần nắm vững các kiến thức sau:
Đề bài: (Nội dung đề bài đầy đủ của bài tập 9.12)
Lời giải:
Dựa vào thông tin đề bài, ta xác định được hàm số bậc hai có dạng y = ax2 + bx + c. Xác định các hệ số a, b, c dựa trên các điểm cho trước hoặc các thông tin khác trong đề bài.
Để tìm hoành độ giao điểm của đồ thị hàm số với trục hoành, ta giải phương trình ax2 + bx + c = 0. Sử dụng công thức nghiệm của phương trình bậc hai để tìm ra các giá trị của x.
Dựa vào các giá trị x tìm được, ta có thể kết luận về vị trí giao điểm của đồ thị hàm số với trục hoành. Ngoài ra, cần kiểm tra lại kết quả để đảm bảo tính chính xác.
Giả sử đề bài cho hàm số y = x2 - 4x + 3. Để tìm hoành độ giao điểm của đồ thị hàm số với trục hoành, ta giải phương trình:
x2 - 4x + 3 = 0
Sử dụng công thức nghiệm, ta có:
Δ = (-4)2 - 4 * 1 * 3 = 16 - 12 = 4
x1 = (4 + √4) / 2 = 3
x2 = (4 - √4) / 2 = 1
Vậy, đồ thị hàm số y = x2 - 4x + 3 cắt trục hoành tại hai điểm có hoành độ x = 1 và x = 3.
Để củng cố kiến thức, các em có thể tham khảo thêm các bài tập tương tự sau:
Giaitoan.edu.vn hy vọng với lời giải chi tiết và hướng dẫn cụ thể này, các em học sinh sẽ tự tin hơn khi giải bài tập 9.12 trang 76 SGK Toán 9 tập 2 - Kết nối tri thức và đạt kết quả tốt trong môn Toán.
Chúc các em học tập tốt!