Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng về vị trí tương đối giữa đường thẳng và đường tròn trong chương trình Toán 9 Kết nối tri thức. Chúng ta sẽ cùng nhau khám phá các trường hợp có thể xảy ra và cách xác định chúng.
Nắm vững lý thuyết này là nền tảng để giải quyết các bài toán liên quan đến đường thẳng và đường tròn, đồng thời giúp bạn hiểu sâu hơn về hình học phẳng.
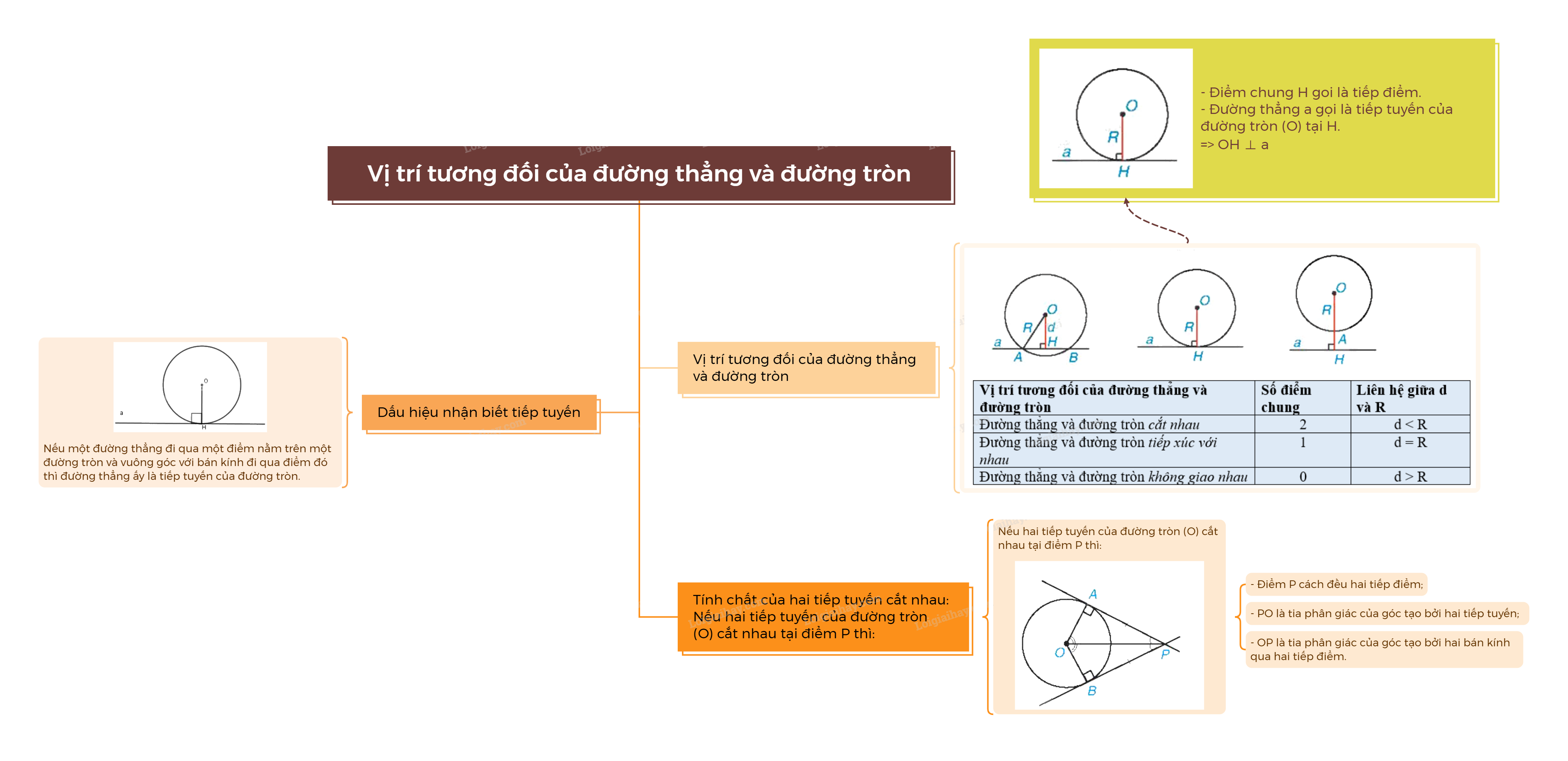
1. Vị trí tương đối của đường thẳng và đường tròn
1. Vị trí tương đối của đường thẳng và đường tròn
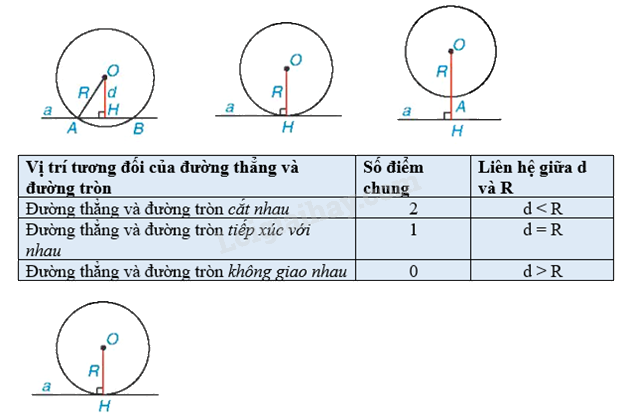
Điểm chung H của đường thẳng và đường tròn tiếp xúc với nhau goi là tiếp điểm. Khi đó đường thẳng a còn gọi là tiếp tuyếncủa đường tròn (O) tại H.
Đường thẳng a tiếp xúc với đường tròn (O) tại H thì \(OH \bot a\).
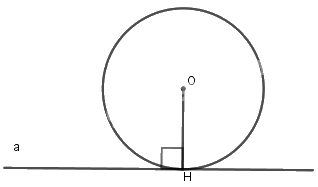
2. Dấu hiệu nhận biết tiếp tuyến của đường tròn
Dấu hiệu nhận biết tiếp tuyến
Nếu một đường thẳng đi qua một điểm nằm trên một đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là tiếp tuyến của đường tròn. |
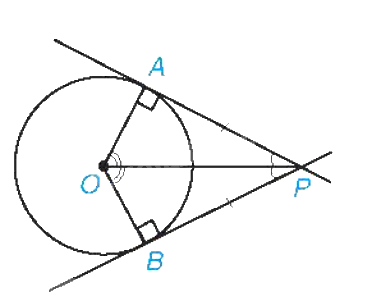
3. Hai tiếp tuyến cắt nhau của một đường tròn
Tính chất của hai tiếp tuyến cắt nhau
Nếu hai tiếp tuyến của đường tròn (O) cắt nhau tại điểm P thì: - Điểm P cách đều hai tiếp điểm; - PO là tia phân giác của góc tạo bởi hai tiếp tuyến; - OP là tia phân giác của góc tạo bởi hai bán kính qua hai tiếp điểm. |
Ví dụ: Cho đường tròn (O), B, C \( \in \) (O). Tiếp tuyến của (O) tại B và C cắt nhau tại A.
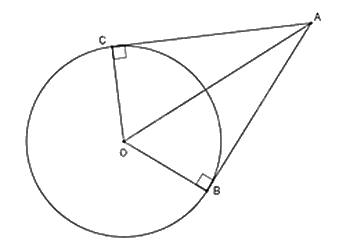
Khi đó:
- AB = AC
- Tia AO là tia phân giác của \(\widehat {BAC}\).
- Tia OA là tia phân giác của \(\widehat {BOC}\).
Trong hình học phẳng, việc xác định vị trí tương đối giữa đường thẳng và đường tròn là một vấn đề cơ bản và quan trọng. Nó là nền tảng để giải quyết nhiều bài toán liên quan đến đường tròn và đường thẳng, cũng như các ứng dụng thực tế.
Đường thẳng và đường tròn có thể có ba vị trí tương đối với nhau:
Đường thẳng d không giao nhau với đường tròn (O; R) khi và chỉ khi khoảng cách từ tâm O đến đường thẳng d lớn hơn bán kính R.
Ký hiệu: d(O, d) > R
Đường thẳng d tiếp xúc với đường tròn (O; R) khi và chỉ khi khoảng cách từ tâm O đến đường thẳng d bằng bán kính R.
Ký hiệu: d(O, d) = R
Có hai loại tiếp xúc:
Đường thẳng d giao nhau với đường tròn (O; R) tại hai điểm khi và chỉ khi khoảng cách từ tâm O đến đường thẳng d nhỏ hơn bán kính R.
Ký hiệu: d(O, d) < R
Để xác định vị trí tương đối của đường thẳng và đường tròn, ta thực hiện các bước sau:
Ví dụ 1: Cho đường tròn (O; 5cm) và đường thẳng d có khoảng cách đến tâm O là 3cm. Xác định vị trí tương đối của đường thẳng d và đường tròn (O; 5cm).
Giải: Vì d(O, d) = 3cm < 5cm = R, nên đường thẳng d giao nhau với đường tròn (O; 5cm) tại hai điểm.
Ví dụ 2: Cho đường tròn (O; 4cm) và đường thẳng d có khoảng cách đến tâm O là 4cm. Xác định vị trí tương đối của đường thẳng d và đường tròn (O; 4cm).
Giải: Vì d(O, d) = 4cm = 4cm = R, nên đường thẳng d tiếp xúc với đường tròn (O; 4cm).
1. Cho đường tròn (O; 6cm) và đường thẳng d có khoảng cách đến tâm O là 7cm. Xác định vị trí tương đối của đường thẳng d và đường tròn (O; 6cm).
2. Cho đường tròn (O; 2cm) và đường thẳng d có khoảng cách đến tâm O là 1cm. Xác định vị trí tương đối của đường thẳng d và đường tròn (O; 2cm).
Việc nắm vững lý thuyết về vị trí tương đối của đường thẳng và đường tròn là rất quan trọng trong quá trình học tập môn Toán. Hy vọng bài học này đã cung cấp cho bạn những kiến thức cần thiết và giúp bạn tự tin hơn khi giải các bài toán liên quan.