Giaitoan.edu.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 1 trang 6, 7, 8 sách giáo khoa Toán 9 tập 1 chương trình Kết nối tri thức. Bài viết này sẽ giúp học sinh nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi cung cấp đáp án đầy đủ, kèm theo các bước giải chi tiết, giúp các em học sinh có thể tự học tại nhà hoặc ôn tập kiến thức một cách hiệu quả.
Câu “Quýt, cam mười bảy quả tươi” có nghĩa là tổng số cam và số quýt là 17. Hãy viết hệ thức với hai biến x và y biểu thị giả thiết này.
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 1 trang 6 SGK Toán 9 Kết nối tri thức
Hãy viết một phương trình bậc nhất hai ẩn và chỉ ra một nghiệm của nó.
Phương pháp giải:
Phương trình bậc nhất hai ẩn x và y là hệ thức dạng \(ax + by = c\left( 1 \right)\) trong đó a,b và c là các số đã biết \(a \ne 0\) hoặc \(b \ne 0.\) Nên ta có thể chọn a, b,c là số thực bất kì.
Nếu thay \(x = {x_0};y = {y_0}\) vào phương trình số \(\left( 1 \right)\) thì ta có \(a{x_0} + b{y_0} = c\) là một khẳng định đúng thì \(\left( {{x_0};{y_0}} \right)\) là nghiệm của phương trình \(\left( 1 \right)\)
Lời giải chi tiết:
Ta có \(2x - y = 5\) là một phương trình bậc nhất hai ẩn.
Cặp số \(\left( {3;1} \right)\) là một nghiệm của phương trình \(2x - y = 5\) vì \(2.3 - 1 = 5.\) (luôn đúng).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 1 trang 6 SGK Toán 9 Kết nối tri thức
Câu “Quýt, cam mười bảy quả tươi” có nghĩa là tổng số cam và số quýt là 17. Hãy viết hệ thức với hai biến x và y biểu thị giả thiết này.
Phương pháp giải:
Phía trên của câu hỏi đã cho: Gọi x là số cam, y là số quýt ( với x, y nguyên dương)
Tổng số cam và số quýt tức là phép tính cộng x quả quýt và y quả cam
Lời giải chi tiết:
Hệ thức biểu thị: \(x + y = 17.\)
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 6 SGK Toán 9 Kết nối tri thức
Tương tự, hãy viết hệ thức với hai biến x và y biểu thị giả thiết cho bởi các câu thơ thứ ba, thứ tư và thứ năm.
Quýt, cam mười bảy quả tươi
Đem chia cho một trăm người cùng vui.
Chia ba mỗi quả quýt rồi,
Còn cam, mỗi quả chia mười vừa xinh.
Trăm người, trăm miếng ngọt lành.
Quýt, cam mỗi loại tính rành là bao?

Phương pháp giải:
- Câu thơ thứ 3 (Chia ba mỗi quả quýt rồi) tức là mỗi quả quýt thì ta sẽ có 3 miếng nên y quả sẽ có \(3y\) miếng
- Câu thơ thứ tư (Còn cam, mỗi quả chia mười vừa xinh) tức là mỗi quả cam thì ta sẽ có 10 miếng nên x quả sẽ có \(10x\) miếng
- Trăm người trăm miếng tức là số miếng quýt (\(3y\) miếng) và số miếng cam (\(10x\) miếng) tổng là 100 miếng
Lời giải chi tiết:
Hệ thức liên hệ giữa x và y qua các câu thơ thứ ba, thứ tư và thứ năm là \(10x + 3y = 100.\)
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 2 trang 8 SGK Toán 9 Kết nối tri thức
Viết nghiệm và biểu diễn hình học tất cả các nghiệm của mỗi phương trình bậc nhất hai ẩn sau:
a) \(2x - 3y = 5;\)
b) \(0x + y = 3;\)
c) \(x + 0y = - 2.\)
Phương pháp giải:
Để viết nghiệm của một phương trình bậc nhất hai ẩn, ta cần rút y theo x \(\left( {by = c - ax} \right)\) từ đó ta giải được \(y = \frac{{c - ax}}{b}\) với \(b \ne 0.\) Đối với trường hợp \(b = 0\) thì ta làm ngược lại (rút x theo y).
Biểu diễn hình học tất cả các nghiệm của phương trình bậc nhất hai ẩn là đường thẳng \(ax + by = c.\)
Lời giải chi tiết:
a) \(2x - 3y = 5;\)
Ta có \(y = \frac{{2x - 5}}{3}\) nên mỗi cặp số \(\left( x;\frac{{2x - 5}}{3} \right)\) với \(x \in \mathbb{R}\) tùy ý là một nghiệm của phương trình \(2x - 3y = 5.\)
Biểu diễn hình học tất cả các nghiệm của phương trình \(2x - 3y = 5.\)
Cho \(x = 0 \Rightarrow y = \frac{{ - 5}}{3} \Rightarrow A\left( {0;\frac{{ - 5}}{3}} \right)\)
\(y = 0 \Rightarrow x = \frac{5}{2} \Rightarrow B\left( {\frac{5}{2};0} \right)\)
Đường thẳng \(2x - 3y = 5\) đi qua hai điểm A và B
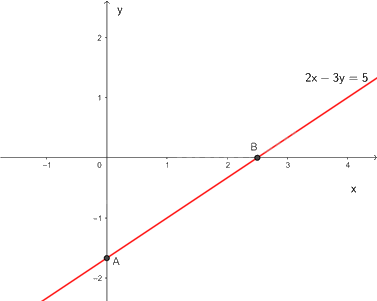
Các nghiệm là tọa độ của một điểm thuộc đường thẳng \(2x - 3y = 5.\)
b) \(0x + y = 3;\)
Ta có \(0x + y = 3\) rút gọn thành \(y = 3\) nên phương trình có nghiệm là \(\left( {x;3} \right)\) với \(x \in \mathbb{R}\) tùy ý.
Mỗi nghiệm này là tọa độ của một điểm thuộc đường thẳng song song với trục hoành và cắt trục tung tại điểm (0;3). Ta gọi đó là đường thẳng y = 3
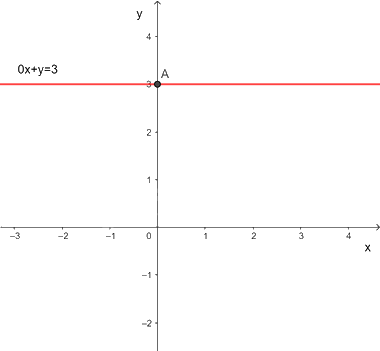
Các nghiệm là tọa độ của một điểm thuộc đường thẳng \(0x + y = 3.\)
c) \(x + 0y = - 2.\)
Ta có \(x + 0y = - 2\) rút gọn thành \(x = - 2\) nên phương trình có nghiệm là \(\left( { - 2;y} \right)\) với \(y \in \mathbb{R}\) tùy ý.
Mỗi nghiệm này là tọa độ của một điểm thuộc đường thẳng song song với trục tung và cắt trục hoành tại điểm (-2; 0). Ta gọi đó là đường thẳng x = -2
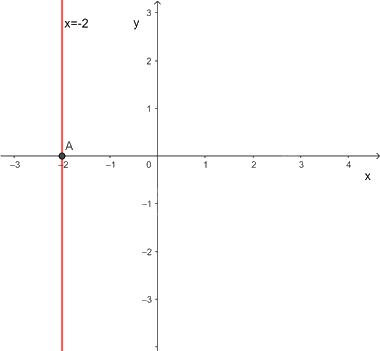
Các nghiệm là tọa độ của một điểm thuộc đường thẳng \(x + 0y = - 2.\)
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 1 trang 6 SGK Toán 9 Kết nối tri thức
Câu “Quýt, cam mười bảy quả tươi” có nghĩa là tổng số cam và số quýt là 17. Hãy viết hệ thức với hai biến x và y biểu thị giả thiết này.
Phương pháp giải:
Phía trên của câu hỏi đã cho: Gọi x là số cam, y là số quýt ( với x, y nguyên dương)
Tổng số cam và số quýt tức là phép tính cộng x quả quýt và y quả cam
Lời giải chi tiết:
Hệ thức biểu thị: \(x + y = 17.\)
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 6 SGK Toán 9 Kết nối tri thức
Tương tự, hãy viết hệ thức với hai biến x và y biểu thị giả thiết cho bởi các câu thơ thứ ba, thứ tư và thứ năm.
Quýt, cam mười bảy quả tươi
Đem chia cho một trăm người cùng vui.
Chia ba mỗi quả quýt rồi,
Còn cam, mỗi quả chia mười vừa xinh.
Trăm người, trăm miếng ngọt lành.
Quýt, cam mỗi loại tính rành là bao?

Phương pháp giải:
- Câu thơ thứ 3 (Chia ba mỗi quả quýt rồi) tức là mỗi quả quýt thì ta sẽ có 3 miếng nên y quả sẽ có \(3y\) miếng
- Câu thơ thứ tư (Còn cam, mỗi quả chia mười vừa xinh) tức là mỗi quả cam thì ta sẽ có 10 miếng nên x quả sẽ có \(10x\) miếng
- Trăm người trăm miếng tức là số miếng quýt (\(3y\) miếng) và số miếng cam (\(10x\) miếng) tổng là 100 miếng
Lời giải chi tiết:
Hệ thức liên hệ giữa x và y qua các câu thơ thứ ba, thứ tư và thứ năm là \(10x + 3y = 100.\)
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 1 trang 6 SGK Toán 9 Kết nối tri thức
Hãy viết một phương trình bậc nhất hai ẩn và chỉ ra một nghiệm của nó.
Phương pháp giải:
Phương trình bậc nhất hai ẩn x và y là hệ thức dạng \(ax + by = c\left( 1 \right)\) trong đó a,b và c là các số đã biết \(a \ne 0\) hoặc \(b \ne 0.\) Nên ta có thể chọn a, b,c là số thực bất kì.
Nếu thay \(x = {x_0};y = {y_0}\) vào phương trình số \(\left( 1 \right)\) thì ta có \(a{x_0} + b{y_0} = c\) là một khẳng định đúng thì \(\left( {{x_0};{y_0}} \right)\) là nghiệm của phương trình \(\left( 1 \right)\)
Lời giải chi tiết:
Ta có \(2x - y = 5\) là một phương trình bậc nhất hai ẩn.
Cặp số \(\left( {3;1} \right)\) là một nghiệm của phương trình \(2x - y = 5\) vì \(2.3 - 1 = 5.\) (luôn đúng).
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 2 trang 8 SGK Toán 9 Kết nối tri thức
Viết nghiệm và biểu diễn hình học tất cả các nghiệm của mỗi phương trình bậc nhất hai ẩn sau:
a) \(2x - 3y = 5;\)
b) \(0x + y = 3;\)
c) \(x + 0y = - 2.\)
Phương pháp giải:
Để viết nghiệm của một phương trình bậc nhất hai ẩn, ta cần rút y theo x \(\left( {by = c - ax} \right)\) từ đó ta giải được \(y = \frac{{c - ax}}{b}\) với \(b \ne 0.\) Đối với trường hợp \(b = 0\) thì ta làm ngược lại (rút x theo y).
Biểu diễn hình học tất cả các nghiệm của phương trình bậc nhất hai ẩn là đường thẳng \(ax + by = c.\)
Lời giải chi tiết:
a) \(2x - 3y = 5;\)
Ta có \(y = \frac{{2x - 5}}{3}\) nên mỗi cặp số \(\left( x;\frac{{2x - 5}}{3} \right)\) với \(x \in \mathbb{R}\) tùy ý là một nghiệm của phương trình \(2x - 3y = 5.\)
Biểu diễn hình học tất cả các nghiệm của phương trình \(2x - 3y = 5.\)
Cho \(x = 0 \Rightarrow y = \frac{{ - 5}}{3} \Rightarrow A\left( {0;\frac{{ - 5}}{3}} \right)\)
\(y = 0 \Rightarrow x = \frac{5}{2} \Rightarrow B\left( {\frac{5}{2};0} \right)\)
Đường thẳng \(2x - 3y = 5\) đi qua hai điểm A và B
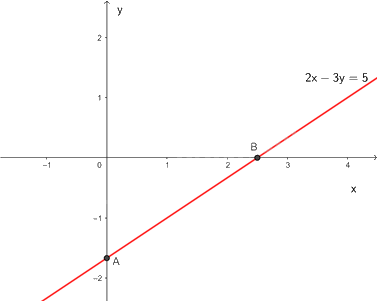
Các nghiệm là tọa độ của một điểm thuộc đường thẳng \(2x - 3y = 5.\)
b) \(0x + y = 3;\)
Ta có \(0x + y = 3\) rút gọn thành \(y = 3\) nên phương trình có nghiệm là \(\left( {x;3} \right)\) với \(x \in \mathbb{R}\) tùy ý.
Mỗi nghiệm này là tọa độ của một điểm thuộc đường thẳng song song với trục hoành và cắt trục tung tại điểm (0;3). Ta gọi đó là đường thẳng y = 3
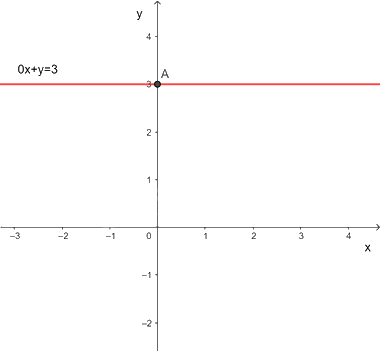
Các nghiệm là tọa độ của một điểm thuộc đường thẳng \(0x + y = 3.\)
c) \(x + 0y = - 2.\)
Ta có \(x + 0y = - 2\) rút gọn thành \(x = - 2\) nên phương trình có nghiệm là \(\left( { - 2;y} \right)\) với \(y \in \mathbb{R}\) tùy ý.
Mỗi nghiệm này là tọa độ của một điểm thuộc đường thẳng song song với trục tung và cắt trục hoành tại điểm (-2; 0). Ta gọi đó là đường thẳng x = -2
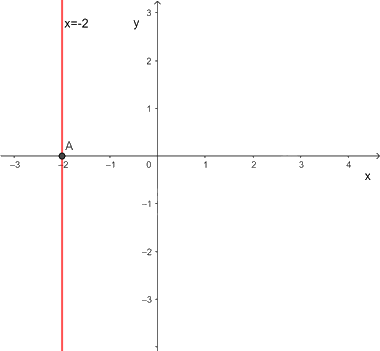
Các nghiệm là tọa độ của một điểm thuộc đường thẳng \(x + 0y = - 2.\)
Mục 1 của chương trình Toán 9 tập 1 Kết nối tri thức tập trung vào việc ôn tập và hệ thống hóa kiến thức về căn bậc hai và căn bậc ba. Đây là nền tảng quan trọng để học sinh tiếp cận các kiến thức nâng cao hơn trong chương trình. Việc nắm vững các khái niệm, tính chất và phương pháp giải bài tập trong mục này là vô cùng cần thiết.
Mục 1 bao gồm các nội dung sau:
Dưới đây là hướng dẫn giải chi tiết các bài tập trong mục 1 trang 6, 7, 8 SGK Toán 9 tập 1 Kết nối tri thức:
Bài tập này yêu cầu học sinh tìm hiểu về điều kiện xác định của căn bậc hai. Để giải bài tập này, học sinh cần nhớ rằng căn bậc hai của một số thực chỉ xác định khi số đó lớn hơn hoặc bằng 0.
Bài tập này yêu cầu học sinh tính giá trị của các biểu thức chứa căn bậc hai. Để giải bài tập này, học sinh cần sử dụng các tính chất của căn bậc hai và thực hiện các phép toán một cách chính xác.
Bài tập này yêu cầu học sinh so sánh các số thực bằng cách sử dụng căn bậc hai. Để giải bài tập này, học sinh cần biến đổi các số thực về dạng căn bậc hai và so sánh chúng.
Bài tập này yêu cầu học sinh giải các bài toán thực tế liên quan đến căn bậc hai. Để giải bài tập này, học sinh cần phân tích đề bài, xác định các yếu tố liên quan đến căn bậc hai và xây dựng phương trình để giải.
Bài tập này yêu cầu học sinh vận dụng kiến thức về căn bậc ba để giải quyết các vấn đề thực tế. Học sinh cần hiểu rõ định nghĩa và tính chất của căn bậc ba để áp dụng vào giải bài tập.
Khi giải bài tập về căn bậc hai và căn bậc ba, học sinh cần lưu ý những điều sau:
Ví dụ 1: Tính giá trị của biểu thức √(16) + ∛(8)
Giải:
Ví dụ 2: So sánh hai số thực √2 và ∛3
Giải:
Việc nắm vững kiến thức về căn bậc hai và căn bậc ba là vô cùng quan trọng đối với học sinh lớp 9. Hy vọng rằng với hướng dẫn chi tiết và các ví dụ minh họa trên, các em học sinh sẽ tự tin hơn trong việc giải các bài tập trong mục 1 trang 6, 7, 8 SGK Toán 9 tập 1 Kết nối tri thức. Chúc các em học tập tốt!