Bài tập 9.31 trang 91 SGK Toán 9 tập 2 thuộc chương trình Toán 9 Kết nối tri thức, yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế. Bài tập này thường gặp trong các kỳ thi và kiểm tra, do đó việc nắm vững phương pháp giải là vô cùng quan trọng.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 9.31 trang 91 SGK Toán 9 tập 2, giúp các em học sinh hiểu rõ bản chất của bài toán và tự tin giải các bài tập tương tự.
Cho tam giác ABC có các đường cao AD, BE, CF. Chứng minh rằng BCEF, CAFD, ABDE là những tứ giác nội tiếp.
Đề bài
Cho tam giác ABC có các đường cao AD, BE, CF. Chứng minh rằng BCEF, CAFD, ABDE là những tứ giác nội tiếp.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+ Chứng minh bốn điểm B, F, E, C thuộc đường tròn đường kính BC nên tứ giác BCEF là tứ giác nội tiếp.
+ Chứng minh bốn điểm C, A, F, D thuộc đường tròn đường kính AC nên tứ giác CAFD là tứ giác nội tiếp.
+ Chứng minh bốn điểm B, A, E, D thuộc đường tròn đường kính BA nên tứ giác ABDE là tứ giác nội tiếp.
Lời giải chi tiết
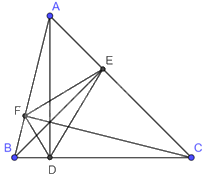
Vì AD, BE, CF là các đường cao của tam giác ABC nên \(AD \bot BC,BE \bot AC,CF \bot AB\).
Do đó, \(\widehat {ADB} \) \(= \widehat {ADC} \) \(= \widehat {BEC} \) \(= \widehat {BEA} \) \(= \widehat {AFC} \) \(= \widehat {CFB} \) \(= {90^o}\).
Vì \(\widehat {BFC} = \widehat {BEC} = {90^o}\) nên tam giác BFC vuông tại F và tam giác BEC vuông tại E. Do đó, hai điểm E, F thuộc đường tròn đường kính BC. Do đó, tứ giác BCEF là tứ giác nội tiếp.
Vì \(\widehat {AFC} = \widehat {ADC} = {90^o}\) nên tam giác AFC vuông tại F và tam giác ADC vuông tại D. Do đó, hai điểm D, F thuộc đường tròn đường kính AC. Do đó, tứ giác CAFD là tứ giác nội tiếp.
Vì \(\widehat {ADB} = \widehat {AEB} = {90^o}\) nên tam giác ADB vuông tại D và tam giác AEB vuông tại E. Do đó, hai điểm E, D thuộc đường tròn đường kính BA. Do đó, tứ giác ABDE là tứ giác nội tiếp.
Bài tập 9.31 trang 91 SGK Toán 9 tập 2 yêu cầu học sinh giải một bài toán thực tế liên quan đến hàm số bậc hai. Để giải bài tập này, chúng ta cần nắm vững các kiến thức sau:
Đề bài: (Giả sử đề bài là một bài toán cụ thể về quỹ đạo vật được ném, hoặc một bài toán tối ưu hóa liên quan đến hàm số bậc hai. Ví dụ: Một quả bóng được ném lên từ mặt đất với vận tốc ban đầu là 15 m/s. Hãy tìm độ cao lớn nhất mà quả bóng đạt được.)
Lời giải:
Kết luận: Độ cao lớn nhất mà quả bóng đạt được là khoảng 11.48 mét.
Ngoài bài tập 9.31, còn rất nhiều bài tập tương tự liên quan đến hàm số bậc hai. Các bài tập này thường yêu cầu học sinh:
Để giải các bài tập này, học sinh cần nắm vững các kiến thức về hàm số bậc hai và luyện tập thường xuyên. Giaitoan.edu.vn cung cấp nhiều bài tập luyện tập khác nhau với các mức độ khó khác nhau, giúp các em học sinh củng cố kiến thức và nâng cao kỹ năng giải toán.
Khi giải bài tập về hàm số bậc hai, học sinh cần lưu ý những điều sau:
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên, các em học sinh sẽ tự tin giải bài tập 9.31 trang 91 SGK Toán 9 tập 2 - Kết nối tri thức và các bài tập tương tự. Chúc các em học tốt!
| Kiến thức | Nội dung |
|---|---|
| Định nghĩa | Hàm số bậc hai có dạng y = ax2 + bx + c, với a ≠ 0. |
| Đồ thị | Đồ thị của hàm số bậc hai là một parabol. |
| Hoành độ đỉnh | x = -b / (2a) |
| Tung độ đỉnh | y = -Δ / (4a) (với Δ = b2 - 4ac) |