Chào mừng bạn đến với bài học về lý thuyết Cung và dây của đường tròn trong chương trình Toán 9 Kết nối tri thức. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về cung, dây cung, mối quan hệ giữa chúng và các tính chất liên quan.
Chúng ta sẽ cùng nhau khám phá định nghĩa, tính chất của cung và dây, cách xác định độ dài cung và dây, cũng như ứng dụng của lý thuyết này trong giải các bài toán hình học.
1. Dây và đường kính của đường tròn Khái niệm dây
1. Dây và đường kính của đường tròn
Khái niệm dây
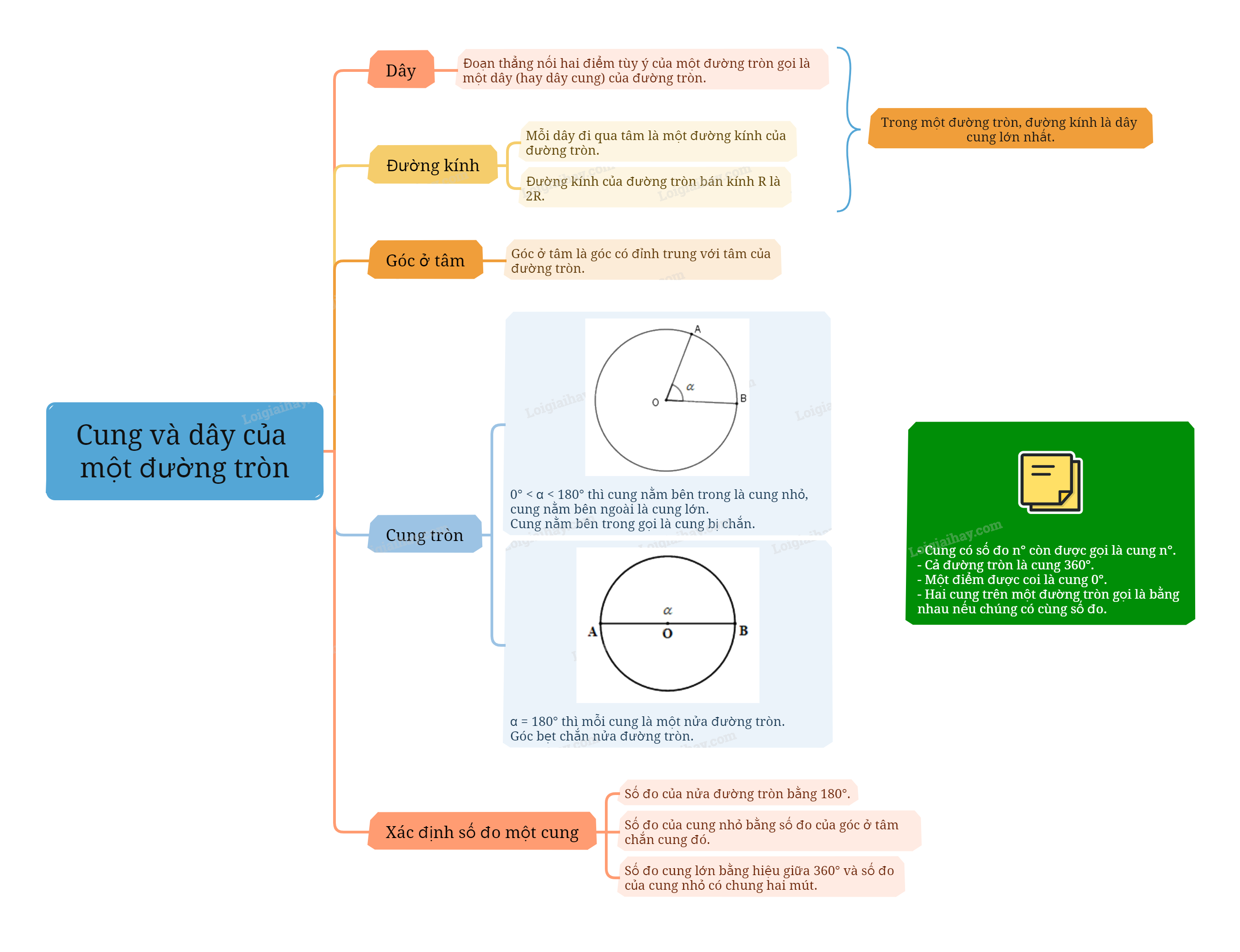
Đoạn thẳng nối hai điểm tùy ý của một đường tròn gọi là một dây (hay dây cung) của đường tròn.
Khái niệm đường kính của đường tròn
Mỗi dây đi qua tâm là một đường kính của đường tròn.
Đường kính của đường tròn bán kính R là 2R.
Ví dụ:
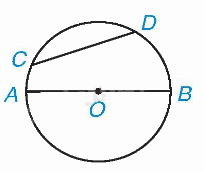
Trong hình trên, CD là một dây, AB là một đường kính của (O).
Quan hệ giữa dây và đường kính
Trong một đường tròn, đường kính là dây cung lớn nhất. |
2. Góc ở tâm, cung và số đo của một cung
Khái niệm góc ở tâm và cung tròn
Góc ở tâm là góc có đỉnh trùng với tâm của đường tròn. |
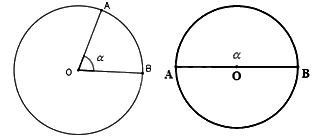
- Nếu \({0^0} < \alpha < {180^0}\) thì cung nằm bên trong góc được gọi là cung nhỏ, cung nằm bên ngoài góc được gọi là cung lớn.
- Nếu \(\alpha = {180^0}\) thì mỗi cung là một nửa đường tròn.
- Cung nằm bên trong gọi là cung bị chắn. Góc bẹt chắn nửa đường tròn.
Ví dụ:
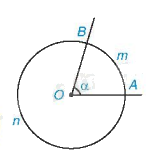
Trong hình trên, $\overset\frown{AmO}$ là cung nhỏ, ta có thể kí hiệu gọn là \(\overset\frown{AB}\).
$\overset\frown{AnB}$ là cung lớn.
Ta nói góc AOB chắn cung AB hay cung AB bị chắn bởi góc AOB.
Cách xác định số đo một cung
Số đo của một cung được xác định như sau:
- Số đo của nửa đường tròn bằng \({180^0}\).
- Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.
- Số đo cung lớn bằng hiệu giữa \({360^0}\) và số đo của cung nhỏ có chung hai mút.
Ví dụ: Số đo của cung AB được kí hiệu là sđ$\overset\frown{AB}$.
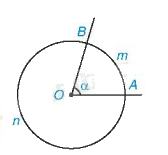
sđ$\overset\frown{AmB}=\widehat{AOB}=\alpha $; sđ$\overset\frown{AnB}={{360}^{0}}-\alpha $.
Chú ý:
- Cung có số đo \({n^0}\) còn được gọi là cung \({n^0}\). Cả đường tròn được coi là cung \({360^0}\). Đôi khi ta cũng coi một điểm là cung \({0^0}\).
- Hai cung trên một đường tròn gọi là bằng nhau nếu chúng có cùng số đo.
Trong chương trình Hình học lớp 9, kiến thức về đường tròn đóng vai trò vô cùng quan trọng. Một trong những nội dung cốt lõi của chương này là lý thuyết về cung và dây của đường tròn. Bài viết này sẽ trình bày chi tiết lý thuyết này theo chương trình Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và áp dụng vào giải bài tập một cách hiệu quả.
Cung tròn: Cung tròn là một phần của đường tròn giới hạn bởi hai điểm trên đường tròn. Hai điểm này được gọi là mút cung.
Dây cung: Dây cung là đoạn thẳng nối hai điểm trên đường tròn. Dây cung đi qua tâm đường tròn được gọi là đường kính.
Số đo cung: Số đo cung là số đo của góc ở tâm chắn cung đó. Ví dụ, cung AB có số đo bằng số đo của góc AOB (O là tâm đường tròn).
Tính chất 1: Trong một đường tròn, cung lớn hơn thì dây cung tương ứng cũng lớn hơn.
Tính chất 2: Trong một đường tròn, hai dây cung bằng nhau thì hai cung tương ứng bằng nhau.
Tính chất 3: Trong một đường tròn, hai cung bằng nhau thì hai dây cung tương ứng bằng nhau.
Định lý 1: Đường thẳng đi qua tâm của một đường tròn và vuông góc với một dây cung thì chia đôi dây cung đó.
Định lý 2: Đường thẳng chia đôi một dây cung của đường tròn thì vuông góc với dây cung đó tại trung điểm của nó.
Hệ quả: Đường trung trực của một dây cung đi qua tâm của đường tròn.
Độ dài cung tròn được tính theo công thức:
l = πrn
Trong đó:
Bài 1: Cho đường tròn (O) có bán kính 5cm. Tính độ dài cung 60o.
Giải:
Độ dài cung 60o là: l = π * 5 * (60/180) = (5π)/3 cm.
Bài 2: Cho đường tròn (O) có dây cung AB = 8cm. Khoảng cách từ O đến AB là 3cm. Tính bán kính của đường tròn.
Giải:
Gọi M là trung điểm của AB. Khi đó OM vuông góc với AB và AM = MB = 4cm. Áp dụng định lý Pitago vào tam giác OMA, ta có:
OA2 = OM2 + AM2 = 32 + 42 = 25
Suy ra OA = 5cm. Vậy bán kính của đường tròn là 5cm.
Lý thuyết về cung và dây của đường tròn là nền tảng quan trọng để hiểu và giải quyết các bài toán liên quan đến đường tròn trong chương trình Toán 9. Việc nắm vững các định nghĩa, tính chất và công thức liên quan sẽ giúp các em học sinh tự tin hơn trong quá trình học tập và làm bài tập.