Chào mừng các em học sinh đến với lời giải chi tiết bài tập 9.7 trang 76 SGK Toán 9 tập 2 - Kết nối tri thức. Bài tập này thuộc chương trình học Toán 9, tập trung vào việc vận dụng kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn cung cấp lời giải dễ hiểu, chi tiết, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Cho đường tròn (O) ngoại tiếp tam giác ABC. Tính bán kính của (O), biết rằng tam giác ABC vuông cân tại A và có cạnh bên bằng (2sqrt 2 cm).
Đề bài
Cho đường tròn (O) ngoại tiếp tam giác ABC. Tính bán kính của (O), biết rằng tam giác ABC vuông cân tại A và có cạnh bên bằng \(2\sqrt 2 cm\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+ Áp dụng định lí Pythagore vào tam giác ABC vuông tại A tính BC.
+ Vì O là trung điểm của BC nên \(OB = OC = \frac{{BC}}{2}\) là bán kính đường tròn (O) ngoại tiếp tam giác ABC.
Lời giải chi tiết
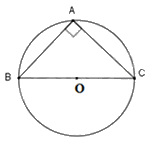
Tam giác ABC vuông cân tại A nên \(AB = AC = 2\sqrt 2 cm\)
Áp dụng định lí Pythagore vào tam giác ABC vuông tại A ta có:
\(B{C^2} = A{B^2} + A{C^2} = {\left( {2\sqrt 2 } \right)^2} + {\left( {2\sqrt 2 } \right)^2} = 16 \) suy ra \(BC = 4cm\)
Vì O là trung điểm của BC nên \(OB = OC = \frac{{BC}}{2} = \frac{4}{2} = 2\left( {cm} \right)\)
Vì tam giác ABC vuông tại A nên tam giác ABC nội tiếp đường tròn tâm O, bán kính OC.
Vậy bán kính đường tròn (O) ngoại tiếp tam giác ABC bằng 2cm.
Bài tập 9.7 trang 76 SGK Toán 9 tập 2 - Kết nối tri thức là một bài toán quan trọng, yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai và các tính chất của đồ thị hàm số để giải quyết. Dưới đây là hướng dẫn chi tiết từng bước để các em có thể hiểu rõ cách giải bài tập này.
Trước khi bắt đầu giải bài tập, chúng ta cần phân tích kỹ đề bài để xác định rõ yêu cầu và các thông tin đã cho. Bài tập 9.7 thường yêu cầu học sinh xác định phương trình của đường thẳng, parabol hoặc tìm giao điểm của chúng.
Giả sử bài tập 9.7 yêu cầu tìm giao điểm của parabol (P): y = x2 - 4x + 3 và đường thẳng (d): y = -x + 3.
Giải:
Để tìm giao điểm, ta giải phương trình:
x2 - 4x + 3 = -x + 3
x2 - 3x = 0
x(x - 3) = 0
Vậy x = 0 hoặc x = 3.
Với x = 0, y = -0 + 3 = 3. Vậy giao điểm thứ nhất là A(0; 3).
Với x = 3, y = -3 + 3 = 0. Vậy giao điểm thứ hai là B(3; 0).
Kết luận: Parabol (P) và đường thẳng (d) cắt nhau tại hai điểm A(0; 3) và B(3; 0).
Để củng cố kiến thức, các em có thể tự giải các bài tập tương tự trong SGK Toán 9 tập 2 - Kết nối tri thức hoặc các đề thi thử.
Kiến thức về hàm số bậc hai và các tính chất của đồ thị hàm số có ứng dụng rộng rãi trong thực tế, như trong việc thiết kế các công trình kiến trúc, tính toán quỹ đạo của vật thể, và phân tích các hiện tượng tự nhiên.
Bài tập 9.7 trang 76 SGK Toán 9 tập 2 - Kết nối tri thức là một bài tập quan trọng, giúp các em rèn luyện kỹ năng giải toán và vận dụng kiến thức đã học. Hy vọng với hướng dẫn chi tiết này, các em sẽ tự tin hơn trong quá trình học tập và đạt kết quả tốt.
| Công thức quan trọng | Mô tả |
|---|---|
| Phương trình đường thẳng | y = ax + b |
| Phương trình parabol | y = ax2 + bx + c |
| Hoành độ giao điểm | ax2 + bx + c = mx + n |
| Nguồn: SGK Toán 9 tập 2 - Kết nối tri thức | |