Bài tập 7.28 trang 55 SGK Toán 9 tập 2 thuộc chương trình Toán 9 Kết nối tri thức, yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế. Bài tập này thường gặp trong các kỳ thi và kiểm tra, do đó việc nắm vững phương pháp giải là vô cùng quan trọng.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 7.28 trang 55 SGK Toán 9 tập 2, giúp các em học sinh hiểu rõ bản chất của bài toán và tự tin giải các bài tập tương tự.
Tỉ lệ học sinh bình chọn cho danh hiệu cầu thủ xuất sắc nhất trong giải bóng đá của trường được cho trong bảng sau: Biết rằng có 500 học sinh tham gia bình chọn. a) Vẽ biểu đồ hình quạt tròn biểu diễn bảng tần số tương đối trên. b) Lập bảng tần số biểu diễn số học sinh bình chọn cho danh hiệu cầu thủ xuất sắc nhất trong giải bóng đá của trường.
Đề bài
Tỉ lệ học sinh bình chọn cho danh hiệu cầu thủ xuất sắc nhất trong giải bóng đá của trường được cho trong bảng sau:

Biết rằng có 500 học sinh tham gia bình chọn.
a) Vẽ biểu đồ hình quạt tròn biểu diễn bảng tần số tương đối trên.
b) Lập bảng tần số biểu diễn số học sinh bình chọn cho danh hiệu cầu thủ xuất sắc nhất trong giải bóng đá của trường.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Cách vẽ biểu đồ tần số tương đối hình quạt tròn:
Bước 1: Xác định số đo cung tương ứng của các hình quạt dùng để biểu diễn tần số tương đối của các giá trị theo công thức \({360^o}.{f_i}\) với \(i = 1,...,k\).
Bước 2: Vẽ hình tròn và chia hình tròn thành các hình quạt có số đo cung tương ứng được xác định trong Bước 1.
Bước 3: Định dạng các hình quạt tròn (thường bằng cách tô màu), ghi tần số tương đối, chú giải và tiêu đề.
b) Tần số bình chọn cho mỗi cầu thủ là: 500. Tỉ lệ học sinh bình chọn (học sinh)
Lời giải chi tiết
a) Bước 1: Xác định số đo cung tương ứng của các hình quạt biểu diễn các tần số tương đối của tỉ lệ bình chọn cầu thủ xuất sắc nhất:
Huy: \({360^o}.30\% = {108^o}\), Minh: \({360^o}.25\% = {90^o}\), An: \({360^o}.10\% = {36^o}\), Thảo: \({360^o}.35\% = {126^o}\).
Bước 2: Vẽ hình tròn và chia hình tròn thành các hình quạt.
Bước 3: Định dạng các hình quạt tròn, ghi tần số tương đối, chú giải và tiêu đề.
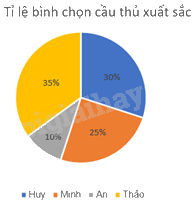
b) Số học sinh bình chọn Huy là cầu thủ xuất sắc nhất là: \(500.30\% = 150\) (học sinh)
Số học sinh bình chọn Minh là cầu thủ xuất sắc nhất là: \(500.25\% = 125\) (học sinh)
Số học sinh bình chọn An là cầu thủ xuất sắc nhất là: \(500.10\% = 50\) (học sinh)
Số học sinh bình chọn Thảo là cầu thủ xuất sắc nhất là: \(500.35\% = 175\) (học sinh)
Ta có bảng tần số biểu diễn số học sinh bình chọn cho danh hiệu cầu thủ xuất sắc nhất trong giải bóng đá của trường là:

Bài tập 7.28 trang 55 SGK Toán 9 tập 2 yêu cầu học sinh giải một bài toán thực tế liên quan đến hàm số bậc hai. Để giải bài tập này, chúng ta cần nắm vững các kiến thức sau:
Đề bài: (Giả sử đề bài là một bài toán cụ thể về quỹ đạo vật thể được ném lên, hoặc một bài toán tối ưu hóa liên quan đến hàm số bậc hai. Ví dụ: Một quả bóng được ném lên từ mặt đất với vận tốc ban đầu là 15m/s. Hãy tìm độ cao lớn nhất mà quả bóng đạt được.)
Bước 1: Xác định hàm số bậc hai mô tả bài toán.
Trong bài toán này, độ cao của quả bóng theo thời gian có thể được mô tả bằng hàm số bậc hai có dạng:
h(t) = -1/2 * g * t^2 + v0 * t + h0
Trong đó:
Thay các giá trị vào, ta được hàm số:
h(t) = -4.9 * t^2 + 15 * t
Bước 2: Tìm tọa độ đỉnh của đồ thị hàm số.
Tọa độ đỉnh của đồ thị hàm số h(t) = at^2 + bt + c là:
(t_đỉnh, h_đỉnh) = (-b / 2a, -Δ / 4a)
Trong đó Δ = b^2 - 4ac.
Áp dụng vào hàm số h(t) = -4.9 * t^2 + 15 * t, ta có:
a = -4.9, b = 15, c = 0
Δ = 15^2 - 4 * (-4.9) * 0 = 225
t_đỉnh = -15 / (2 * -4.9) ≈ 1.53 s
h_đỉnh = -225 / (4 * -4.9) ≈ 11.48 m
Bước 3: Kết luận.
Vậy độ cao lớn nhất mà quả bóng đạt được là khoảng 11.48 mét.
Khi giải các bài toán liên quan đến hàm số bậc hai, cần chú ý các bước sau:
Ngoài ra, các em học sinh có thể tham khảo thêm các bài giảng và tài liệu học tập về hàm số bậc hai để nắm vững kiến thức và rèn luyện kỹ năng giải bài tập.
Giaitoan.edu.vn hy vọng với lời giải chi tiết này, các em học sinh sẽ hiểu rõ hơn về cách giải bài tập 7.28 trang 55 SGK Toán 9 tập 2 - Kết nối tri thức và tự tin hơn trong việc học tập môn Toán.
Các bài tập tương tự có thể được tìm thấy trên trang web giaitoan.edu.vn, hãy truy cập để luyện tập và nâng cao kiến thức của bạn.