Bài tập 9.34 trang 91 SGK Toán 9 tập 2 thuộc chương trình Toán 9 Kết nối tri thức, yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế. Bài viết này sẽ cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Giaitoan.edu.vn luôn đồng hành cùng các em học sinh trên con đường chinh phục môn Toán. Chúng tôi cung cấp đầy đủ các bài giải SGK Toán 9, bài tập trắc nghiệm, và các tài liệu học tập hữu ích khác.
Biết rằng bốn đỉnh A, B, C, D của một hình vuông cùng nằm trên một đường tròn (O) theo thứ tự ngược chiều kim đồng hồ. Phép quay thuận chiều ({45^o}) biến các điểm A, B, C, D lần lượt thành các điểm E, F, G, H. a) Vẽ đa giác EAFBGCHD. b) Đa giác EAFBGCHD có phải là một hình bát giác đều hay không? Vì sao?
Đề bài
Biết rằng bốn đỉnh A, B, C, D của một hình vuông cùng nằm trên một đường tròn (O) theo thứ tự ngược chiều kim đồng hồ. Phép quay thuận chiều \({45^o}\) biến các điểm A, B, C, D lần lượt thành các điểm E, F, G, H.
a) Vẽ đa giác EAFBGCHD.
b) Đa giác EAFBGCHD có phải là một hình bát giác đều hay không? Vì sao?
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) + Vẽ đường tròn (O). Trên đường tròn vẽ hình vuông ABCD sao cho các đỉnh A, B, C, D theo thứ tự ngược chiều kim đồng hồ.
+ Vẽ điểm E thuộc đường tròn (O) sao cho \(\widehat {AOE} = {45^o}\) và tia OA quay thuận theo chiều kim đồng hồ đến tia OE.
+ Xác định các điểm F, G, H tương tự như xác định điểm E. Nối A với E, E với D, D với H, H với C, C với G, G với B, B với F, F với A ta được đa giác EAFBGCHD.
b) Chứng minh \(AE = ED = DH = HC = CG = BG = BF = FA\) và \(\widehat {FAE} = \widehat {AED} = \widehat {EDH} = \widehat {DHC} = \widehat {HCG} = \widehat {CGB} = \widehat {GBF} = \widehat {BFA}\) nên đa giác EAFBGCHD là bát giác đều.
Lời giải chi tiết
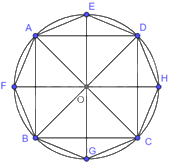
a) + Vẽ đường tròn (O). Trên đường tròn vẽ hình vuông ABCD sao cho các đỉnh A, B, C, D theo thứ tự ngược chiều kim đồng hồ.
+ Vẽ điểm E thuộc đường tròn (O) sao cho \(\widehat {AOE} = {45^o}\) và tia OA quay thuận theo chiều kim đồng hồ đến tia OE.
+ Xác định các điểm F, G, H tương tự như xác định điểm E. Nối A với E, E với D, D với H, H với C, C với G, G với B, B với F, F với A ta được đa giác EAFBGCHD.
b) Vì A, E, D, H, C, G, B, F cùng thuộc (O) nên
\(OA = OE = OD = OH = OC = OG = OB = OF\)
Vì ABCD là hình vuông nên
\(\widehat {AOD} = \widehat {DOC} = \widehat {BOC} = \widehat {BOA} = {90^o}\)
Lại có: \(\widehat {AOE} = \widehat {BOF} = \widehat {COG} = \widehat {DOH} = {45^o}\) nên \(\widehat {DOE} = \widehat {AOF} = \widehat {BOG} = \widehat {COH} = {45^o}\)
Ta có:
\(\Delta AOE = \Delta DOE = \Delta DOH = \Delta COH = \Delta COG = \Delta BOG = \Delta BOF = \Delta AOF\left( {c.g.c} \right)\)
Suy ra:
+) \(AE = ED = DH = HC = CG = BG = BF = FA\)
+) \(\widehat {OAE} = \widehat {OEA} = \widehat {OED} = \widehat {ODE} = \widehat {ODH} = \widehat {OHD} = \widehat {OHC} = \widehat {OCH} = \widehat {OCG} = \widehat {OGC} = \widehat {OGB} = \widehat {OBG}\)\( = \widehat {OBF} = \widehat {OFB} = \widehat {OFA} = \widehat {FAO}\)
Do đó, \(\widehat {FAE} = \widehat {AED} = \widehat {EDH} = \widehat {DHC} = \widehat {HCG} = \widehat {CGB} = \widehat {GBF} = \widehat {BFA}\)
Đa giác EAFBGCHD có
\(\widehat {FAE} = \widehat {AED} = \widehat {EDH} = \widehat {DHC} = \widehat {HCG} = \widehat {CGB} = \widehat {GBF} = \widehat {BFA}\) và \(AE = ED = DH = HC = CG = BG = BF = FA\) nên đa giác EAFBGCHD là hình bát giác đều.
Bài tập 9.34 SGK Toán 9 tập 2 Kết nối tri thức yêu cầu học sinh giải một bài toán thực tế liên quan đến hàm số bậc hai. Để giải bài tập này, chúng ta cần xác định được hàm số bậc hai phù hợp với dữ kiện đề bài, sau đó tìm các hệ số của hàm số và giải các phương trình tương ứng.
Trước khi bắt tay vào giải bài tập, chúng ta cần đọc kỹ đề bài và phân tích các thông tin được cung cấp. Từ đó, xác định được các yếu tố quan trọng như các điểm mà đồ thị hàm số đi qua, trục đối xứng của đồ thị, hoặc đỉnh của đồ thị. Dựa trên các yếu tố này, chúng ta có thể xác định được dạng tổng quát của hàm số bậc hai: y = ax2 + bx + c.
Sau khi xác định được dạng tổng quát của hàm số, chúng ta cần tìm các hệ số a, b, c. Để làm điều này, chúng ta có thể sử dụng các điểm mà đồ thị hàm số đi qua. Thay tọa độ của các điểm này vào phương trình hàm số, chúng ta sẽ có một hệ phương trình bậc hai với ba ẩn a, b, c. Giải hệ phương trình này, chúng ta sẽ tìm được giá trị của các hệ số a, b, c.
Sau khi tìm được các hệ số a, b, c, chúng ta có thể viết được phương trình hàm số bậc hai cụ thể. Dựa trên phương trình này, chúng ta có thể giải các phương trình tương ứng để tìm ra các giá trị cần thiết của bài toán. Ví dụ, chúng ta có thể tìm ra nghiệm của phương trình bậc hai, hoặc tìm ra tọa độ của đỉnh của đồ thị hàm số.
Giả sử đề bài yêu cầu tìm phương trình đường thẳng đi qua hai điểm A(1; 2) và B(3; 8). Chúng ta có thể làm như sau:
Hàm số bậc hai có rất nhiều ứng dụng trong thực tế, ví dụ như:
Bài tập 9.34 trang 91 SGK Toán 9 tập 2 Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc hai. Hy vọng với hướng dẫn chi tiết trên, các em học sinh sẽ tự tin giải bài tập và đạt kết quả tốt trong môn Toán.
Giaitoan.edu.vn luôn cập nhật các bài giải mới nhất và cung cấp các tài liệu học tập hữu ích cho học sinh. Hãy truy cập website của chúng tôi để được hỗ trợ tốt nhất!