Bài tập 9.17 trang 79 SGK Toán 9 tập 2 thuộc chương trình Toán 9 Kết nối tri thức, yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế. Bài viết này sẽ cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Giaitoan.edu.vn luôn đồng hành cùng các em học sinh trên con đường chinh phục môn Toán. Chúng tôi cung cấp đầy đủ các lời giải bài tập, lý thuyết và các bài toán nâng cao để giúp các em học tập hiệu quả.
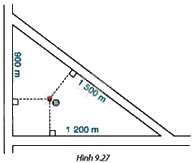
Người ta vẽ bản quy hoạch của một khu định cư được bao xung quanh bởi ba con đường thẳng lập thành một tam giác với độ dài các cạnh là 900m, 1 200m và 1 500m (H.9.27). a) Tính chu vi và diện tích của phần đất giới hạn bởi tam giác trên. b) Họ muốn xây dựng một khách sạn bên trong khu dân cư cách đều cả ba con đường đó. Hỏi khi đó khách sạn sẽ cách mỗi con đường một khoảng là bao nhiêu?
Đề bài
Người ta vẽ bản quy hoạch của một khu định cư được bao xung quanh bởi ba con đường thẳng lập thành một tam giác với độ dài các cạnh là 900m, 1 200m và 1 500m (H.9.27).
a) Tính chu vi và diện tích của phần đất giới hạn bởi tam giác trên.
b) Họ muốn xây dựng một khách sạn bên trong khu dân cư cách đều cả ba con đường đó. Hỏi khi đó khách sạn sẽ cách mỗi con đường một khoảng là bao nhiêu?
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) + Chu vi phần đất giới hạn bởi tam giác trên là tổng của ba cạnh tam giác.
+ Chứng minh phần đất giới hạn bởi tam giác là tam giác vuông.
+ Khi đó, diện tích phần đất giới hạn bởi tam giác đó bằng nửa tích hai cạnh góc vuông.
b) Gọi tam giác giới hạn phần đất là ABC, trong đó \(AB = 900m,\;AC = 1200m,\;BC = 1500m\).
+ Khách sạn nằm ở vị trí tâm đường tròn nội tiếp tam giác ABC.
+ Từ I kẻ ID vuông góc với AB tại D, IE vuông góc với AC tại E, IF vuông góc với BC.
+ Chứng minh tứ giác AEID là hình vuông.
+ Đặt ID = IE = AE = DA = r.
+ Sử dụng tính chất của hai tiếp tuyến cắt nhau để tìm r
Lời giải chi tiết
a) Vì \({900^2} + 1\;{200^2} = 1\;{500^2}\) nên tam giác này là tam giác vuông.
Diện tích phần đất giới hạn bởi tam giác trên là:
\(S = \frac{1}{2}.900.1\;200 = 540\;000\left( {{m^2}} \right)\)
Chu vi phần đất giới hạn bởi tam giác trên là:
\(900 + 1\;200 + 1\;500 = 3\;600\left( m \right)\)
b) Để khách sạn cách đều cả ba con đường thì khách sạn đó trùng với tâm đường tròn nội tiếp tam giác giới hạn phần đất.
Gọi tam giác giới hạn phần đất là ABC, trong đó, \(AB = 900m,\;AC = 1200m,\;BC = 1500m\).
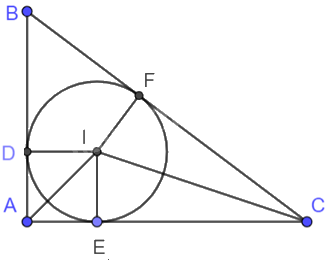
Do đó, tam giác ABC vuông tại A. Gọi I là tâm đường tròn nội tiếp tam giác ABC.
Từ I kẻ ID vuông góc với AB tại D, IE vuông góc với AC tại E, IF vuông góc với BC tại F.
Khi đó, \(ID = IE = IF\).
Vì ID vuông góc với AB tại D, IE vuông góc với AC tại E nên \(\widehat {IEA} = \widehat {IDA} = {90^o}\).
Tứ giác ADIE có: \(\widehat {EAD} = \widehat {IEA} = \widehat {IDA} = {90^o}\) nên tứ giác ADIE là hình chữ nhật. Mà \(ID = IE\) nên tứ giác ADIE là hình vuông.
Do đó, \(ID = IE = AE = AD = r\)
Ta có: \(EC = AC - AE = 1200 - AE = 1200 - r\), \(BD = AB - AD = 900 - r\)
Vì CE và CF là hai tiếp tuyến cắt nhau của (O) nên CE = CF.
Vì BF và BA là hai tiếp tuyến cắt nhau của (O) nên BD = BF.
Mà BF + CF = BC = 1500 nên ta có:
\(900 - r + 1200 - r = 1500\)
\(2100 - 2r = 1500\)
\(2r = 600\)
\(r = 300\)
Do đó, khách sạn cách mỗi con đường 300m.
Bài tập 9.17 SGK Toán 9 tập 2 Kết nối tri thức là một bài toán ứng dụng thực tế, yêu cầu học sinh sử dụng kiến thức về hàm số bậc hai để giải quyết. Để giải bài tập này, chúng ta cần nắm vững các khái niệm cơ bản về hàm số bậc hai, bao gồm:
Trước khi bắt đầu giải bài tập, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Bài tập 9.17 thường yêu cầu chúng ta:
(Nội dung lời giải chi tiết bài tập 9.17 sẽ được trình bày tại đây, bao gồm các bước giải cụ thể, các công thức sử dụng và các giải thích rõ ràng. Ví dụ:)
Ví dụ: Giả sử đề bài yêu cầu tìm quỹ đạo của một vật được ném lên từ mặt đất với vận tốc ban đầu v0 và góc ném α. Chúng ta có thể sử dụng hàm số bậc hai để mô tả quỹ đạo này.
Phương trình quỹ đạo có dạng: y = x * tan(α) - (g * x2) / (2 * v02 * cos2(α))
Trong đó:
Để giải bài tập này, chúng ta cần xác định các giá trị của v0 và α từ dữ kiện đề bài và sau đó thay vào phương trình trên để tìm quỹ đạo của vật.
Ngoài bài tập 9.17, còn rất nhiều bài tập tương tự liên quan đến hàm số bậc hai. Một số dạng bài tập phổ biến bao gồm:
Để giải các bài tập này, chúng ta cần nắm vững các kiến thức về hàm số bậc hai, các công thức liên quan và các phương pháp giải toán. Ngoài ra, việc luyện tập thường xuyên cũng rất quan trọng để nâng cao kỹ năng giải toán.
Khi giải bài tập về hàm số bậc hai, chúng ta cần lưu ý một số điều sau:
Bài tập 9.17 trang 79 SGK Toán 9 tập 2 Kết nối tri thức là một bài toán quan trọng giúp học sinh củng cố kiến thức về hàm số bậc hai. Hy vọng rằng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải quyết bài tập và đạt kết quả tốt trong môn Toán.
Giaitoan.edu.vn sẽ tiếp tục cập nhật và cung cấp các lời giải bài tập, lý thuyết và các bài toán nâng cao để giúp các em học tập hiệu quả. Chúc các em học tập tốt!