Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tại giaitoan.edu.vn. Chúng tôi xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 1 trang 84, 85, 86 sách giáo khoa Toán 9 tập 2 - Kết nối tri thức.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Ta đã biết các tam giác đều và hình vuông có các đỉnh nằm trên một đường tròn. Ta dựng một đa giác lồi 5 cạnh có các đỉnh nằm trên một đường tròn như sau: - Vẽ đường tròn tâm O bán kính R. - Lần lượt lấy các điểm A, B, C, D, E trên đường tròn theo thứ tự ngược chiều kim đồng hồ (hoặc theo chiều kim đồng hồ) sao cho: (widehat {AOB} = widehat {BOC} = widehat {COD} = widehat {DOE} = widehat {EOA} = frac{{{{360}^o}}}{5} = {72^o}). Em hãy giải thích vì sao các cạnh và các góc của đa giác
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 1 trang 86 SGK Toán 9 Kết nối tri thức
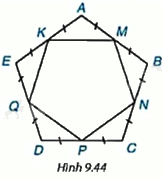
Cho M, N, P, Q, K lần lượt là trung điểm của các cạnh AB, BC, CD, DE và EA của ngũ giác đều ABCDE (H.9.44). Hỏi MNPQK có phải là ngũ giác đều hay không?
Phương pháp giải:
+ Chứng minh \(\Delta AMK = \Delta BMN = \Delta CPN = \Delta DPQ = \Delta EKQ\left( {c.g.c} \right)\) nên \(KM = MN = PN = PQ = QK\).
+ Chứng minh được \(\widehat {KMA} = \widehat {BMN}\) và \(\widehat {KMA} + \widehat {KMN} + \widehat {BMN} = {180^o} \Rightarrow \widehat {KMN} = {180^o} - 2\widehat {KMA}\).
+ Chứng minh tương tự ta có: \(\widehat {NPQ} = \widehat {PQK} = \widehat {QKM} = {180^o} - 2\widehat {KMA}\). Do đó, đa giác MNPQK là ngũ giác đều.
Lời giải chi tiết:
Vì ABCDE là ngũ giác đều nên \(AB = BC = CD = DE = EA\), \(\widehat A = \widehat B = \widehat C = \widehat D = \widehat E\)
Vì M, N, P, Q, K lần lượt là trung điểm của các cạnh AB, BC, CD, DE, EA.
Do đó, \(AM = MB = NB = NC = CP = PD = DQ = QE = EK = KA\)
Ta có: \(AM = MB = NB = NC = CP = PD = DQ = QE = EK = KA\) và \(\widehat A = \widehat B = \widehat C = \widehat D = \widehat E\)
Suy ra: \(\Delta AMK = \Delta BMN = \Delta CPN = \Delta DPQ = \Delta EKQ\left( {c.g.c} \right)\)
Do đó: + \(KM = MN = PN = PQ = QK\left( 1 \right)\).
+ \(\widehat {KMA} = \widehat {AKM} = \widehat {BMN} = \widehat {MNB} = \widehat {CNP} = \widehat {CPN} = \widehat {DPQ} = \widehat {DQP} = \widehat {EQK} = \widehat {EKQ}\)
Ta có: \(\widehat {KMA} + \widehat {KMN} + \widehat {BMN} = {180^o}\) (các góc kề bù)
Mà \(\widehat {KMA} = \widehat {BMN}\) nên \(\widehat {KMN} = {180^o} - 2\widehat {KMA}\).
Vì \(\widehat {BNM} + \widehat {MNP} + \widehat {PNC} = {180^o}\) (các góc kề bù)
Mà \(\widehat {KMA} = \widehat {BNM} = \widehat {PNC}\) nên \(\widehat {MNP} = {180^o} - 2\widehat {KMA}\).
Chứng minh tương tự ta có:
\(\widehat {NPQ} = \widehat {PQK} = \widehat {QKM} = {180^o} - 2\widehat {KMA}\)
Do đó, \(\widehat {KMN} = \widehat {MNP} = \widehat {NPQ} = \widehat {PQK} = \widehat {QKM}\left( 2 \right)\)
Từ (1) và (2) suy ra: MNPQK là ngũ giác đều.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 1 trang 84 SGK Toán 9 Kết nối tri thức
Ta đã biết các tam giác đều và hình vuông có các đỉnh nằm trên một đường tròn. Ta dựng một đa giác lồi 5 cạnh có các đỉnh nằm trên một đường tròn như sau:
- Vẽ đường tròn tâm O bán kính R.
- Lần lượt lấy các điểm A, B, C, D, E trên đường tròn theo thứ tự ngược chiều kim đồng hồ (hoặc theo chiều kim đồng hồ) sao cho: \(\widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOA} = \frac{{{{360}^o}}}{5} = {72^o}\).
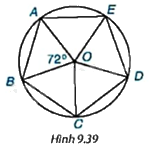
Em hãy giải thích vì sao các cạnh và các góc của đa giác ABCDE bằng nhau (H.9.39).
Phương pháp giải:
+ Chứng minh được các tam giác \(\Delta EOA = \Delta EOD = \Delta COD = \Delta COB = \Delta AOB\left( {c.g.c} \right)\)
Suy ra: \(AE = ED = DC = CB = BA\) và
\(\widehat {OAE} = \widehat {OEA} = \widehat {ODE} = \widehat {OED} = \widehat {ODC} = \widehat {OCD} = \widehat {OCB} = \widehat {OBC} = \widehat {OBA} = \widehat {OAB}\)
+ Suy ra: \(\widehat {BAE} = \widehat {AED} = \widehat {EDC} = \widehat {DCB} = \widehat {CBA}\)
Lời giải chi tiết:
Vì đa giác ABCDE nội tiếp đường tròn (O) nên \(OA = OB = OC = OD = OE\).
Theo giả thiết: \(\widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOA} = {72^o}\)
Do đó, \(\Delta EOA = \Delta EOD = \Delta COD = \Delta COB = \Delta AOB\left( {c.g.c} \right)\).
Suy ra:
+) \(AE = ED = DC = CB = BA\)
+) \(\widehat {OAE} = \widehat {OEA} = \widehat {ODE} = \widehat {OED} = \widehat {ODC} = \widehat {OCD} = \widehat {OCB} = \widehat {OBC} = \widehat {OBA} = \widehat {OAB}\)
Do đó, \(\widehat {OAE} + \widehat {OAB} = \widehat {OEA} + \widehat {OED} = \widehat {ODE} + \widehat {ODC} = \widehat {OCD} + \widehat {OCB} = \widehat {OBC} + \widehat {OBA}\)
Suy ra: \(\widehat {BAE} = \widehat {AED} = \widehat {EDC} = \widehat {DCB} = \widehat {CBA}\).
Vậy các cạnh và các góc của đa giác ABCDE bằng nhau.
Video hướng dẫn giải
Trả lời câu hỏi Thử thách nhỏ 1 trang 87SGK Toán 9 Kết nối tri thức
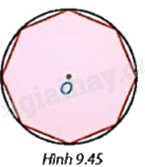
Cho một bát giác đều (đa giác đều 8 cạnh) nội tiếp một đường tròn tâm O (H.9.45). Hỏi mỗi góc của bát giác đều có số đo bằng bao nhiêu?
Phương pháp giải:
+ Gọi ABCDEFGH là bát giác đều nội tiếp đường tròn (O).
+ Chứng minh \(\Delta AOH = \Delta GOH = \Delta GOF = \Delta EOF = \Delta EOD = \Delta COD = \Delta COB = \Delta AOB\left( {c.c.c} \right)\), suy ra: \(\widehat {HOA} = \widehat {HOG} = \widehat {GOF} = \widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOF} = \frac{{{{360}^o}}}{8} = {45^o}\)
+ Tính được: \(\widehat {OAB} = \widehat {OBA} = \frac{{{{180}^o} - \widehat {AOB}}}{2} = 67,{5^o}\)
+ Do đó \(\widehat {ABC} = \widehat {BCD} = \widehat {CDE} = \widehat {DEF} = \widehat {EFG} = \widehat {FGH} = \widehat {GHA} = {135^o}\)
Lời giải chi tiết:
Gọi ABCDEFGH là bát giác đều nội tiếp đường tròn (O).
Vì ABCDEFGH là bát giác đều nên \(AB = BC = CD = DE = EF = FG = GH = HA\).
Vì ABCDEFGH là bát giác đều nội tiếp (O) nên \(OA = OB = OC = OD = OE = OF = OH = OG\).
Do đó, \(\Delta AOH = \Delta GOH = \Delta GOF = \Delta EOF = \Delta EOD = \Delta COD = \Delta COB = \Delta AOB\left( {c.c.c} \right)\)
Suy ra: \(\widehat {HOA} = \widehat {HOG} = \widehat {GOF} = \widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOF} = \frac{{{{360}^o}}}{8} = {45^o}\)
Tam giác AOB cân tại O (do \(OA = OB\)) nên \(\widehat {OAB} = \widehat {OBA}\).Do đó, \(\widehat {OAB} = \widehat {OBA} = \frac{{{{180}^o} - \widehat {AOB}}}{2} = 67,{5^o}\)
Chứng minh tương tự ta có:
\(\widehat {OBC} = \widehat {OCB} = \widehat {ODE} = \widehat {OED} = \widehat {OEF} = \widehat {OFE} = \widehat {OFG} = \widehat {OGF} = \widehat {OGH} = \widehat {OHG} = \widehat {OHA} = \widehat {OAH} = 67,{5^o}\)
Suy ra \(\widehat {ABC} = \widehat {BCD} = \widehat {CDE} = \widehat {DEF} = \widehat {EFG} = \widehat {FGH} = \widehat {GHA} = {135^o}\).
Vậy mỗi góc của bát giác đều bằng \({135^o}\).
Video hướng dẫn giải
Trả lời câu hỏi Câu hỏi trang 85 SGK Toán 9 Kết nối tri thức
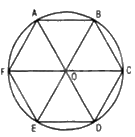
Nếu một lục giác đều (đa giác đều 6 cạnh) nội tiếp một đường tròn bán kính 2cm (H.9.40) thì độ dài các cạnh của lục giác đều đó bằng bao nhiêu centimét? Số đo các góc của lục giác đều bằng bao nhiêu độ?
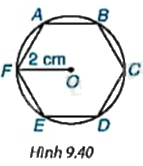
Phương pháp giải:
+ Chứng minh \(\Delta AOF = \Delta EOF = \Delta EOD = \Delta COD = \Delta COB = \Delta AOB\left( {c.c.c} \right)\), suy ra
\(\widehat {FOA} = \widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOF} = \frac{{{{360}^o}}}{6} = {60^o}\)
+ Chứng minh tam giác AOB đều, từ đó tính được AB và \(\widehat {OAB} = \widehat {OBA} = {60^o}\).
+ Tính được \(\widehat {FAB} = \widehat {ABC} = \widehat {BCD} = \widehat {CDE} = \widehat {DEF} = \widehat {EFA} = {120^o}\).
Lời giải chi tiết:
Vì ABCDEF là lục giác đều \(AB = BC = CD = DE = EF = FA\).
Mà lục giác ABCDEF nội tiếp đường tròn (O) nên \(OA = OB = OC = OD = OE = OF\).
Do đó, \(\Delta AOF = \Delta EOF = \Delta EOD = \Delta COD = \Delta COB = \Delta AOB\left( {c.c.c} \right)\)
Do đó,
+) \(\widehat {FOA}\)\( = \widehat {AOB}\)\( = \widehat {BOC}\)\( = \widehat {COD}\)\( = \widehat {DOE}\)\( = \widehat {EOF}\)\( = \frac{{{{360}^o}}}{6}\)\( = {60^o}\)
+) \(\widehat {OAF}\)\( = \widehat {OFA}\)\( = \widehat {OEF}\)\( = \widehat {OFE}\)\( = \widehat {ODE}\)\( = \widehat {OED}\)\( = \widehat {ODC}\)\( = \widehat {OCD}\)\( = \widehat {OCB}\)\( = \widehat {OBC}\)\( = \widehat {OBA}\)\( = \widehat {OAB}\)
Tam giác AOB có: \(OA = OB,\widehat {AOB} = {60^o}\) nên tam giác OAB đều.
Do đó, \(OA = AB = 2cm\) và \(\widehat {OAB} = \widehat {OBA} = {60^o}\)
Suy ra:
\(\widehat {OAF} + \widehat {OAB}\)\( = \widehat {OFA} + \widehat {OFE}\)\( = \widehat {OEF} + \widehat {OED}\)\( = \widehat {ODE} + \widehat {ODC}\)\( = \widehat {OCD} + \widehat {OCB}\)\( = \widehat {OBC} + \widehat {OBA}\)\( = {60^o} + {60^o}\)\( = {120^o}\)
Do đó: \(\widehat {FAB} = \widehat {ABC} = \widehat {BCD} = \widehat {CDE} = \widehat {DEF} = \widehat {EFA} = {120^o}\)
Vậy lục giác đều ABCDEF nội tiếp (O) bán kính 2cm có độ dài cạnh bằng 2cm và số đo các góc lục giác đều bằng \({120^o}\)
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 1 trang 84 SGK Toán 9 Kết nối tri thức
Ta đã biết các tam giác đều và hình vuông có các đỉnh nằm trên một đường tròn. Ta dựng một đa giác lồi 5 cạnh có các đỉnh nằm trên một đường tròn như sau:
- Vẽ đường tròn tâm O bán kính R.
- Lần lượt lấy các điểm A, B, C, D, E trên đường tròn theo thứ tự ngược chiều kim đồng hồ (hoặc theo chiều kim đồng hồ) sao cho: \(\widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOA} = \frac{{{{360}^o}}}{5} = {72^o}\).
Em hãy giải thích vì sao các cạnh và các góc của đa giác ABCDE bằng nhau (H.9.39).
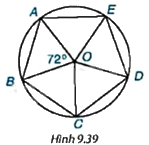
Phương pháp giải:
+ Chứng minh được các tam giác \(\Delta EOA = \Delta EOD = \Delta COD = \Delta COB = \Delta AOB\left( {c.g.c} \right)\)
Suy ra: \(AE = ED = DC = CB = BA\) và
\(\widehat {OAE} = \widehat {OEA} = \widehat {ODE} = \widehat {OED} = \widehat {ODC} = \widehat {OCD} = \widehat {OCB} = \widehat {OBC} = \widehat {OBA} = \widehat {OAB}\)
+ Suy ra: \(\widehat {BAE} = \widehat {AED} = \widehat {EDC} = \widehat {DCB} = \widehat {CBA}\)
Lời giải chi tiết:
Vì đa giác ABCDE nội tiếp đường tròn (O) nên \(OA = OB = OC = OD = OE\).
Theo giả thiết: \(\widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOA} = {72^o}\)
Do đó, \(\Delta EOA = \Delta EOD = \Delta COD = \Delta COB = \Delta AOB\left( {c.g.c} \right)\).
Suy ra:
+) \(AE = ED = DC = CB = BA\)
+) \(\widehat {OAE} = \widehat {OEA} = \widehat {ODE} = \widehat {OED} = \widehat {ODC} = \widehat {OCD} = \widehat {OCB} = \widehat {OBC} = \widehat {OBA} = \widehat {OAB}\)
Do đó, \(\widehat {OAE} + \widehat {OAB} = \widehat {OEA} + \widehat {OED} = \widehat {ODE} + \widehat {ODC} = \widehat {OCD} + \widehat {OCB} = \widehat {OBC} + \widehat {OBA}\)
Suy ra: \(\widehat {BAE} = \widehat {AED} = \widehat {EDC} = \widehat {DCB} = \widehat {CBA}\).
Vậy các cạnh và các góc của đa giác ABCDE bằng nhau.
Video hướng dẫn giải
Trả lời câu hỏi Câu hỏi trang 85 SGK Toán 9 Kết nối tri thức
Nếu một lục giác đều (đa giác đều 6 cạnh) nội tiếp một đường tròn bán kính 2cm (H.9.40) thì độ dài các cạnh của lục giác đều đó bằng bao nhiêu centimét? Số đo các góc của lục giác đều bằng bao nhiêu độ?
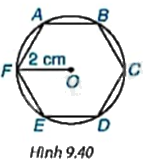
Phương pháp giải:
+ Chứng minh \(\Delta AOF = \Delta EOF = \Delta EOD = \Delta COD = \Delta COB = \Delta AOB\left( {c.c.c} \right)\), suy ra
\(\widehat {FOA} = \widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOF} = \frac{{{{360}^o}}}{6} = {60^o}\)
+ Chứng minh tam giác AOB đều, từ đó tính được AB và \(\widehat {OAB} = \widehat {OBA} = {60^o}\).
+ Tính được \(\widehat {FAB} = \widehat {ABC} = \widehat {BCD} = \widehat {CDE} = \widehat {DEF} = \widehat {EFA} = {120^o}\).
Lời giải chi tiết:
Vì ABCDEF là lục giác đều \(AB = BC = CD = DE = EF = FA\).
Mà lục giác ABCDEF nội tiếp đường tròn (O) nên \(OA = OB = OC = OD = OE = OF\).
Do đó, \(\Delta AOF = \Delta EOF = \Delta EOD = \Delta COD = \Delta COB = \Delta AOB\left( {c.c.c} \right)\)
Do đó,
+) \(\widehat {FOA}\)\( = \widehat {AOB}\)\( = \widehat {BOC}\)\( = \widehat {COD}\)\( = \widehat {DOE}\)\( = \widehat {EOF}\)\( = \frac{{{{360}^o}}}{6}\)\( = {60^o}\)
+) \(\widehat {OAF}\)\( = \widehat {OFA}\)\( = \widehat {OEF}\)\( = \widehat {OFE}\)\( = \widehat {ODE}\)\( = \widehat {OED}\)\( = \widehat {ODC}\)\( = \widehat {OCD}\)\( = \widehat {OCB}\)\( = \widehat {OBC}\)\( = \widehat {OBA}\)\( = \widehat {OAB}\)
Tam giác AOB có: \(OA = OB,\widehat {AOB} = {60^o}\) nên tam giác OAB đều.
Do đó, \(OA = AB = 2cm\) và \(\widehat {OAB} = \widehat {OBA} = {60^o}\)
Suy ra:
\(\widehat {OAF} + \widehat {OAB}\)\( = \widehat {OFA} + \widehat {OFE}\)\( = \widehat {OEF} + \widehat {OED}\)\( = \widehat {ODE} + \widehat {ODC}\)\( = \widehat {OCD} + \widehat {OCB}\)\( = \widehat {OBC} + \widehat {OBA}\)\( = {60^o} + {60^o}\)\( = {120^o}\)
Do đó: \(\widehat {FAB} = \widehat {ABC} = \widehat {BCD} = \widehat {CDE} = \widehat {DEF} = \widehat {EFA} = {120^o}\)
Vậy lục giác đều ABCDEF nội tiếp (O) bán kính 2cm có độ dài cạnh bằng 2cm và số đo các góc lục giác đều bằng \({120^o}\)
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 1 trang 86 SGK Toán 9 Kết nối tri thức
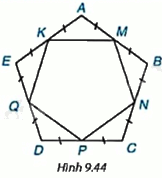
Cho M, N, P, Q, K lần lượt là trung điểm của các cạnh AB, BC, CD, DE và EA của ngũ giác đều ABCDE (H.9.44). Hỏi MNPQK có phải là ngũ giác đều hay không?
Phương pháp giải:
+ Chứng minh \(\Delta AMK = \Delta BMN = \Delta CPN = \Delta DPQ = \Delta EKQ\left( {c.g.c} \right)\) nên \(KM = MN = PN = PQ = QK\).
+ Chứng minh được \(\widehat {KMA} = \widehat {BMN}\) và \(\widehat {KMA} + \widehat {KMN} + \widehat {BMN} = {180^o} \Rightarrow \widehat {KMN} = {180^o} - 2\widehat {KMA}\).
+ Chứng minh tương tự ta có: \(\widehat {NPQ} = \widehat {PQK} = \widehat {QKM} = {180^o} - 2\widehat {KMA}\). Do đó, đa giác MNPQK là ngũ giác đều.
Lời giải chi tiết:
Vì ABCDE là ngũ giác đều nên \(AB = BC = CD = DE = EA\), \(\widehat A = \widehat B = \widehat C = \widehat D = \widehat E\)
Vì M, N, P, Q, K lần lượt là trung điểm của các cạnh AB, BC, CD, DE, EA.
Do đó, \(AM = MB = NB = NC = CP = PD = DQ = QE = EK = KA\)
Ta có: \(AM = MB = NB = NC = CP = PD = DQ = QE = EK = KA\) và \(\widehat A = \widehat B = \widehat C = \widehat D = \widehat E\)
Suy ra: \(\Delta AMK = \Delta BMN = \Delta CPN = \Delta DPQ = \Delta EKQ\left( {c.g.c} \right)\)
Do đó: + \(KM = MN = PN = PQ = QK\left( 1 \right)\).
+ \(\widehat {KMA} = \widehat {AKM} = \widehat {BMN} = \widehat {MNB} = \widehat {CNP} = \widehat {CPN} = \widehat {DPQ} = \widehat {DQP} = \widehat {EQK} = \widehat {EKQ}\)
Ta có: \(\widehat {KMA} + \widehat {KMN} + \widehat {BMN} = {180^o}\) (các góc kề bù)
Mà \(\widehat {KMA} = \widehat {BMN}\) nên \(\widehat {KMN} = {180^o} - 2\widehat {KMA}\).
Vì \(\widehat {BNM} + \widehat {MNP} + \widehat {PNC} = {180^o}\) (các góc kề bù)
Mà \(\widehat {KMA} = \widehat {BNM} = \widehat {PNC}\) nên \(\widehat {MNP} = {180^o} - 2\widehat {KMA}\).
Chứng minh tương tự ta có:
\(\widehat {NPQ} = \widehat {PQK} = \widehat {QKM} = {180^o} - 2\widehat {KMA}\)
Do đó, \(\widehat {KMN} = \widehat {MNP} = \widehat {NPQ} = \widehat {PQK} = \widehat {QKM}\left( 2 \right)\)
Từ (1) và (2) suy ra: MNPQK là ngũ giác đều.
Video hướng dẫn giải
Trả lời câu hỏi Thử thách nhỏ 1 trang 87SGK Toán 9 Kết nối tri thức
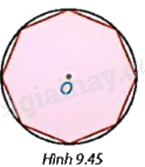
Cho một bát giác đều (đa giác đều 8 cạnh) nội tiếp một đường tròn tâm O (H.9.45). Hỏi mỗi góc của bát giác đều có số đo bằng bao nhiêu?
Phương pháp giải:
+ Gọi ABCDEFGH là bát giác đều nội tiếp đường tròn (O).
+ Chứng minh \(\Delta AOH = \Delta GOH = \Delta GOF = \Delta EOF = \Delta EOD = \Delta COD = \Delta COB = \Delta AOB\left( {c.c.c} \right)\), suy ra: \(\widehat {HOA} = \widehat {HOG} = \widehat {GOF} = \widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOF} = \frac{{{{360}^o}}}{8} = {45^o}\)
+ Tính được: \(\widehat {OAB} = \widehat {OBA} = \frac{{{{180}^o} - \widehat {AOB}}}{2} = 67,{5^o}\)
+ Do đó \(\widehat {ABC} = \widehat {BCD} = \widehat {CDE} = \widehat {DEF} = \widehat {EFG} = \widehat {FGH} = \widehat {GHA} = {135^o}\)
Lời giải chi tiết:
Gọi ABCDEFGH là bát giác đều nội tiếp đường tròn (O).
Vì ABCDEFGH là bát giác đều nên \(AB = BC = CD = DE = EF = FG = GH = HA\).
Vì ABCDEFGH là bát giác đều nội tiếp (O) nên \(OA = OB = OC = OD = OE = OF = OH = OG\).
Do đó, \(\Delta AOH = \Delta GOH = \Delta GOF = \Delta EOF = \Delta EOD = \Delta COD = \Delta COB = \Delta AOB\left( {c.c.c} \right)\)
Suy ra: \(\widehat {HOA} = \widehat {HOG} = \widehat {GOF} = \widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOF} = \frac{{{{360}^o}}}{8} = {45^o}\)
Tam giác AOB cân tại O (do \(OA = OB\)) nên \(\widehat {OAB} = \widehat {OBA}\).Do đó, \(\widehat {OAB} = \widehat {OBA} = \frac{{{{180}^o} - \widehat {AOB}}}{2} = 67,{5^o}\)
Chứng minh tương tự ta có:
\(\widehat {OBC} = \widehat {OCB} = \widehat {ODE} = \widehat {OED} = \widehat {OEF} = \widehat {OFE} = \widehat {OFG} = \widehat {OGF} = \widehat {OGH} = \widehat {OHG} = \widehat {OHA} = \widehat {OAH} = 67,{5^o}\)
Suy ra \(\widehat {ABC} = \widehat {BCD} = \widehat {CDE} = \widehat {DEF} = \widehat {EFG} = \widehat {FGH} = \widehat {GHA} = {135^o}\).
Vậy mỗi góc của bát giác đều bằng \({135^o}\).
Mục 1 của chương trình Toán 9 tập 2 - Kết nối tri thức thường tập trung vào một chủ đề cụ thể, ví dụ như hàm số bậc hai, hệ phương trình bậc hai, hoặc các ứng dụng của phương trình bậc hai. Việc nắm vững kiến thức nền tảng và kỹ năng giải bài tập trong mục này là rất quan trọng để chuẩn bị cho các bài học tiếp theo và các kỳ thi quan trọng.
Để giúp các em hiểu rõ hơn về nội dung và phương pháp giải các bài tập trong mục 1 trang 84, 85, 86 SGK Toán 9 tập 2 - Kết nối tri thức, chúng ta sẽ đi vào phân tích chi tiết từng bài tập:
Bài tập này thường yêu cầu học sinh vận dụng kiến thức về định nghĩa hàm số bậc hai để xác định các hệ số a, b, c của hàm số. Ngoài ra, bài tập có thể yêu cầu học sinh vẽ đồ thị của hàm số hoặc tìm các điểm đặc biệt trên đồ thị như đỉnh, trục đối xứng, giao điểm với các trục tọa độ.
Bài tập này thường liên quan đến việc tìm tập xác định của hàm số, xét tính đồng biến, nghịch biến của hàm số, hoặc tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số. Để giải bài tập này, học sinh cần nắm vững các khái niệm về tập xác định, tính đơn điệu và cực trị của hàm số.
Bài tập này thường yêu cầu học sinh giải các bài toán thực tế liên quan đến hàm số bậc hai, ví dụ như bài toán tìm quỹ đạo của một vật thể chuyển động, bài toán tối ưu hóa lợi nhuận, hoặc bài toán thiết kế hình học. Để giải bài tập này, học sinh cần biết cách chuyển đổi bài toán thực tế thành bài toán toán học và sử dụng các công cụ của hàm số bậc hai để giải quyết.
Để giải các bài tập trong mục 1 trang 84, 85, 86 SGK Toán 9 tập 2 - Kết nối tri thức một cách hiệu quả, các em có thể áp dụng các phương pháp sau:
Toán 9 là một môn học quan trọng, đòi hỏi sự chăm chỉ và kiên trì. Để học tốt môn Toán 9, các em nên:
Hy vọng rằng với lời giải chi tiết và các phương pháp giải bài tập hiệu quả mà chúng tôi đã cung cấp, các em sẽ tự tin hơn khi giải các bài tập trong mục 1 trang 84, 85, 86 SGK Toán 9 tập 2 - Kết nối tri thức. Chúc các em học tốt và đạt kết quả cao trong học tập!