Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tập 1 của giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong SGK Toán 9 tập 1 Kết nối tri thức, giúp các em nắm vững kiến thức và tự tin hơn trong học tập.
Trang 114, 115, 116 tập trung vào các chủ đề quan trọng của chương học. Hãy cùng chúng tôi khám phá và chinh phục những bài toán này nhé!
Tính toán lượng chất tan và dung môi để pha chế dung dịch có nồng độ phần trăm cho trước Ta cần tính số gam đường cát và số gam nước tinh khiết cần thiết để tạo ra n = 1000 (ml) dung dịch có nồng độ a%. Biết rằng khối lượng riêng của đường cát là d = 1,1 (g/ml) và 1 lít nước tinh khiết nặng 1kg. a) Gọi x (gam) và y (gam) lần lượt là lượng đường cát và nước cất cần pha chế. Lập biểu thức tính thể tích và nồng độ dung dịch để chứng minh x, y thỏa mãn hệ phương trình (left{ begin{array}{l}f
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 1 trang 114 SGK Toán 9 Kết nối tri thức
Tính toán lượng chất tan và dung môi để pha chế dung dịch có nồng độ phần trăm cho trước
Ta cần tính số gam đường cát và số gam nước tinh khiết cần thiết để tạo ra n = 1000 (ml) dung dịch có nồng độ a%. Biết rằng khối lượng riêng của đường cát là d = 1,1 (g/ml) và 1 lít nước tinh khiết nặng 1kg.
a) Gọi x (gam) và y (gam) lần lượt là lượng đường cát và nước cất cần pha chế. Lập biểu thức tính thể tích và nồng độ dung dịch để chứng minh x, y thỏa mãn hệ phương trình
\(\left\{ \begin{array}{l}\frac{x}{{1,1}} + y = 1000\\\frac{x}{{x + y}}.100 = a\end{array} \right.\)
b) Biến đổi hệ phương trình trên về dạng hệ hai phương trình bậc nhất hai ẩn
\(\left\{ \begin{array}{l}x + 1,1y = 1100\\\left( {100 - a} \right)x - ay = 0\end{array} \right.\)
Từ đó chứng tỏ \(\left( {x;y} \right)\) của hệ phương trình này là
\(\left\{ \begin{array}{l}x = \frac{{1100a}}{{110 - 0,1a}}\\y = \frac{{1100\left( {100 - a} \right)}}{{110 - 0,1a}}\end{array} \right.\)
c) Áp dụng: Tính lượng nước và đường cát tương ứng để pha n = 1000 ml nước đường với nồng độ là a = 63%.
Phương pháp giải:
Nồng độ phần trăm C của một dung dịch tính bằng công thức
\(C\% = \frac{{{m_{ct}}}}{{{m_{{\rm{dd}}}}}} \times 100\% \)
Trong đó:
\({m_{ct}}\) là khối lượng chất tan; \({m_{dd}}\) là khối lượng dung dịch
Tính thể tích của một chất = khối lượng của chất đó : khối lượng riêng
Lời giải chi tiết:
Gọi x (gam) và y (gam) lần lượt là lượng đường cát và nước cất cần pha chế
Thể tích của x gam đường cát là \(\frac{x}{{1,1}}\) (ml)
Thể tích của y gam nước cất là y (ml)
Thể tích của dung dịch gồm x gam đường cát và y gam nước cất là \(\frac{x}{{1,1}} + y = 1000\left( 1 \right)\) (ml)
Khối lượng dung dịch là \(x + y\) (gam)
Dung dịch có nồng độ a% nên ta có: \(\frac{x}{{x + y}}.100 = a\left( 2 \right)\)
Từ (1) và (2) ta có x và y là nghiệm của hệ
\(\left\{ \begin{array}{l}\frac{x}{{1,1}} + y = 1000\\\frac{x}{{x + y}}.100 = a\end{array} \right.\)
b) Nhân cả hai vế của phương trình (1) với 1,1 ta được \(x + 1,1y = 1100\left( 3 \right)\)
Từ (2) ta có \(\frac{{100x}}{{x + y}} = a\) hay \(100x = a\left( {x + y} \right)\) nên \(x\left( {100 - a} \right) - ay = 0\left( 4 \right)\)
Từ (3) và (4) nên ta có hệ phương trình
\(\left\{ \begin{array}{l}x + 1,1y = 1100\\\left( {100 - a} \right)x - ay = 0\end{array} \right.\)
Từ phương trình (3) ta có \(x = 1100 - 1,1y\) thay vào phương trình (4) ta được \(\left( {100 - a} \right)\left( {1100 - 1,1y} \right) - ay = 0\) hay \(1100\left( {100 - a} \right) - 1,1y\left( {100 - a} \right) - ay = 0\) suy ra \(y\left( {1,1.\left( {100 - a} \right) + a} \right) = 1100\left( {100 - a} \right)\) nên \(y\left( {110 - 0,1a} \right) = 1100\left( {100 - a} \right)\) do đó \(y = \frac{{1100\left( {100 - a} \right)}}{{110 - 0,1a}}\)
Mà \(x = 1100 - 1,1y = 1100 - 1,1.\frac{{1100\left( {100 - a} \right)}}{{110 - 0,1a}} = 1100 - \frac{{1210\left( {100 - a} \right)}}{{110 - 0,1a}}\)
\( = \frac{{121000 - 110a - 121000 + 1210a}}{{110 - 0,1a}} = \frac{{1100a}}{{110 - 0,1a}}\)
Nên \(\left( {x;y} \right)\) của hệ phương trình này là
\(\left\{ \begin{array}{l}x = \frac{{1100a}}{{110 - 0,1a}}\\y = \frac{{1100\left( {100 - a} \right)}}{{110 - 0,1a}}\end{array} \right.\)
c) Với a = 63% ta có
\(\left\{ \begin{array}{l}x = \frac{{1100.63}}{{110 - 0,1.63}}\\y = \frac{{1100\left( {100 - 63} \right)}}{{110 - 0,1.63}}\end{array} \right.\) hay \(\left\{ \begin{array}{l}x \approx 668,3\\y \approx 392,5\end{array} \right.\)
Vậy cần khoảng 668,3 gam đường cát và 392,5 gam nước cất.
Video hướng dẫn giải
Trả lời câu hỏi Thực hành trang 117 SGK Toán 9 Kết nối tri thức
Tính số gam muối tính khiết và số gam nước tinh khiết cần thiết để có thể pha chế được 1 000 ml dung dịch nước muối sinh lí 0,9%, biết rằng khối lượng riêng của muối tinh khiết là 2,16 g/ml.
Phương pháp giải:
Nồng độ phần trăm C của một dung dịch tính bằng công thức
\(C\% = \frac{{{m_{ct}}}}{{{m_{{\rm{dd}}}}}} \times 100\% \)
Trong đó:
\({m_{ct}}\) là khối lượng chất tan; \({m_{dd}}\) là khối lượng dung dịch
Tính thể tích của một chất = khối lượng của chất đó : khối lượng riêng
Lời giải chi tiết:
Gọi số gam muối tinh khiết là x
Số gam nước tinh khiết là y
Nồng độ muối là 0,9% nên ta có \(\frac{x}{{x + y}}.100 = 0,9\) hay \(100x - 0,9x - 0,9y = 0\) suy ra \(99,1x - 0,9y = 0\left( 1 \right)\)
Thể tích của muối là \(\frac{x}{{2,16}}\) (ml)
Thể tích của nước là y ml nên thể tích của dung dịch là \(\frac{x}{{2,16}} + y = 1000\left( 2 \right)\)
Từ (1) và (2) ta có hệ phương trình
\(\left\{ \begin{array}{l}99,1x - 0,9y = 0\\\frac{x}{{2,16}} + y = 1000\end{array} \right.\)
Giải hệ ta được
\(\left\{ \begin{array}{l}x \approx 9\\y \approx 995,8\end{array} \right.\)
Vậy cần khoảng 9 gam muối tinh khiết và 995,8 gam nước tinh khiết
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 115 SGK Toán 9 Kết nối tri thức
Xây dựng theo các bước sau để xây dựng bảng tính Excel tính toán lượng chất tan và dung môi cần thiết.
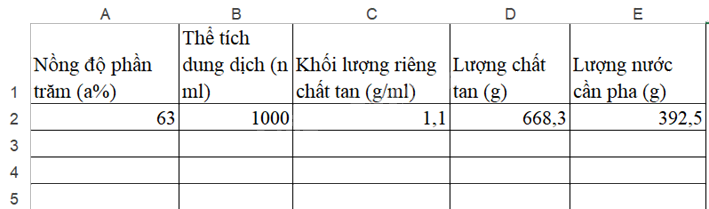
Bước 1: Tạo bảng trên phần mềm Excel, điền các ô thông tin vào bảng tính.

Bước 2: Nhập số liệu vào cột nồng độ phần trăm, thể tích dung dịch, khối lượng riêng của đường (1,1 g/ml).
Bước 3: Sử dụng công thức nghiệm ở HĐ 1 để nhập công thức vào cột chất tan và lượng nước cần pha.
Bước 4: Hoàn thiện bảng tính: Làm tròn số liệu sau dấu phẩy một chữ số và thêm dấu phân cách hàng nghìn cho thể tích dung dịch và khối lượng. Đóng khung cho bảng
Phương pháp giải:
Sử dụng excel trên máy tính để tạo bảng rồi điền số liệu tương ứng.
Lời giải chi tiết:
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 1 trang 114 SGK Toán 9 Kết nối tri thức
Tính toán lượng chất tan và dung môi để pha chế dung dịch có nồng độ phần trăm cho trước
Ta cần tính số gam đường cát và số gam nước tinh khiết cần thiết để tạo ra n = 1000 (ml) dung dịch có nồng độ a%. Biết rằng khối lượng riêng của đường cát là d = 1,1 (g/ml) và 1 lít nước tinh khiết nặng 1kg.
a) Gọi x (gam) và y (gam) lần lượt là lượng đường cát và nước cất cần pha chế. Lập biểu thức tính thể tích và nồng độ dung dịch để chứng minh x, y thỏa mãn hệ phương trình
\(\left\{ \begin{array}{l}\frac{x}{{1,1}} + y = 1000\\\frac{x}{{x + y}}.100 = a\end{array} \right.\)
b) Biến đổi hệ phương trình trên về dạng hệ hai phương trình bậc nhất hai ẩn
\(\left\{ \begin{array}{l}x + 1,1y = 1100\\\left( {100 - a} \right)x - ay = 0\end{array} \right.\)
Từ đó chứng tỏ \(\left( {x;y} \right)\) của hệ phương trình này là
\(\left\{ \begin{array}{l}x = \frac{{1100a}}{{110 - 0,1a}}\\y = \frac{{1100\left( {100 - a} \right)}}{{110 - 0,1a}}\end{array} \right.\)
c) Áp dụng: Tính lượng nước và đường cát tương ứng để pha n = 1000 ml nước đường với nồng độ là a = 63%.
Phương pháp giải:
Nồng độ phần trăm C của một dung dịch tính bằng công thức
\(C\% = \frac{{{m_{ct}}}}{{{m_{{\rm{dd}}}}}} \times 100\% \)
Trong đó:
\({m_{ct}}\) là khối lượng chất tan; \({m_{dd}}\) là khối lượng dung dịch
Tính thể tích của một chất = khối lượng của chất đó : khối lượng riêng
Lời giải chi tiết:
Gọi x (gam) và y (gam) lần lượt là lượng đường cát và nước cất cần pha chế
Thể tích của x gam đường cát là \(\frac{x}{{1,1}}\) (ml)
Thể tích của y gam nước cất là y (ml)
Thể tích của dung dịch gồm x gam đường cát và y gam nước cất là \(\frac{x}{{1,1}} + y = 1000\left( 1 \right)\) (ml)
Khối lượng dung dịch là \(x + y\) (gam)
Dung dịch có nồng độ a% nên ta có: \(\frac{x}{{x + y}}.100 = a\left( 2 \right)\)
Từ (1) và (2) ta có x và y là nghiệm của hệ
\(\left\{ \begin{array}{l}\frac{x}{{1,1}} + y = 1000\\\frac{x}{{x + y}}.100 = a\end{array} \right.\)
b) Nhân cả hai vế của phương trình (1) với 1,1 ta được \(x + 1,1y = 1100\left( 3 \right)\)
Từ (2) ta có \(\frac{{100x}}{{x + y}} = a\) hay \(100x = a\left( {x + y} \right)\) nên \(x\left( {100 - a} \right) - ay = 0\left( 4 \right)\)
Từ (3) và (4) nên ta có hệ phương trình
\(\left\{ \begin{array}{l}x + 1,1y = 1100\\\left( {100 - a} \right)x - ay = 0\end{array} \right.\)
Từ phương trình (3) ta có \(x = 1100 - 1,1y\) thay vào phương trình (4) ta được \(\left( {100 - a} \right)\left( {1100 - 1,1y} \right) - ay = 0\) hay \(1100\left( {100 - a} \right) - 1,1y\left( {100 - a} \right) - ay = 0\) suy ra \(y\left( {1,1.\left( {100 - a} \right) + a} \right) = 1100\left( {100 - a} \right)\) nên \(y\left( {110 - 0,1a} \right) = 1100\left( {100 - a} \right)\) do đó \(y = \frac{{1100\left( {100 - a} \right)}}{{110 - 0,1a}}\)
Mà \(x = 1100 - 1,1y = 1100 - 1,1.\frac{{1100\left( {100 - a} \right)}}{{110 - 0,1a}} = 1100 - \frac{{1210\left( {100 - a} \right)}}{{110 - 0,1a}}\)
\( = \frac{{121000 - 110a - 121000 + 1210a}}{{110 - 0,1a}} = \frac{{1100a}}{{110 - 0,1a}}\)
Nên \(\left( {x;y} \right)\) của hệ phương trình này là
\(\left\{ \begin{array}{l}x = \frac{{1100a}}{{110 - 0,1a}}\\y = \frac{{1100\left( {100 - a} \right)}}{{110 - 0,1a}}\end{array} \right.\)
c) Với a = 63% ta có
\(\left\{ \begin{array}{l}x = \frac{{1100.63}}{{110 - 0,1.63}}\\y = \frac{{1100\left( {100 - 63} \right)}}{{110 - 0,1.63}}\end{array} \right.\) hay \(\left\{ \begin{array}{l}x \approx 668,3\\y \approx 392,5\end{array} \right.\)
Vậy cần khoảng 668,3 gam đường cát và 392,5 gam nước cất.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 115 SGK Toán 9 Kết nối tri thức
Xây dựng theo các bước sau để xây dựng bảng tính Excel tính toán lượng chất tan và dung môi cần thiết.
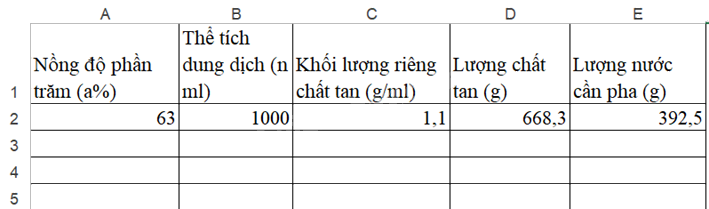
Bước 1: Tạo bảng trên phần mềm Excel, điền các ô thông tin vào bảng tính.

Bước 2: Nhập số liệu vào cột nồng độ phần trăm, thể tích dung dịch, khối lượng riêng của đường (1,1 g/ml).
Bước 3: Sử dụng công thức nghiệm ở HĐ 1 để nhập công thức vào cột chất tan và lượng nước cần pha.
Bước 4: Hoàn thiện bảng tính: Làm tròn số liệu sau dấu phẩy một chữ số và thêm dấu phân cách hàng nghìn cho thể tích dung dịch và khối lượng. Đóng khung cho bảng
Phương pháp giải:
Sử dụng excel trên máy tính để tạo bảng rồi điền số liệu tương ứng.
Lời giải chi tiết:
Video hướng dẫn giải
Trả lời câu hỏi Thực hành trang 117 SGK Toán 9 Kết nối tri thức
Tính số gam muối tính khiết và số gam nước tinh khiết cần thiết để có thể pha chế được 1 000 ml dung dịch nước muối sinh lí 0,9%, biết rằng khối lượng riêng của muối tinh khiết là 2,16 g/ml.
Phương pháp giải:
Nồng độ phần trăm C của một dung dịch tính bằng công thức
\(C\% = \frac{{{m_{ct}}}}{{{m_{{\rm{dd}}}}}} \times 100\% \)
Trong đó:
\({m_{ct}}\) là khối lượng chất tan; \({m_{dd}}\) là khối lượng dung dịch
Tính thể tích của một chất = khối lượng của chất đó : khối lượng riêng
Lời giải chi tiết:
Gọi số gam muối tinh khiết là x
Số gam nước tinh khiết là y
Nồng độ muối là 0,9% nên ta có \(\frac{x}{{x + y}}.100 = 0,9\) hay \(100x - 0,9x - 0,9y = 0\) suy ra \(99,1x - 0,9y = 0\left( 1 \right)\)
Thể tích của muối là \(\frac{x}{{2,16}}\) (ml)
Thể tích của nước là y ml nên thể tích của dung dịch là \(\frac{x}{{2,16}} + y = 1000\left( 2 \right)\)
Từ (1) và (2) ta có hệ phương trình
\(\left\{ \begin{array}{l}99,1x - 0,9y = 0\\\frac{x}{{2,16}} + y = 1000\end{array} \right.\)
Giải hệ ta được
\(\left\{ \begin{array}{l}x \approx 9\\y \approx 995,8\end{array} \right.\)
Vậy cần khoảng 9 gam muối tinh khiết và 995,8 gam nước tinh khiết
Chương 3 của SGK Toán 9 tập 1 Kết nối tri thức tập trung vào chủ đề Hệ hai phương trình tuyến tính. Các bài tập trang 114, 115, 116 xoay quanh việc giải hệ phương trình bằng phương pháp thế và phương pháp cộng đại số, cũng như ứng dụng của hệ phương trình vào giải bài toán thực tế.
Trước khi đi vào giải chi tiết các bài tập, chúng ta cùng ôn lại hai phương pháp giải hệ phương trình tuyến tính phổ biến nhất:
Bài 1: Giải các hệ phương trình sau bằng phương pháp thế:
a) { x + y = 5 2x - y = 1
b) { 3x - 2y = 7 x + y = 1
Lời giải:
a) Từ phương trình x + y = 5, ta có y = 5 - x. Thay vào phương trình 2x - y = 1, ta được 2x - (5 - x) = 1, suy ra 3x = 6, x = 2. Thay x = 2 vào y = 5 - x, ta được y = 3. Vậy nghiệm của hệ phương trình là (x; y) = (2; 3).
b) Từ phương trình x + y = 1, ta có x = 1 - y. Thay vào phương trình 3x - 2y = 7, ta được 3(1 - y) - 2y = 7, suy ra 3 - 3y - 2y = 7, -5y = 4, y = -4/5. Thay y = -4/5 vào x = 1 - y, ta được x = 9/5. Vậy nghiệm của hệ phương trình là (x; y) = (9/5; -4/5).
Bài 2: Giải các hệ phương trình sau bằng phương pháp cộng đại số:
a) { 2x + y = 7 x - y = 2
b) { x + 2y = 5 2x - y = 3
Lời giải:
a) Cộng hai phương trình lại, ta được 3x = 9, x = 3. Thay x = 3 vào phương trình x - y = 2, ta được 3 - y = 2, y = 1. Vậy nghiệm của hệ phương trình là (x; y) = (3; 1).
b) Nhân phương trình thứ hai với 2, ta được 4x - 2y = 6. Cộng phương trình này với phương trình x + 2y = 5, ta được 5x = 11, x = 11/5. Thay x = 11/5 vào phương trình x + 2y = 5, ta được 11/5 + 2y = 5, 2y = 14/5, y = 7/5. Vậy nghiệm của hệ phương trình là (x; y) = (11/5; 7/5).
Bài 3: Một người đi xe máy từ A đến B với vận tốc 40 km/h. Sau khi đi được 30 phút, người đó tăng vận tốc lên 50 km/h và đến B muộn hơn 10 phút so với dự kiến. Tính quãng đường AB.
Lời giải:
Gọi x là quãng đường AB (km). Thời gian dự kiến đi từ A đến B là x/40 (giờ). Thời gian thực tế đi từ A đến B là 30 phút (0.5 giờ) với vận tốc 40 km/h, sau đó đi quãng đường còn lại (x - 20) km với vận tốc 50 km/h. Thời gian thực tế là 0.5 + (x - 20)/50 (giờ). Theo đề bài, thời gian thực tế muộn hơn dự kiến 10 phút (1/6 giờ), nên ta có phương trình: 0.5 + (x - 20)/50 = x/40 + 1/6. Giải phương trình này, ta được x = 100. Vậy quãng đường AB là 100 km.
Hy vọng với lời giải chi tiết này, các em sẽ hiểu rõ hơn về cách giải các bài tập hệ phương trình tuyến tính và ứng dụng của chúng. Chúc các em học tập tốt!