Bài tập 4.29 trang 82 SGK Toán 9 tập 1 thuộc chương Hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế. Giaitoan.edu.vn sẽ cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác, cập nhật và hữu ích nhất cho học sinh. Hãy cùng giaitoan.edu.vn khám phá lời giải bài tập 4.29 này nhé!
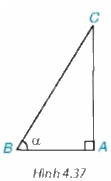
Cho tam giác ABC vuông tại A, có (widehat B = alpha ) (H.4.37). a) Hãy viết các tỉ số lượng giác (sin alpha ;cos alpha ) b) Sử dụng định lý Pythagore, chứng minh rằng ({sin ^2}alpha + {cos ^2}alpha = 1)
Đề bài
Cho tam giác ABC vuông tại A, có \(\widehat B = \alpha \) (H.4.37).
a) Hãy viết các tỉ số lượng giác \(\sin \alpha ;\cos \alpha \)
b) Sử dụng định lý Pythagore, chứng minh rằng \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Tỉ số giữa cạnh đối và cạnh huyền là \(\sin \alpha \)
Tỉ số giữa cạnh kề với cạnh huyền là \(\cos \alpha \)
Định lý Pythagore: cạnh huyền bình phương bằng tổng bình phương của hai cạnh góc vuông.
Lời giải chi tiết
a) Ta có \(\sin \alpha = \frac{{AC}}{{BC}};\cos \alpha = \frac{{AB}}{{BC}}\)
b) Tam giác ABC vuông tại A nên ta có: \(A{B^2} + A{C^2} = B{C^2}\) (định lý Pythagore)
Nên ta có
\({\sin ^2}\alpha + {\cos ^2}\alpha = {\left( {\frac{{AC}}{{BC}}} \right)^2} + {\left( {\frac{{AB}}{{BC}}} \right)^2} = \frac{{A{C^2} + A{B^2}}}{{B{C^2}}} = \frac{{B{C^2}}}{{B{C^2}}} = 1\) (đpcm).
Bài tập 4.29 trang 82 SGK Toán 9 tập 1 - Kết nối tri thức là một bài toán ứng dụng thực tế về hàm số bậc nhất. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về hàm số bậc nhất, bao gồm:
(Đề bài sẽ được chèn vào đây - ví dụ: Một người đi xe máy từ A đến B với vận tốc 40km/h. Hỏi người đó đi hết bao lâu nếu quãng đường AB dài 120km?)
Để giải bài tập này, ta có thể sử dụng công thức tính thời gian: Thời gian = Quãng đường / Vận tốc
Trong bài toán này:
Vậy thời gian người đó đi hết là: 120km / 40km/h = 3 giờ
Kết luận: Người đó đi hết 3 giờ để đi từ A đến B.
Bài toán này là một ví dụ điển hình về ứng dụng của hàm số bậc nhất trong việc mô tả mối quan hệ giữa quãng đường, vận tốc và thời gian. Nếu ta coi quãng đường là biến y, vận tốc là hệ số a và thời gian là biến x, thì ta có hàm số y = ax. Trong trường hợp này, a = 40km/h, và y là quãng đường đi được sau x giờ.
Ngoài bài tập 4.29, còn rất nhiều bài tập tương tự về ứng dụng hàm số bậc nhất trong thực tế. Để giải các bài tập này, học sinh cần:
Hàm số bậc nhất là một trong những khái niệm quan trọng trong chương trình Toán 9. Việc nắm vững kiến thức về hàm số bậc nhất sẽ giúp học sinh giải quyết nhiều bài toán khác nhau, không chỉ trong môn Toán mà còn trong các môn học khác. Để hiểu sâu hơn về hàm số bậc nhất, học sinh có thể tham khảo thêm các tài liệu sau:
Để củng cố kiến thức về hàm số bậc nhất và rèn luyện kỹ năng giải bài tập, học sinh nên tự giải thêm các bài tập khác trong SGK và sách bài tập Toán 9 tập 1 - Kết nối tri thức. Ngoài ra, học sinh cũng có thể tìm kiếm các bài tập tương tự trên mạng hoặc nhờ thầy cô giáo hướng dẫn.
Bài tập 4.29 trang 82 SGK Toán 9 tập 1 - Kết nối tri thức là một bài toán ứng dụng thực tế về hàm số bậc nhất. Hy vọng rằng với lời giải chi tiết và phân tích sâu sắc mà giaitoan.edu.vn cung cấp, các em học sinh đã hiểu rõ phương pháp giải bài tập này và tự tin làm bài tập. Chúc các em học tập tốt!