Chào mừng bạn đến với bài học về lý thuyết bất phương trình bậc nhất một ẩn trong chương trình Toán 9 Kết nối tri thức. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về bất phương trình, giúp bạn tự tin giải quyết các bài toán liên quan.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, các tính chất, quy tắc biến đổi bất phương trình và cách giải bất phương trình bậc nhất một ẩn một cách chi tiết và dễ hiểu.
1. Khái niệm bất phương trình bậc nhất một ẩn Khái niệm bất phương trình bậc nhất một ẩn
1. Khái niệm bất phương trình bậc nhất một ẩn
Khái niệm bất phương trình bậc nhất một ẩn
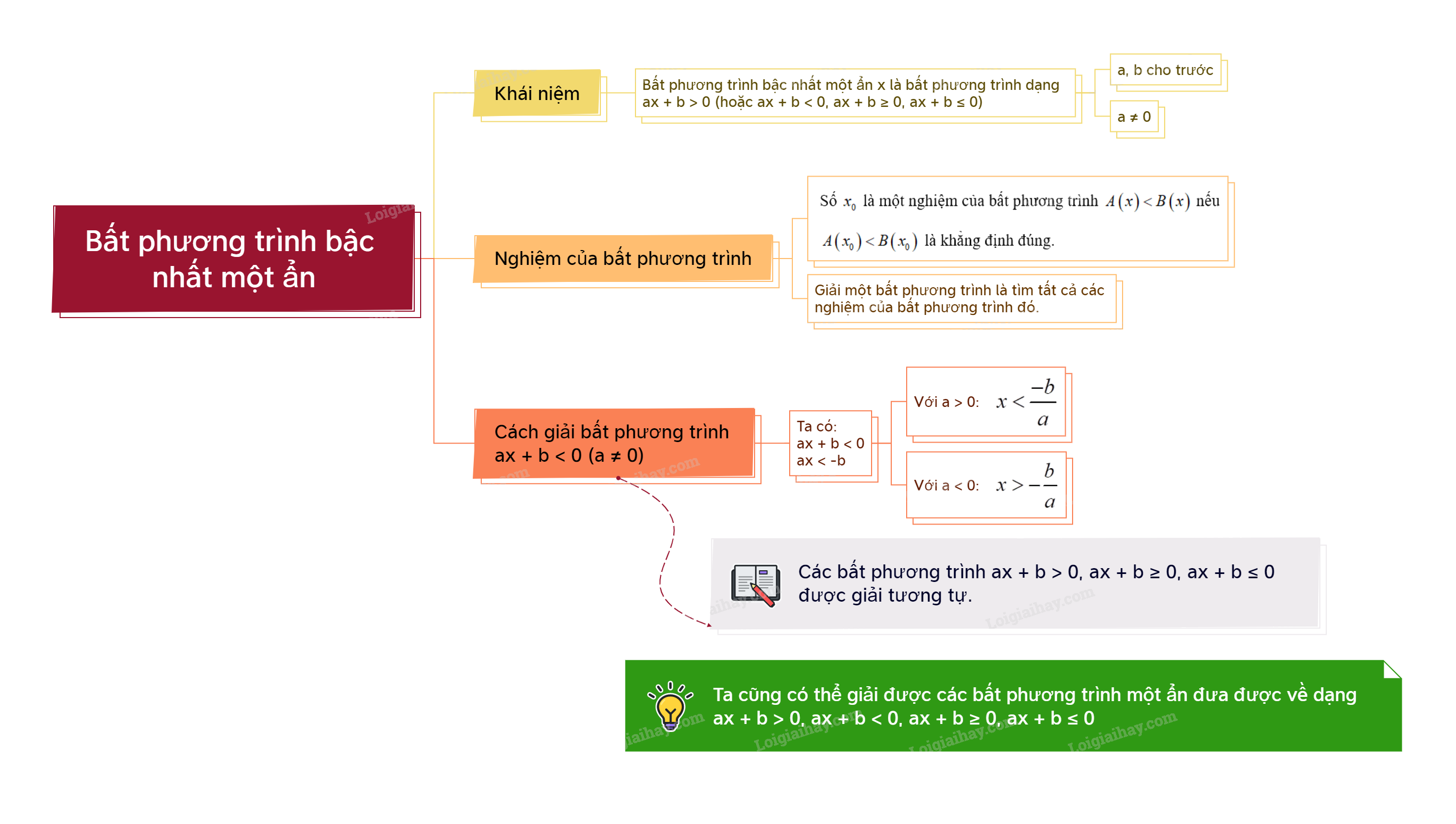
Bất phương trình dạng \(ax + b < 0\) (hoặc \(ax + b > 0\); \(ax + b \le 0\); \(ax + b \ge 0\)) trong đó a, b là hai số đã cho, \(a \ne 0\) được gọi là bất phương trình bậc nhất một ẩn x. |
Ví dụ: \(3x + 16 \le 0\); \( - 3x > 0\) là các bất phương trình bậc nhất một ẩn x.
\({x^2} - 4 \ge 0\) không phải là một bất phương trình bậc nhất một ẩn x vì \({x^2} - 4\) là một đa thức bậc hai.
\(3x - 2y < 2\) không phải là một bất phương trình bậc nhất một ẩn vì đa thức \(3x - 2y\) là đa thức với hai biến x và y.
Nghiệm của bất phương trình
- Số \({x_0}\) là một nghiệm của bất phương trình \(A\left( x \right) < B\left( x \right)\) nếu \(A\left( {{x_0}} \right) < B\left( {{x_0}} \right)\) là khẳng định đúng. - Giải một bất phương trình là tìm tất cả các nghiệm của bất phương trình đó. |
Ví dụ:
Số -2 là nghiệm của bất phương trình \(2x - 10 < 0\) vì \(2.\left( { - 2} \right) - 10 = - 4 - 10 = - 14 < 0\).
Số 6 không là nghiệm của bất phương trình \(2x - 10 < 0\) vì \(2.6 - 10 = 12 - 10 = 2 > 0\).
2. Cách giải bất phương trình bậc nhất một ẩn
Bất phương trình bậc nhất một ẩn \(ax + b < 0\left( {a \ne 0} \right)\) được giải như sau: \(\begin{array}{l}ax + b < 0\\ax < - b\end{array}\) - Nếu \(a > 0\) thì \(x < \frac{{ - b}}{a}\). - Nếu \(a < 0\) thì \(x > - \frac{b}{a}\). |
Chú ý: Các bất phương trình \(ax + b > 0\), \(ax + b \le 0\), \(ax + b \ge 0\) được giải tương tự.
Ví dụ:Giải bất phương trình \( - 2x - 4 > 0\)
Lời giải:Ta có:
\(\begin{array}{l} - 2x - 4 > 0\\ - 2x > 0 + 4\\ - 2x > 4\\x < 4.\left( { - \frac{1}{2}} \right)\\x < - 2\end{array}\)
Vậy nghiệm của bất phương trình là \(x < - 2\).
Chú ý: Ta cũng có thể giải được các bất phương trình một ẩn đưa được về dạng \(ax + b < 0\), \(ax + b > 0\), \(ax + b \le 0\), \(ax + b \ge 0\).
Bất phương trình bậc nhất một ẩn là một biểu thức toán học chứa dấu bất đẳng thức (>, <, ≥, ≤) và một ẩn bậc nhất. Việc nắm vững lý thuyết về bất phương trình bậc nhất một ẩn là nền tảng quan trọng để giải quyết các bài toán thực tế và tiếp thu kiến thức toán học ở các lớp học cao hơn.
Bất phương trình bậc nhất một ẩn có dạng tổng quát: ax + b > 0 (hoặc < 0, ≥ 0, ≤ 0), trong đó:
Ví dụ: 2x + 3 > 0, -x - 5 ≤ 0, 0.5x + 1 < 2.
Để giải bất phương trình, chúng ta cần hiểu rõ các tính chất của bất đẳng thức:
Lưu ý quan trọng: Khi nhân hoặc chia cả hai vế của bất đẳng thức với một số âm, ta phải đổi chiều bất đẳng thức.
Dựa trên các tính chất của bất đẳng thức, chúng ta có thể áp dụng các quy tắc sau để biến đổi bất phương trình:
Để giải bất phương trình bậc nhất một ẩn, ta thực hiện các bước sau:
Ví dụ: Giải bất phương trình 2x + 3 > 0
Vậy nghiệm của bất phương trình là x > -3/2.
Hãy giải các bất phương trình sau:
Bất phương trình bậc nhất một ẩn được ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống, như:
Việc hiểu rõ lý thuyết và kỹ năng giải bất phương trình bậc nhất một ẩn sẽ giúp bạn tự tin hơn trong việc giải quyết các vấn đề thực tế và nâng cao khả năng tư duy logic.
Bài học về lý thuyết bất phương trình bậc nhất một ẩn Toán 9 Kết nối tri thức đã cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất. Hãy luyện tập thường xuyên để nắm vững kiến thức và áp dụng vào giải quyết các bài toán cụ thể. Chúc bạn học tốt!