Bài học này cung cấp kiến thức nền tảng về đường tròn ngoại tiếp và đường tròn nội tiếp của một tam giác trong chương trình Toán 9 Kết nối tri thức. Chúng ta sẽ cùng tìm hiểu định nghĩa, tính chất và cách xác định các đường tròn này.
Nắm vững lý thuyết này là bước quan trọng để giải quyết các bài toán liên quan đến tam giác và đường tròn, đồng thời xây dựng nền tảng vững chắc cho các kiến thức toán học nâng cao.
1. Đường tròn ngoại tiếp của một tam giác Định nghĩa đường tròn ngoại tiếp tam giác Đường tròn ngoại tiếp của một tam giác là đường tròn đi qua ba đỉnh của tam giác đó.
1. Đường tròn ngoại tiếp của một tam giác
Định nghĩa đường tròn ngoại tiếp tam giác
Đường tròn ngoại tiếp của một tam giác là đường tròn đi qua ba đỉnh của tam giác đó. |
Ví dụ:
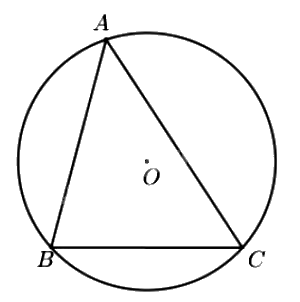
- Đường tròn (O) ngoại tiếp tam giác ABC. Tam giác ABC nội tiếp đường tròn (O).
- Tâm O là giao điểm của ba đường trung trực của tam giác ABC.
Đường tròn ngoại tiếp tam giác vuông
Đường tròn ngoại tiếp tam giác vuông có tâm là trung điểm của cạnh huyền và bán kính bằng một nửa cạnh huyền. |
Ví dụ:
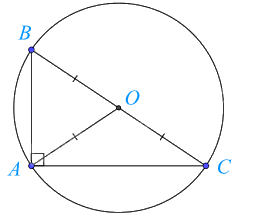
Tam giác ABC nội tiếp đường tròn (O; BO).
Đường tròn ngoại tiếp tam giác đều
Đường tròn ngoại tiếp tam giác đều cạnh a có tâm là trọng tâm của tam giác đó và bán kính bằng \(\frac{{\sqrt 3 }}{3}a\). |
Ví dụ:
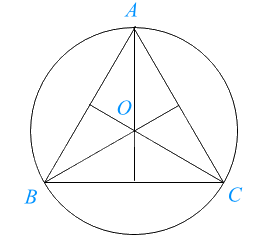
Đường tròn (O) ngoại tiếp tam giác đều ABC, bán kính \(OA = OB = OC = \frac{{\sqrt 3 }}{3}AB\).
2. Đường tròn nội tiếp một tam giác
Định nghĩa đường tròn nội tiếp tam giác
Đường tròn tiếp xúc với ba cạnh của tam giác được gọi là đường tròn nội tiếp tam giác. Tam giác đó được gọi là ngoại tiếp đường tròn. Tâm đường tròn nội tiếp tam giác là giao điểm ba đường phân giác của tam giác. |
Ví dụ:
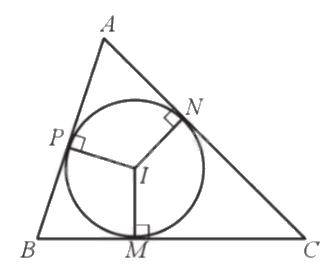
- Đường tròn (I) nội tiếp tam giác ABC. Tam giác ABC ngoại tiếp đường tròn (I).
- Tâm I là giao điểm của ba đường phân giác của tam giác.
Đường tròn nội tiếp tam giác đều
Đường tròn nội tiếp tam giác đều cạnh a có tâm là trọng tâm của tam giác đó và bán kính bằng \(\frac{{\sqrt 3 }}{6}a\). |
Ví dụ:
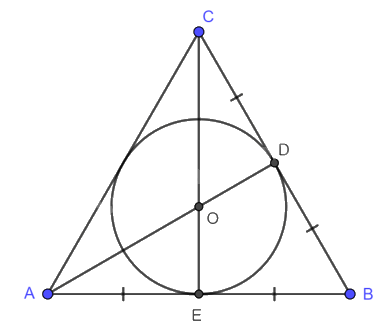
Đường tròn (O) nội tiếp tam giác đều ABC, bán kính \(OD = OE = \frac{{\sqrt 3 }}{6}AB\).
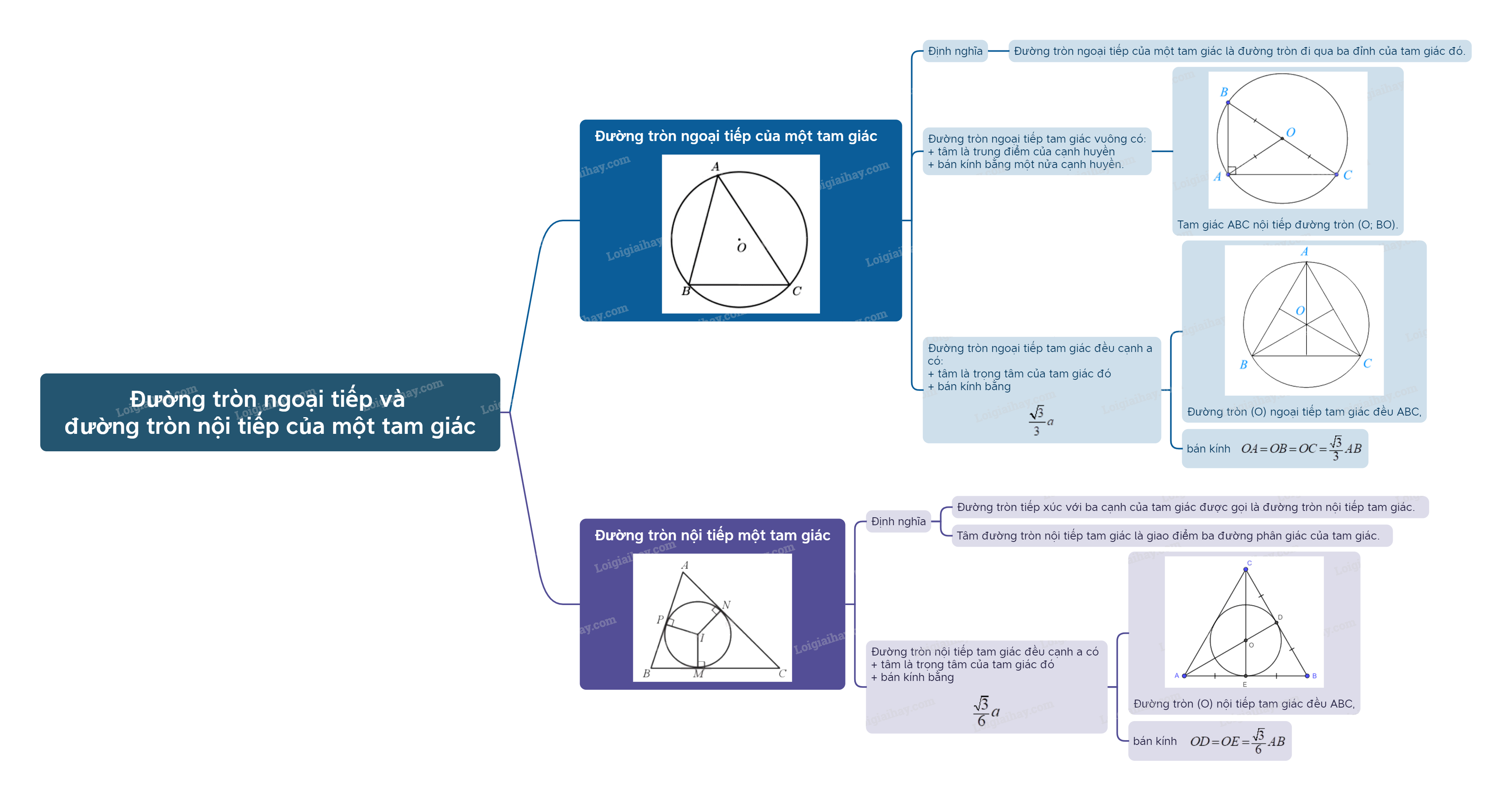
Trong hình học, đường tròn ngoại tiếp và đường tròn nội tiếp là hai khái niệm quan trọng liên quan đến tam giác. Chúng đóng vai trò then chốt trong việc giải quyết nhiều bài toán và có ứng dụng thực tế cao. Bài viết này sẽ trình bày chi tiết lý thuyết về hai loại đường tròn này trong chương trình Toán 9 Kết nối tri thức.
Định nghĩa: Đường tròn ngoại tiếp tam giác là đường tròn đi qua ba đỉnh của tam giác đó.
Tâm đường tròn ngoại tiếp: Giao điểm của các đường trung trực của tam giác. Tâm này được gọi là tâm đường tròn ngoại tiếp (O).
Bán kính đường tròn ngoại tiếp: Khoảng cách từ tâm O đến mỗi đỉnh của tam giác. Ký hiệu là R.
Công thức tính bán kính đường tròn ngoại tiếp (R):
Tính chất:
Định nghĩa: Đường tròn nội tiếp tam giác là đường tròn tiếp xúc với cả ba cạnh của tam giác.
Tâm đường tròn nội tiếp: Giao điểm của các đường phân giác của tam giác. Tâm này được gọi là tâm đường tròn nội tiếp (I).
Bán kính đường tròn nội tiếp: Khoảng cách từ tâm I đến mỗi cạnh của tam giác. Ký hiệu là r.
Công thức tính bán kính đường tròn nội tiếp (r):
Tính chất:
Trong một tam giác, đường tròn ngoại tiếp và đường tròn nội tiếp có mối quan hệ mật thiết với nhau. Chúng cùng nhau xác định các tính chất quan trọng của tam giác.
Công thức Euler: d2 = R(R - 2r), trong đó d là khoảng cách giữa tâm đường tròn ngoại tiếp và tâm đường tròn nội tiếp, R là bán kính đường tròn ngoại tiếp và r là bán kính đường tròn nội tiếp.
Bài tập 1: Cho tam giác ABC có AB = 3cm, BC = 4cm, CA = 5cm. Tính bán kính đường tròn ngoại tiếp và đường tròn nội tiếp của tam giác ABC.
Giải:
Bài tập 2:...
Lý thuyết về đường tròn ngoại tiếp và đường tròn nội tiếp là một phần quan trọng của chương trình Toán 9 Kết nối tri thức. Việc nắm vững các định nghĩa, tính chất và công thức liên quan sẽ giúp học sinh giải quyết các bài toán một cách hiệu quả và xây dựng nền tảng vững chắc cho các kiến thức toán học tiếp theo.