Bài tập 7.9 trang 42 SGK Toán 9 tập 2 thuộc chương trình Kết nối tri thức là một bài toán quan trọng giúp học sinh rèn luyện kỹ năng về hàm số bậc nhất và ứng dụng của nó. Bài viết này sẽ cung cấp lời giải chi tiết, dễ hiểu cùng với các kiến thức liên quan để bạn có thể tự tin giải quyết bài toán này.
Giaitoan.edu.vn luôn đồng hành cùng học sinh trong quá trình học tập, cung cấp các tài liệu và lời giải bài tập Toán 9 chính xác, nhanh chóng và hiệu quả.
Theo Tổng cục Thống kê, vào năm 2021 trong số 50,5 triệu lao động Việt Nam từ 15 tuổi trở lên có 13,9 triệu lao động đang làm việc trong lĩnh vực nông nghiệp, lâm nghiệp và thủy sản; 16,9 triệu lao động đang làm việc trong lĩnh vực công nghiệp và xây dựng; 19,7 triệu lao động đang làm việc trong lĩnh vực dịch vụ. a) Lập bảng tần số tương đối cho dữ liệu trên. b) Vẽ biểu đồ hình quạt tròn biểu diễn bảng tần số tương đối thu được ở câu a. c) Tính tỉ lệ lao động không làm việc trong lĩnh vực nôn
Đề bài
Theo Tổng cục Thống kê, vào năm 2021 trong số 50,5 triệu lao động Việt Nam từ 15 tuổi trở lên có 13,9 triệu lao động đang làm việc trong lĩnh vực nông nghiệp, lâm nghiệp và thủy sản; 16,9 triệu lao động đang làm việc trong lĩnh vực công nghiệp và xây dựng; 19,7 triệu lao động đang làm việc trong lĩnh vực dịch vụ.
a) Lập bảng tần số tương đối cho dữ liệu trên.
b) Vẽ biểu đồ hình quạt tròn biểu diễn bảng tần số tương đối thu được ở câu a.
c) Tính tỉ lệ lao động không làm việc trong lĩnh vực nông nghiệp, lâm nghiệp và thủy sản.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) + Tính tần số tương đối ứng với các giá trị trong mẫu dữ liệu: Giá trị \({x_i}\) có tần số \({m_i}\) thì có tần số tương đối là: \({f_i} = \frac{{{m_i}}}{n}.100\left( \% \right)\) với m là tổng tất cả các tần số có trong mẫu số liệu.
+ Lập bảng tần số tương đối:

Cách vẽ biểu đồ tần số tương đối:
Bước 1: Xác định số đo cung tương ứng của các hình quạt dùng để biểu diễn tần số tương đối của các giá trị theo công thức \({360^o}.{f_i}\) với \(i = 1,...,k\)
Bước 2: Vẽ hình tròn và chia hình tròn thành các hình quạt có số đo cung tương ứng được xác định trong Bước 1.
Bước 3: Định dạng các hình quạt tròn (thường bằng cách tô màu), ghi tần số tương đối, chú giải và tiêu đề.
c) Tỉ lệ lao động không làm việc trong lĩnh vực Nông nghiệp, lâm nghiệp và thủy sản= \(100\% - \) tỉ lệ lao động làm trong lĩnh Nông nghiệp, lâm nghiệp và thủy sản.
Lời giải chi tiết
a) Tần số tương đối của số lao động làm việc trong lĩnh vực nông nghiệp, lâm nghiệp và thủy sản; công nghiệp và công nghiệp; dịch vụ lần lượt là:
\({f_1} = \frac{{13,9}}{{50,5}} \approx 27,5\% ,{f_2} = \frac{{16,9}}{{50,5}} \approx 33,5\% ;{f_3} = \frac{{19,7}}{{50,5}} \approx 39\% \)

b) Bước 1: Xác định số đo cung tương ứng của các hình quạt biểu diễn các tần số tương đối của các lĩnh vực:
Nông nghiệp, lâm nghiệp và thủy sản: \({360^o}.27,5\% = {99^o}\),
Công nghiệp và xây dựng: \({360^o}.33,5\% = 120,{6^o}\),
Dịch vụ: \({360^o}.39\% = 140,{4^o}\).
Bước 2: Vẽ hình tròn và chia hình tròn thành các hình quạt
Bước 3: Định dạng các hình quạt tròn, ghi tỉ lệ phần trăm, chú giải và tiêu đề.
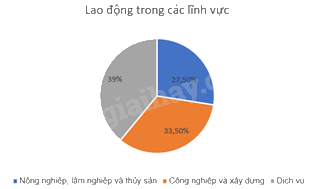
c) Tỉ lệ lao động không làm việc trong lĩnh vực nông nghiệp, lâm nghiệp và thủy sản là: \(100\% - 27,5\% = 72,5\% \)
Bài tập 7.9 trang 42 SGK Toán 9 tập 2 yêu cầu chúng ta xét hàm số bậc nhất và xác định hệ số góc. Để giải bài tập này, chúng ta cần nắm vững các kiến thức cơ bản về hàm số bậc nhất, bao gồm:
Bài tập 7.9 thường có dạng yêu cầu xác định hệ số góc của đường thẳng đi qua hai điểm cho trước, hoặc xác định hàm số bậc nhất khi biết hệ số góc và một điểm thuộc đường thẳng.
Ví dụ: Cho hai điểm A(1; 2) và B(3; 6). Hãy tìm hệ số góc của đường thẳng AB.
Giải:
Ngoài bài tập 7.9, còn rất nhiều bài tập tương tự yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất. Dưới đây là một số dạng bài tập thường gặp và phương pháp giải:
Để giải bài tập về hàm số bậc nhất một cách hiệu quả, bạn cần lưu ý những điều sau:
Hàm số bậc nhất có rất nhiều ứng dụng trong thực tế, ví dụ như:
Bài tập 7.9 trang 42 SGK Toán 9 tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất. Hy vọng với hướng dẫn chi tiết và các ví dụ minh họa trên, bạn đã có thể tự tin giải quyết bài tập này và các bài tập tương tự. Chúc bạn học tập tốt!