Bài tập 10.23 trang 108 SGK Toán 9 tập 2 thuộc chương trình Toán 9 Kết nối tri thức, yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế. Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu, giúp các em học sinh hiểu rõ phương pháp và tự tin làm bài.
Chúng tôi luôn cập nhật nhanh chóng và chính xác lời giải các bài tập trong SGK Toán 9 tập 2, đảm bảo hỗ trợ tối đa cho quá trình học tập của các em.
Cho hình nón có bán kính đáy bằng 9cm, độ dài đường sinh bằng 15cm (H.10.34). a) Tính diện tích xung quanh của hình nón. b) Tính thể tích của hình nón. c) Diện tích toàn phần của hình nón bằng tổng diện tích xung quanh và diện tích đáy. Tính diện tích toàn phần của hình nón đã cho.
Đề bài
Cho hình nón có bán kính đáy bằng 9cm, độ dài đường sinh bằng 15cm (H.10.34).
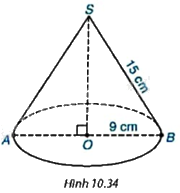
a) Tính diện tích xung quanh của hình nón.
b) Tính thể tích của hình nón.
c) Diện tích toàn phần của hình nón bằng tổng diện tích xung quanh và diện tích đáy. Tính diện tích toàn phần của hình nón đã cho.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Diện tích xung quanh của hình nón bán kính đáy r và độ dài đường sinh l là: \({S_{xq}} = \pi rl\).
b) Thể tích của hình nón bán kính đáy r và chiều cao h là: \(V = \frac{1}{3}\pi {r^2}h\).
c) + Diện tích đáy hình nón là: \(S = \pi {r^2}\).
+ Diện tích toàn phần của hình nón bằng tổng diện tích xung quanh và diện tích đáy.
Lời giải chi tiết
Xét hình nón có đường sinh \(SB = 15cm\) và bán kính đáy \(OB = 9cm\).
Tam giác SOB vuông tại O nên \(S{O^2} + O{B^2} = S{B^2}\)
\({9^2} + S{O^2} = {15^2}\)
\(SO = 12cm\)
a) Diện tích xung quanh của hình nón là:
\({S_{xq}} = \pi .OB.SB = 9.15.\pi = 135\pi \left( {c{m^2}} \right)\).
b) Thể tích của hình nón là:
\(V = \frac{1}{3}\pi .O{B^2}.SO = \frac{1}{3}{.9^2}.12.\pi = 324\pi \left( {c{m^3}} \right)\).
c) Diện tích đáy hình nón là:
\({S_{đáy}} = \pi .O{B^2} = {9^2}\pi = 81\pi \left( {c{m^2}} \right)\).
Diện tích toàn phần của hình nón là:
\(S = {S_{xq}} + {S_{đáy}} = 135\pi + 81\pi = 216\pi \left( {c{m^2}} \right)\).
Bài tập 10.23 SGK Toán 9 tập 2 Kết nối tri thức là một bài toán ứng dụng thực tế, yêu cầu học sinh sử dụng kiến thức về hàm số bậc hai để giải quyết. Để giải bài tập này, chúng ta cần nắm vững các khái niệm cơ bản về hàm số bậc hai, bao gồm:
Trước khi bắt tay vào giải bài tập, chúng ta cần đọc kỹ đề bài, xác định rõ yêu cầu và các dữ kiện đã cho. Bài tập 10.23 thường yêu cầu chúng ta:
(Ở đây sẽ là lời giải chi tiết của bài tập 10.23, bao gồm các bước giải, giải thích rõ ràng và ví dụ minh họa. Lời giải sẽ được trình bày một cách logic và dễ hiểu, giúp học sinh nắm vững phương pháp giải.)
Để giúp các em hiểu rõ hơn về cách giải bài tập 10.23, chúng ta sẽ cùng xem xét một số ví dụ minh họa. Sau đó, chúng ta sẽ đưa ra một số bài tập tương tự để các em tự luyện tập.
Ví dụ 1: Một vật được ném lên từ mặt đất với vận tốc ban đầu là 15 m/s. Hãy viết phương trình mô tả quỹ đạo của vật và tìm độ cao lớn nhất mà vật đạt được.
Giải:
Gọi x là khoảng cách ngang từ điểm ném đến vật và y là độ cao của vật. Phương trình mô tả quỹ đạo của vật có dạng y = ax2 + bx + c. Vì vật được ném từ mặt đất, nên c = 0. Vận tốc ban đầu là 15 m/s, nên b = 15. Gia tốc trọng trường là g = 9.8 m/s2, nên a = -4.9. Vậy phương trình quỹ đạo của vật là y = -4.9x2 + 15x.
Đỉnh của Parabol là điểm có hoành độ x = -b/(2a) = -15/(2*(-4.9)) ≈ 1.53. Độ cao lớn nhất mà vật đạt được là y = -4.9*(1.53)2 + 15*1.53 ≈ 11.48 m.
Bài tập 10.23 trang 108 SGK Toán 9 tập 2 Kết nối tri thức là một bài toán ứng dụng thực tế, giúp học sinh hiểu rõ hơn về hàm số bậc hai và ứng dụng của nó trong cuộc sống. Hy vọng rằng với lời giải chi tiết và các ví dụ minh họa trên, các em học sinh sẽ tự tin hơn khi giải các bài tập tương tự.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!