Bài tập 9.35 trang 91 SGK Toán 9 tập 2 thuộc chương trình Toán 9 Kết nối tri thức, yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế. Bài tập này thường gặp trong các kỳ thi và kiểm tra, do đó việc nắm vững phương pháp giải là vô cùng quan trọng.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 9.35 trang 91 SGK Toán 9 tập 2, giúp các em học sinh hiểu rõ bản chất của bài toán và tự tin làm bài.
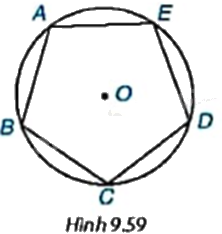
Cho ngũ giác đều ABCDE nội tiếp đường tròn (O) như Hình 9.59. a) Hãy tìm một phép quay thuận chiều tâm O biến điểm A thành điểm C. b) Phép quay trên sẽ biến các điểm B, C, D, E lần lượt thành những điểm nào? Phép quay này có giữ nguyên ngũ giác đều ABCDE không?
Đề bài
Cho ngũ giác đều ABCDE nội tiếp đường tròn (O) như Hình 9.59.
a) Hãy tìm một phép quay thuận chiều tâm O biến điểm A thành điểm C.
b) Phép quay trên sẽ biến các điểm B, C, D, E lần lượt thành những điểm nào? Phép quay này có giữ nguyên ngũ giác đều ABCDE không?
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+ Phép quay thuận chiều \({\alpha ^o}\left( {{0^o} < {\alpha ^o} < {{360}^o}} \right)\) tâm O giữ nguyên điểm O, biến điểm A khác điểm O thành điểm B thuộc đường tròn (O; OA) sao cho tia OA quay thuận chiều kim đồng hồ đến tia OB thì điểm A tạo nên cung AB có số đo \({\alpha ^o}\).
+ Một phép quay được gọi là giữ nguyên một đa giác đều H nếu phép quay đó biến mỗi điểm của H thành một điểm của H.
Lời giải chi tiết
a) Phép quay chiều thuận \({216^o}\) tâm O biến điểm A thành điểm C.
b) Phép quay chiều thuận \({216^o}\) tâm O biến điểm E thành điểm B, điểm D thành điểm A, điểm C thành điểm E, điểm B thành điểm D. Do đó, phép quay này giữ nguyên ngũ giác đều ABCDE.
Bài tập 9.35 trang 91 SGK Toán 9 tập 2 yêu cầu học sinh giải một bài toán thực tế liên quan đến hàm số bậc hai. Để giải bài tập này, chúng ta cần:
Giả sử bài toán yêu cầu tìm chiều cao tối đa mà một quả bóng có thể đạt được khi được ném lên từ mặt đất với vận tốc ban đầu là 15 m/s. Ta có thể mô tả chiều cao của quả bóng bằng hàm số bậc hai:
h(t) = -5t2 + 15t
Trong đó:
Để tìm chiều cao tối đa, ta cần tìm đỉnh của parabol. Tọa độ đỉnh của parabol được tính bằng công thức:
xđỉnh = -b / 2a
Trong trường hợp này, a = -5 và b = 15, do đó:
xđỉnh = -15 / (2 * -5) = 1.5
Chiều cao tối đa của quả bóng là:
h(1.5) = -5 * (1.5)2 + 15 * 1.5 = 11.25
Vậy chiều cao tối đa mà quả bóng có thể đạt được là 11.25 mét.
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải bài tập 9.35 trang 91 SGK Toán 9 tập 2 - Kết nối tri thức và đạt kết quả tốt trong môn Toán.