Chào mừng bạn đến với bài học về Lý thuyết Góc nội tiếp Toán 9 Kết nối tri thức tại giaitoan.edu.vn. Bài viết này sẽ cung cấp cho bạn kiến thức nền tảng, các định lý quan trọng và phương pháp giải bài tập liên quan đến góc nội tiếp một cách chi tiết và dễ hiểu.
Góc nội tiếp là một khái niệm quan trọng trong chương trình hình học lớp 9, đóng vai trò then chốt trong việc giải quyết nhiều bài toán thực tế. Việc nắm vững lý thuyết này sẽ giúp bạn tự tin hơn khi đối mặt với các bài kiểm tra và kỳ thi.
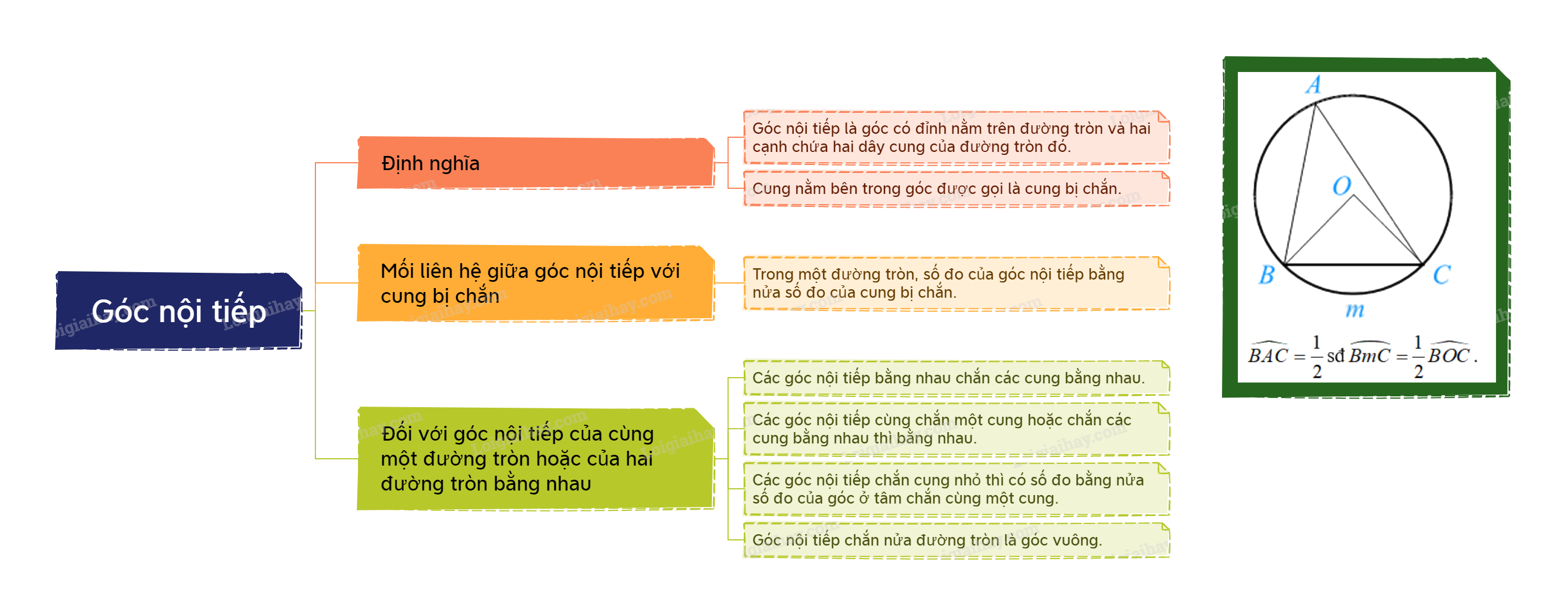
Định nghĩa góc nội tiếp Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó. Cung nằm bên trong góc được gọi là cung bị chắn.
Định nghĩa góc nội tiếp
Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó. Cung nằm bên trong góc được gọi là cung bị chắn. |
Ví dụ:
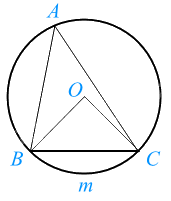
- Góc BAC là góc nội tiếp của đường tròn (O);
- Góc nội tiếp BAC chắn cung $\overset\frown{BmC}$.
Định lí mối liên hệ giữa góc nội tiếp với cung bị chắn
Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo của cung bị chắn. |
Ví dụ:
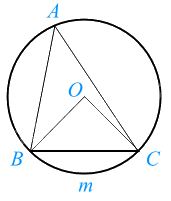
\(\widehat {BAC} = \frac{1}{2}\)sđ$\overset\frown{BmC}=\frac{1}{2}\widehat{BOC}$.
Nhận xét: Đối với góc nội tiếp của cùng một đường tròn hoặc của hai đường tròn bằng nhau, ta có các khẳng định sau:
+ Các góc nội tiếp bằng nhau chắn các cung bằng nhau.
+ Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
+ Các góc nội tiếp chắn cung nhỏ thì có số đo bằng nửa số đo của góc ở tâm chắn cùng một cung.
+ Góc nội tiếp chắn nửa đường tròn là góc vuông.
Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai điểm khác nhau trên đường tròn. Hiểu rõ định nghĩa này là bước đầu tiên để nắm vững toàn bộ lý thuyết về góc nội tiếp.
Để hiểu rõ hơn về góc nội tiếp, chúng ta cần nắm vững các thuật ngữ sau:
Góc nội tiếp bằng nửa số đo của cung bị chắn. Điều này có nghĩa là nếu góc nội tiếp chắn cung AmB, thì số đo của góc nội tiếp bằng một nửa số đo của cung AmB.
Các góc nội tiếp cùng chắn một cung thì bằng nhau. Đây là một định lý quan trọng giúp chúng ta chứng minh sự bằng nhau của các góc trong các bài toán hình học.
Góc nội tiếp chắn nửa đường tròn là góc vuông. Định lý này thường được sử dụng để chứng minh các tam giác vuông nội tiếp đường tròn.
Tứ giác có tổng hai góc đối nhau bằng 180° là tứ giác nội tiếp đường tròn. Đây là một dấu hiệu nhận biết quan trọng của tứ giác nội tiếp.
Nếu hai cung song song chắn hai góc nội tiếp thì hai góc nội tiếp đó bằng nhau.
Ví dụ 1: Cho đường tròn (O) và góc nội tiếp ∠ABC = 60°. Tính số đo cung AC.
Giải: Theo định lý, số đo cung AC = 2 * ∠ABC = 2 * 60° = 120°.
Ví dụ 2: Cho tứ giác ABCD nội tiếp đường tròn. Biết ∠A = 80° và ∠C = 100°. Chứng minh tứ giác ABCD là tứ giác nội tiếp.
Giải: Ta có ∠A + ∠C = 80° + 100° = 180°. Do đó, tứ giác ABCD là tứ giác nội tiếp.
Để củng cố kiến thức, bạn hãy thử giải các bài tập sau:
Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về Lý thuyết Góc nội tiếp Toán 9 Kết nối tri thức. Hãy luyện tập thường xuyên để nắm vững kiến thức và tự tin giải các bài tập liên quan. Chúc bạn học tốt!