Bài tập 8.12 trang 66 SGK Toán 9 tập 2 thuộc chương trình Toán 9 Kết nối tri thức, yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai và đồ thị của hàm số để giải quyết các bài toán thực tế. Bài tập này thường gặp trong các kỳ thi và kiểm tra, do đó việc nắm vững phương pháp giải là vô cùng quan trọng.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 8.12 trang 66 SGK Toán 9 tập 2, giúp các em học sinh hiểu rõ bản chất của bài toán và tự tin giải các bài tập tương tự.
Gieo đồng thời hai con xúc xắc cân đối, đồng chất. Xác suất để “Tổng số chấm xuất hiện trên hai con xúc xắc lớn hơn hoặc bằng 10” là A. (frac{7}{{36}}). B. (frac{2}{9}). C. (frac{1}{6}). D. (frac{5}{{36}}).
Đề bài
Gieo đồng thời hai con xúc xắc cân đối, đồng chất. Xác suất để “Tổng số chấm xuất hiện trên hai con xúc xắc lớn hơn hoặc bằng 10” là
A. \(\frac{7}{{36}}\).
B. \(\frac{2}{9}\).
C. \(\frac{1}{6}\).
D. \(\frac{5}{{36}}\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Cách tính xác suất của một biến cố E:
Bước 1. Mô tả không gian mẫu của phép thử. Từ đó xác định số phần tử của không gian mẫu \(\Omega \).
Bước 2. Chứng tỏ các kết quả có thể của phép thử là đồng khả năng.
Bước 3. Mô tả kết quả thuận lợi của biến cố E. Từ đó xác định số kết quả thuận lợi cho biến cố E.
Bước 4. Lập tỉ số giữa số kết quả thuận lợi cho biến cố E với số phần tử của không gian mẫu \(\Omega \).
Lời giải chi tiết
Kết quả phép thử được viết dưới dạng (a, b) trong đó a, b lần lượt là số chấm xuất hiện trên hai con xúc xắc I và II.
Ta có bảng miêu tả không gian mẫu là:
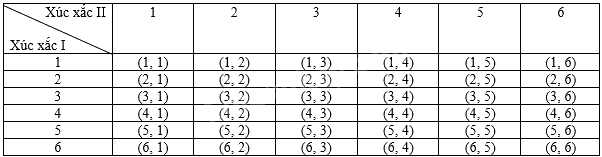
Do đó, số phần tử của không gian mẫu \(\Omega \) là 36.
Vì gieo đồng thời hai con xúc xắc cân đối, đồng chất nên các kết quả có thể xảy ra là đồng khả năng.
Có 6 kết quả thuận lợi của biến cố “Tổng số chấm xuất hiện trên hai con xúc xắc lớn hơn hoặc bằng 10” là: (4, 6), (5, 5), (5, 6), (6, 4), (6, 5), (6, 6). Do đó, \(P = \frac{6}{{36}} = \frac{1}{6}\).
Chọn C
Bài tập 8.12 SGK Toán 9 tập 2 Kết nối tri thức yêu cầu học sinh giải một bài toán thực tế liên quan đến hàm số bậc hai. Để giải bài tập này, chúng ta cần nắm vững các kiến thức sau:
Bài toán 8.12 thường mô tả một tình huống thực tế, ví dụ như quỹ đạo của một vật được ném lên, hoặc sự thay đổi của một đại lượng theo thời gian. Để giải bài toán, chúng ta cần:
Đề bài: Một quả bóng được ném lên từ mặt đất với vận tốc ban đầu là 15 m/s. Giả sử rằng quả bóng chuyển động theo quỹ đạo là một parabol. Hãy viết phương trình mô tả quỹ đạo của quả bóng và tìm độ cao lớn nhất mà quả bóng đạt được.
Giải:
Chọn hệ tọa độ Oxy với gốc O tại vị trí ném bóng, trục Ox nằm ngang và trục Oy hướng lên trên. Phương trình mô tả quỹ đạo của quả bóng có dạng y = ax2 + bx + c.
Vì quả bóng được ném từ mặt đất, nên c = 0. Vận tốc ban đầu của quả bóng là 15 m/s, nên b = 15. Gia tốc trọng trường là g = 9.8 m/s2, nên a = -4.9. Vậy phương trình quỹ đạo của quả bóng là:
y = -4.9x2 + 15x
Để tìm độ cao lớn nhất mà quả bóng đạt được, ta cần tìm tọa độ đỉnh của parabol. Ta có:
x0 = -b/2a = -15/(2 * -4.9) ≈ 1.53
y0 = -4.9 * (1.53)2 + 15 * 1.53 ≈ 11.48
Vậy độ cao lớn nhất mà quả bóng đạt được là khoảng 11.48 mét.
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải bài tập 8.12 trang 66 SGK Toán 9 tập 2 - Kết nối tri thức. Chúc các em học tập tốt!