Bài tập 10.15 trang 107 SGK Toán 9 tập 2 thuộc chương trình Toán 9 Kết nối tri thức, yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế. Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu, giúp các em học sinh hiểu rõ phương pháp và tự tin làm bài.
Chúng tôi luôn cập nhật nhanh chóng và chính xác lời giải các bài tập trong SGK Toán 9 tập 2, đảm bảo hỗ trợ tối đa cho quá trình học tập của các em.
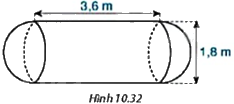
Một bồn chứa xăng gồm hai nửa hình cầu có đường kính bằng 1,8m và một hình trụ có chiều cao bằng 3,6m (H.10.32). Tính thể tích của bồn chứa xăng (làm tròn kết quả đến hàng phần trăm của ({m^3})).
Đề bài
Một bồn chứa xăng gồm hai nửa hình cầu có đường kính bằng 1,8m và một hình trụ có chiều cao bằng 3,6m (H.10.32). Tính thể tích của bồn chứa xăng (làm tròn kết quả đến hàng phần trăm của \({m^3}\)).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+ Bán kính hai nửa hình cầu là \(\frac{{1,8}}{2} = 0,9\left( m \right)\).
+ Tính thể tích \({V_1}\) hình trụ chiều cao 3,6m và bán kính 0,9m.
+ Tính thể tích \({V_2}\) hai nửa hình cầu bán kính 0,9m.
+ Thể tích bồn chứa xăng: \(V = {V_1} + {V_2}\).
Lời giải chi tiết
Bán kính hai nửa hình cầu là \(\frac{{1,8}}{2} = 0,9\left( m \right).\)
Thể tích hình trụ chiều cao 3,6m và bán kính 0,9m là:
\({V_1} = \pi .0,{9^2}.3,6 = 2,916\pi \left( {{m^3}} \right).\)
Thể thể tích hai nửa hình cầu bán kính 0,9m là:
\({V_2} = \frac{4}{3}.\pi .0,{9^3} = 0,972\pi \left( {{m^3}} \right).\)
Thể tích bồn chứa xăng là:
\(V = {V_1} + {V_2} = 2,916\pi + 0,972\pi = 3,888\pi \approx 12,21\left( {{m^3}} \right).\)
Bài tập 10.15 trang 107 SGK Toán 9 tập 2 yêu cầu học sinh giải một bài toán thực tế liên quan đến hàm số bậc hai. Để giải bài tập này, chúng ta cần nắm vững các kiến thức sau:
Bài toán 10.15 thường mô tả một tình huống thực tế, ví dụ như việc ném một vật thể lên cao, hoặc quỹ đạo của một quả bóng. Bài toán yêu cầu chúng ta xác định phương trình của parabol mô tả quỹ đạo của vật thể, hoặc tìm các thông số của parabol như đỉnh, trục đối xứng, tiêu điểm, đường chuẩn.
Để giải bài tập này, chúng ta thực hiện các bước sau:
Giả sử bài toán yêu cầu tìm phương trình của parabol có đỉnh là (1; 2) và đi qua điểm (0; 1). Chúng ta có thể giải bài toán này như sau:
Phương trình của parabol có dạng y = a(x - h)2 + k, với (h; k) là tọa độ đỉnh của parabol. Trong trường hợp này, h = 1 và k = 2, do đó phương trình của parabol có dạng y = a(x - 1)2 + 2.
Vì parabol đi qua điểm (0; 1), chúng ta thay x = 0 và y = 1 vào phương trình để tìm a:
1 = a(0 - 1)2 + 2 => 1 = a + 2 => a = -1.
Vậy phương trình của parabol là y = - (x - 1)2 + 2.
Bài tập 10.15 trang 107 SGK Toán 9 tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc hai và ứng dụng của nó trong giải quyết các bài toán thực tế. Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục kiến thức Toán học. Chúc các em học tập tốt!