Giaitoan.edu.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 2 trang 85, 86 sách giáo khoa Toán 9 tập 1 chương trình Kết nối tri thức. Bài viết này sẽ giúp các em học sinh nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi luôn cố gắng cung cấp những giải pháp học tập tốt nhất, giúp các em học Toán 9 một cách hiệu quả và thú vị.
Chứng minh rằng nếu một điểm thuộc đường tròn (O) thì: a) Điểm đối xứng với nó qua tâm O cũng thuộc (O). b) Điểm đối xứng với nó qua một đường thẳng d tùy ý đi qua O cũng thuộc (O).
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 2 trang 86 SGK Toán 9 Kết nối tri thức
Trở lại tình huống mở đầu, bằng cách gấp mảnh giấy hình tròn theo hai cách khác nhau, Oanh có thể tìm được tâm của hình tròn. Em hãy làm thử xem.
Phương pháp giải:
Tình huống mở đầu: Bạn Oanh có một mảnh giấy hình tròn nhưng không còn dấu vết của tâm, Theo em, Oanh làm thế nào để tìm lại được tâm của hình tròn đó.
Khi gấp đôi hình tròn ta được đường kính, khi ta thực hiện 2 lần gấp như vậy theo 2 cách khác nhau ta được hai đường kính, mà hai đường kính sẽ giao nhau tại tâm của hình tròn. Từ đó ta xác định được tâm của hình tròn.
Lời giải chi tiết:
Gấp đôi hình tròn sao cho mép giấy của chúng đè khít lên nhau, ta miết phần ngăn cách hai nửa hình tròn ta được 1 đường kính, tiếp theo mở tờ giấy và gấp theo hướng khác, ta làm như vậy và xác định được đường kính mới, hai đường kính này cắt nhau tại tâm của hình tròn.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động trang 85 SGK Toán 9 Kết nối tri thức
Chứng minh rằng nếu một điểm thuộc đường tròn (O) thì:
a) Điểm đối xứng với nó qua tâm O cũng thuộc (O).
b) Điểm đối xứng với nó qua một đường thẳng d tùy ý đi qua O cũng thuộc (O).
Phương pháp giải:
a) Lấy điểm A bất kì thuộc (O).
Gọi A’ là điểm đối xứng với A qua O. Chứng minh OA = OA’ = R
b) Lấy điểm M bất kì thuộc (O).
Gọi M’ là điểm đối xứng với M qua d. Chứng minh OM = OM’ = R
Lời giải chi tiết:
a) Lấy điểm A bất kì thuộc (O)
Gọi A’ là điểm đối xứng với A qua O.
Khi đó: O là trung điểm của AA’ hay OA = OA’ = R
⇒ A' cũng thuộc đường tròn (O)
b)
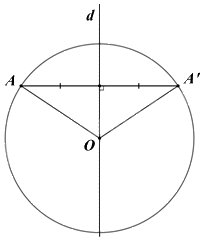
Lấy điểm A bất kì thuộc (O).
Gọi A’ là điểm đối xứng với A qua d.
Suy ra d là trung trực của AA'.
Mà \(O \in d\) nên OA = OA' = R.
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 2 trang 86 SGK Toán 9 Kết nối tri thức
Cho đường tròn tâm O và hai điểm A, B thuộc (O). Gọi d là đường trung trực của đoạn AB. Chứng minh rằng d là một trục đối xứng của (O).
Phương pháp giải:
Chứng minh d đi qua tâm O.
Lời giải chi tiết:
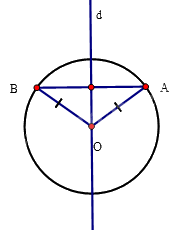
Vì OA = OB nên O thuộc d.
Vậy d là một trục đối xứng của (O).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động trang 85 SGK Toán 9 Kết nối tri thức
Chứng minh rằng nếu một điểm thuộc đường tròn (O) thì:
a) Điểm đối xứng với nó qua tâm O cũng thuộc (O).
b) Điểm đối xứng với nó qua một đường thẳng d tùy ý đi qua O cũng thuộc (O).
Phương pháp giải:
a) Lấy điểm A bất kì thuộc (O).
Gọi A’ là điểm đối xứng với A qua O. Chứng minh OA = OA’ = R
b) Lấy điểm M bất kì thuộc (O).
Gọi M’ là điểm đối xứng với M qua d. Chứng minh OM = OM’ = R
Lời giải chi tiết:
a) Lấy điểm A bất kì thuộc (O)
Gọi A’ là điểm đối xứng với A qua O.
Khi đó: O là trung điểm của AA’ hay OA = OA’ = R
⇒ A' cũng thuộc đường tròn (O)
b)
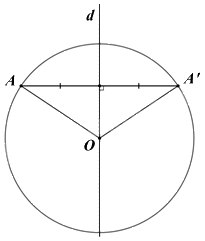
Lấy điểm A bất kì thuộc (O).
Gọi A’ là điểm đối xứng với A qua d.
Suy ra d là trung trực của AA'.
Mà \(O \in d\) nên OA = OA' = R.
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 2 trang 86 SGK Toán 9 Kết nối tri thức
Cho đường tròn tâm O và hai điểm A, B thuộc (O). Gọi d là đường trung trực của đoạn AB. Chứng minh rằng d là một trục đối xứng của (O).
Phương pháp giải:
Chứng minh d đi qua tâm O.
Lời giải chi tiết:
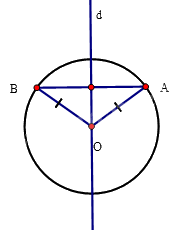
Vì OA = OB nên O thuộc d.
Vậy d là một trục đối xứng của (O).
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 2 trang 86 SGK Toán 9 Kết nối tri thức
Trở lại tình huống mở đầu, bằng cách gấp mảnh giấy hình tròn theo hai cách khác nhau, Oanh có thể tìm được tâm của hình tròn. Em hãy làm thử xem.
Phương pháp giải:
Tình huống mở đầu: Bạn Oanh có một mảnh giấy hình tròn nhưng không còn dấu vết của tâm, Theo em, Oanh làm thế nào để tìm lại được tâm của hình tròn đó.
Khi gấp đôi hình tròn ta được đường kính, khi ta thực hiện 2 lần gấp như vậy theo 2 cách khác nhau ta được hai đường kính, mà hai đường kính sẽ giao nhau tại tâm của hình tròn. Từ đó ta xác định được tâm của hình tròn.
Lời giải chi tiết:
Gấp đôi hình tròn sao cho mép giấy của chúng đè khít lên nhau, ta miết phần ngăn cách hai nửa hình tròn ta được 1 đường kính, tiếp theo mở tờ giấy và gấp theo hướng khác, ta làm như vậy và xác định được đường kính mới, hai đường kính này cắt nhau tại tâm của hình tròn.
Mục 2 trang 85, 86 SGK Toán 9 tập 1 - Kết nối tri thức tập trung vào việc ôn tập chương 1: Số thực. Nội dung chính bao gồm các dạng bài tập về căn bậc hai, căn bậc ba, biểu thức chứa căn, và các phép biến đổi đơn giản. Việc nắm vững kiến thức này là nền tảng quan trọng cho các chương học tiếp theo.
Mục 2 bao gồm một số bài tập rèn luyện kỹ năng tính toán và vận dụng kiến thức đã học. Dưới đây là phân tích chi tiết từng bài:
Bài tập này yêu cầu học sinh tính giá trị của các biểu thức chứa căn bậc hai và căn bậc ba. Để giải bài tập này, học sinh cần nắm vững các quy tắc về căn thức và phép tính với căn thức.
Bài tập này yêu cầu học sinh rút gọn các biểu thức chứa căn thức. Để giải bài tập này, học sinh cần sử dụng các quy tắc về rút gọn căn thức và các phép biến đổi đại số.
Bài tập này yêu cầu học sinh tìm giá trị của x thỏa mãn một phương trình chứa căn thức. Để giải bài tập này, học sinh cần sử dụng các phương pháp giải phương trình và các quy tắc về căn thức.
Để giải các bài tập về căn thức một cách hiệu quả, học sinh cần:
Khi giải các bài tập chứa căn thức, học sinh cần lưu ý:
Để củng cố kiến thức và rèn luyện kỹ năng, học sinh có thể tự giải thêm các bài tập nâng cao về căn thức. Các bài tập này thường có độ khó cao hơn và đòi hỏi học sinh phải vận dụng linh hoạt các kiến thức đã học.
Việc giải mục 2 trang 85, 86 SGK Toán 9 tập 1 - Kết nối tri thức là một bước quan trọng trong quá trình học Toán 9. Hy vọng rằng với những hướng dẫn chi tiết và phương pháp giải hiệu quả mà chúng tôi đã cung cấp, các em học sinh sẽ tự tin hơn trong việc giải các bài tập về căn thức và đạt kết quả tốt trong môn Toán.
| Bài tập | Nội dung chính | Phương pháp giải |
|---|---|---|
| Bài 1 | Tính giá trị biểu thức | Sử dụng quy tắc căn thức |
| Bài 2 | Rút gọn biểu thức | Rút gọn căn thức, biến đổi đại số |
| Bài 3 | Tìm x | Giải phương trình chứa căn thức |