Chào mừng các em học sinh đến với bài giải chi tiết mục 3 trang 77 SGK Toán 9 tập 1 - Kết nối tri thức trên giaitoan.edu.vn. Chúng tôi cung cấp lời giải đầy đủ, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập Toán 9.
Bài giải này được xây dựng bởi đội ngũ giáo viên giàu kinh nghiệm, đảm bảo tính chính xác và phù hợp với chương trình học.
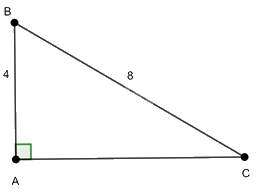
Cho tam giác vuông ABC có cạnh góc vuông AB = 4, cạnh huyền BC = 8. Tính cạnh AC (làm tròn đến số thập phân thứ ba) và các góc B, C (làm tròn đến độ).
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 3 trang 77 SGK Toán 9 Kết nối tri thức
Cho tam giác vuông ABC có cạnh góc vuông AB = 4, cạnh huyền BC = 8. Tính cạnh AC (làm tròn đến số thập phân thứ ba) và các góc B, C (làm tròn đến độ).
Phương pháp giải:
Từ định lý Pythagore ta tính được cạnh còn lại của tam giác ABC, và dựa vào tỉ số lượng giác của góc B và góc C, ta tính được góc B và góc C.
Lời giải chi tiết:
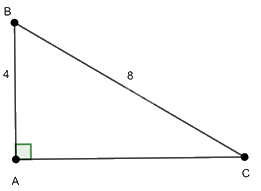
Tam giác ABC vuông tại A nên ta có: \(B{C^2} = {\rm{A}}{{\rm{B}}^2} + A{C^2}\) (Định lý Pythagore)
Thay số ta có: \({8^2} = {4^2} + A{C^2}\) hay \(A{C^2} = {8^2} - {4^2} = 48\) suy ra \(AC = \sqrt {48} = 4\sqrt 3 \approx 6,928 \)
Ta có: \(\cos \widehat B = \frac{{AB}}{{BC}} = \frac{4}{8} = \frac{1}{2}\) suy ra \(\widehat B = {60^0}\)
\(\sin \widehat C = \frac{{AB}}{{BC}} = \frac{4}{8} = \frac{1}{2}\) suy ra \(\widehat C = {30^0}\)
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 4 trang 77SGK Toán 9 Kết nối tri thức
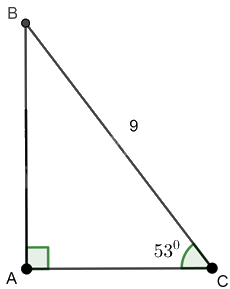
Giải tam giác ABC vuông tại A, biết \(BC = 9,\widehat C = {53^0}.\)
Phương pháp giải:
Giải tam giác vuông là tìm tất cả các cạnh và các góc chưa biết của tam giác vuông đó thông qua các tỉ số lượng giác hoặc định lý Pythagore.
Lời giải chi tiết:
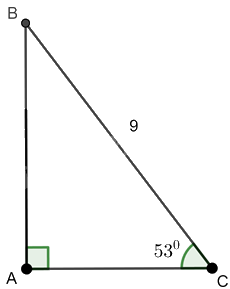
Tam giác ABC vuông tại A nên ta có: \(\cos \widehat C = \frac{{AC}}{{BC}}\) hay \(\cos {53^0} = \frac{{AC}}{9}\) suy ra \(AC = 9.\cos {53^0} \approx 5,42\)
\(\sin \widehat C = \frac{{AB}}{{BC}}\) hay \(\sin {53^0} = \frac{{AB}}{9}\) suy ra \(AB = 9.\sin {53^0} \approx 7,19\)
Ta có: \(\widehat A + \widehat B + \widehat C = {180^0}\) nên \({90^0} + \widehat B + {53^0} = {180^0}\) suy ra \(\widehat B = {37^0}.\)
Video hướng dẫn giải
Trả lời câu hỏi Câu hỏi trang 77SGK Toán 9 Kết nối tri thức
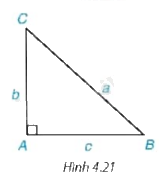
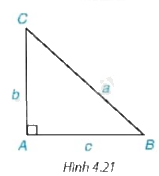
1. Hãy nêu cách giải tam giác ABC vuông tại A khi biết hai cạnh \(AB = c,AC = b\) hoặc \(AB = c,BC = a\) và không sử dụng định lý Pythagore (H.4.21).
2. Hãy nêu cách giải tam giác ABC vuông tại A khi biết cạnh góc vuông AB (hoặc cạnh huyền BC) và góc B.
Phương pháp giải:
Để giải tam giác vuông ngoài sử dụng định lý Pythagore ta có thể sử dụng tỉ số lượng giác.
Lời giải chi tiết:
1. Trường hợp biết \(AB = c,AC = b\)
Tam giác ABC vuông tại A nên ta có: \(\tan \widehat B = \frac{b}{c}\) từ đó ta tính được góc B, và tính được góc C thông qua định lý tổng ba góc trong một tam giác. Sau khi tính được góc B, ta dùng tỉ số lượng giác \(\cos \widehat B = \frac{c}{{CB}}\) từ đó ta tính được \(CB = \frac{c}{{\cos \widehat B}}\)
Trường hợp \(AB = c,BC = a\)
Tam giác ABC vuông tại A nên ta có: \(\cos \widehat B = \frac{b}{c}\) từ đó ta tính được góc B, và tính được góc C thông qua định lý tổng ba góc trong một tam giác. Sau khi tính được góc B, ta dùng tỉ số lượng giác \(\tan \widehat B = \frac{{AC}}{c}\) từ đó ta tính được \(AC = c.\tan \widehat B\)
2. Tam giác ABC vuông tại A khi biết cạnh góc vuông AB (hoặc cạnh huyền BC) và góc B.
Trường hợp biết cạnh góc vuông AB và góc B
Biết góc B ta tính được góc C thông qua định lý tổng ba góc trong một tam giác. Để tính cạnh BC ta dùng tỉ số lượng giác \(\cos \widehat B = \frac{c}{{BC}}\) từ đó ta tính được \(BC = \frac{c}{{\cos \widehat B}}\) và tỉ số lượng giác \(\tan \widehat B = \frac{{AC}}{c}\) từ đó ta tính được \(AC = c.\tan \widehat B\)
Trường hợp biết cạnh huyền BC và góc B
Biết góc B ta tính được góc C thông qua định lý tổng ba góc trong một tam giác. Để tính cạnh AB ta dùng tỉ số lượng giác \(\cos \widehat B = \frac{{AB}}{a}\) từ đó ta tính được \(AB = a.\cos \widehat B\) và tỉ số lượng giác \(\sin \widehat B = \frac{{AC}}{a}\) từ đó ta tính được \(AC = a.\sin \widehat B\)
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng trang 77 SGK Toán 9 Kết nối tri thức
Giải bài toán ở tình huống mở đầu với \(\alpha = {27^0},\beta = {19^0}.\)
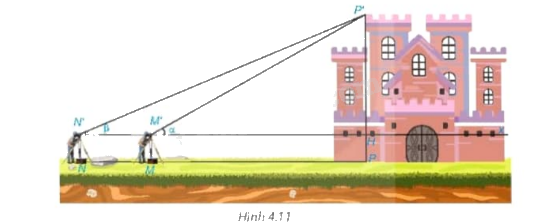
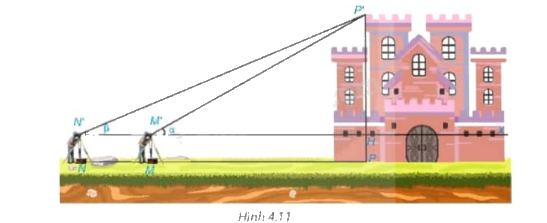
Tình huống mở đầu: Để đo chiều cao của một tòa lâu đài (H.4.11) , người ta đặt giác kế thẳng đứng tại M. Quay ống ngắm của giác kế sao cho nhìn thấy đỉnh P’ của tòa lâu đài dưới góc nhọn \(\alpha \). Sau đó, đặt giác kế thẳng đứng tại N, NM = 20 m, thì nhìn thấy đỉnh P’ dưới góc nhọn \(\beta \left( {\beta < \alpha } \right).\) Biết chiều cao giác kế là 1,6 m, hãy tính chiều cao của tòa lâu đài.
Phương pháp giải:
Ta thấy trong hình có hai tam giác vuông P’N’H và P’HM’ có cùng chiều cao từ đó ta tính được chiều cao của tam giác thông qua tỉ số lượng giác của góc \(\alpha ,\beta \) trong hai tam giác vuông và lập được phương trình. Chú ý để tính chiều cao của tòa lâu đài cần tính tổng chiều cao của giác kế và P’H. Độ dài đoạn MN bằng M’N’.
Lời giải chi tiết:
Ta có: \(\tan \alpha = \frac{{P'H}}{{M'H}}\) hay \(P'H = M'H.\tan {27^0}\)
\(\tan \beta = \frac{{P'H}}{{N'H}}\) hay \(P'H = N'H.\tan {19^0}\)
Từ đó ta có phương trình: \(M'H.\tan {27^0} = N'H.\tan {19^0}\)
hay \(M'H.\tan {27^0} = \left( {M'H + 20} \right).\tan {19^0}\)
suy ra \(M'H.\left( {\tan {{27}^0} - \tan {{19}^0}} \right) = 20.\tan {19^0}\)
nên \(M'H = \frac{{20.\tan {{19}^0}}}{{{\tan {{27}^0} - \tan {{19}^0}} }} \approx 41,69\) m
\(P'H = M'H.\tan {27^0} \approx 21,24\) m
Chiều cao của tòa lâu đài khoảng: \(21,24 + 1,6 = 22,84\) m.
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 3 trang 77 SGK Toán 9 Kết nối tri thức
Cho tam giác vuông ABC có cạnh góc vuông AB = 4, cạnh huyền BC = 8. Tính cạnh AC (làm tròn đến số thập phân thứ ba) và các góc B, C (làm tròn đến độ).
Phương pháp giải:
Từ định lý Pythagore ta tính được cạnh còn lại của tam giác ABC, và dựa vào tỉ số lượng giác của góc B và góc C, ta tính được góc B và góc C.
Lời giải chi tiết:
Tam giác ABC vuông tại A nên ta có: \(B{C^2} = {\rm{A}}{{\rm{B}}^2} + A{C^2}\) (Định lý Pythagore)
Thay số ta có: \({8^2} = {4^2} + A{C^2}\) hay \(A{C^2} = {8^2} - {4^2} = 48\) suy ra \(AC = \sqrt {48} = 4\sqrt 3 \approx 6,928 \)
Ta có: \(\cos \widehat B = \frac{{AB}}{{BC}} = \frac{4}{8} = \frac{1}{2}\) suy ra \(\widehat B = {60^0}\)
\(\sin \widehat C = \frac{{AB}}{{BC}} = \frac{4}{8} = \frac{1}{2}\) suy ra \(\widehat C = {30^0}\)
Video hướng dẫn giải
Trả lời câu hỏi Câu hỏi trang 77SGK Toán 9 Kết nối tri thức
1. Hãy nêu cách giải tam giác ABC vuông tại A khi biết hai cạnh \(AB = c,AC = b\) hoặc \(AB = c,BC = a\) và không sử dụng định lý Pythagore (H.4.21).
2. Hãy nêu cách giải tam giác ABC vuông tại A khi biết cạnh góc vuông AB (hoặc cạnh huyền BC) và góc B.
Phương pháp giải:
Để giải tam giác vuông ngoài sử dụng định lý Pythagore ta có thể sử dụng tỉ số lượng giác.
Lời giải chi tiết:
1. Trường hợp biết \(AB = c,AC = b\)
Tam giác ABC vuông tại A nên ta có: \(\tan \widehat B = \frac{b}{c}\) từ đó ta tính được góc B, và tính được góc C thông qua định lý tổng ba góc trong một tam giác. Sau khi tính được góc B, ta dùng tỉ số lượng giác \(\cos \widehat B = \frac{c}{{CB}}\) từ đó ta tính được \(CB = \frac{c}{{\cos \widehat B}}\)
Trường hợp \(AB = c,BC = a\)
Tam giác ABC vuông tại A nên ta có: \(\cos \widehat B = \frac{b}{c}\) từ đó ta tính được góc B, và tính được góc C thông qua định lý tổng ba góc trong một tam giác. Sau khi tính được góc B, ta dùng tỉ số lượng giác \(\tan \widehat B = \frac{{AC}}{c}\) từ đó ta tính được \(AC = c.\tan \widehat B\)
2. Tam giác ABC vuông tại A khi biết cạnh góc vuông AB (hoặc cạnh huyền BC) và góc B.
Trường hợp biết cạnh góc vuông AB và góc B
Biết góc B ta tính được góc C thông qua định lý tổng ba góc trong một tam giác. Để tính cạnh BC ta dùng tỉ số lượng giác \(\cos \widehat B = \frac{c}{{BC}}\) từ đó ta tính được \(BC = \frac{c}{{\cos \widehat B}}\) và tỉ số lượng giác \(\tan \widehat B = \frac{{AC}}{c}\) từ đó ta tính được \(AC = c.\tan \widehat B\)
Trường hợp biết cạnh huyền BC và góc B
Biết góc B ta tính được góc C thông qua định lý tổng ba góc trong một tam giác. Để tính cạnh AB ta dùng tỉ số lượng giác \(\cos \widehat B = \frac{{AB}}{a}\) từ đó ta tính được \(AB = a.\cos \widehat B\) và tỉ số lượng giác \(\sin \widehat B = \frac{{AC}}{a}\) từ đó ta tính được \(AC = a.\sin \widehat B\)
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 4 trang 77SGK Toán 9 Kết nối tri thức
Giải tam giác ABC vuông tại A, biết \(BC = 9,\widehat C = {53^0}.\)
Phương pháp giải:
Giải tam giác vuông là tìm tất cả các cạnh và các góc chưa biết của tam giác vuông đó thông qua các tỉ số lượng giác hoặc định lý Pythagore.
Lời giải chi tiết:
Tam giác ABC vuông tại A nên ta có: \(\cos \widehat C = \frac{{AC}}{{BC}}\) hay \(\cos {53^0} = \frac{{AC}}{9}\) suy ra \(AC = 9.\cos {53^0} \approx 5,42\)
\(\sin \widehat C = \frac{{AB}}{{BC}}\) hay \(\sin {53^0} = \frac{{AB}}{9}\) suy ra \(AB = 9.\sin {53^0} \approx 7,19\)
Ta có: \(\widehat A + \widehat B + \widehat C = {180^0}\) nên \({90^0} + \widehat B + {53^0} = {180^0}\) suy ra \(\widehat B = {37^0}.\)
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng trang 77 SGK Toán 9 Kết nối tri thức
Giải bài toán ở tình huống mở đầu với \(\alpha = {27^0},\beta = {19^0}.\)
Tình huống mở đầu: Để đo chiều cao của một tòa lâu đài (H.4.11) , người ta đặt giác kế thẳng đứng tại M. Quay ống ngắm của giác kế sao cho nhìn thấy đỉnh P’ của tòa lâu đài dưới góc nhọn \(\alpha \). Sau đó, đặt giác kế thẳng đứng tại N, NM = 20 m, thì nhìn thấy đỉnh P’ dưới góc nhọn \(\beta \left( {\beta < \alpha } \right).\) Biết chiều cao giác kế là 1,6 m, hãy tính chiều cao của tòa lâu đài.
Phương pháp giải:
Ta thấy trong hình có hai tam giác vuông P’N’H và P’HM’ có cùng chiều cao từ đó ta tính được chiều cao của tam giác thông qua tỉ số lượng giác của góc \(\alpha ,\beta \) trong hai tam giác vuông và lập được phương trình. Chú ý để tính chiều cao của tòa lâu đài cần tính tổng chiều cao của giác kế và P’H. Độ dài đoạn MN bằng M’N’.
Lời giải chi tiết:
Ta có: \(\tan \alpha = \frac{{P'H}}{{M'H}}\) hay \(P'H = M'H.\tan {27^0}\)
\(\tan \beta = \frac{{P'H}}{{N'H}}\) hay \(P'H = N'H.\tan {19^0}\)
Từ đó ta có phương trình: \(M'H.\tan {27^0} = N'H.\tan {19^0}\)
hay \(M'H.\tan {27^0} = \left( {M'H + 20} \right).\tan {19^0}\)
suy ra \(M'H.\left( {\tan {{27}^0} - \tan {{19}^0}} \right) = 20.\tan {19^0}\)
nên \(M'H = \frac{{20.\tan {{19}^0}}}{{{\tan {{27}^0} - \tan {{19}^0}} }} \approx 41,69\) m
\(P'H = M'H.\tan {27^0} \approx 21,24\) m
Chiều cao của tòa lâu đài khoảng: \(21,24 + 1,6 = 22,84\) m.
Mục 3 trang 77 SGK Toán 9 tập 1 - Kết nối tri thức tập trung vào việc vận dụng các kiến thức về hàm số bậc nhất và hàm số bậc hai đã học để giải quyết các bài toán thực tế. Các bài tập trong mục này thường yêu cầu học sinh xác định hệ số góc, điểm thuộc đồ thị, tìm giao điểm của hai đường thẳng, và giải các bài toán liên quan đến ứng dụng của hàm số.
Mục 3 bao gồm một số bài tập với mức độ khó tăng dần. Bài tập đầu tiên thường là các bài tập cơ bản về việc xác định các yếu tố của hàm số. Các bài tập tiếp theo yêu cầu học sinh phải vận dụng linh hoạt các kiến thức đã học để giải quyết các bài toán phức tạp hơn.
Bài tập này yêu cầu học sinh xác định hệ số góc của đường thẳng và kiểm tra xem một điểm cho trước có thuộc đồ thị của hàm số hay không. Để giải bài tập này, học sinh cần nắm vững định nghĩa của hệ số góc và phương trình đường thẳng.
Bài tập này yêu cầu học sinh tìm tọa độ giao điểm của hai đường thẳng. Để giải bài tập này, học sinh cần giải hệ phương trình bậc nhất hai ẩn tương ứng với hai đường thẳng.
Bài tập này yêu cầu học sinh giải các bài toán thực tế liên quan đến ứng dụng của hàm số. Ví dụ, bài toán về việc tính quãng đường đi được của một vật chuyển động đều, hoặc bài toán về việc tính giá tiền của một sản phẩm khi mua với số lượng khác nhau.
Để giải tốt các bài tập trong Mục 3, học sinh cần nắm vững các kiến thức sau:
Ngoài ra, học sinh cũng cần luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau và rèn luyện kỹ năng giải toán.
Dưới đây là lời giải chi tiết của từng bài tập trong Mục 3 trang 77 SGK Toán 9 tập 1 - Kết nối tri thức:
...
...
...
Khi giải bài tập, học sinh cần chú ý các điểm sau:
Mục 3 trang 77 SGK Toán 9 tập 1 - Kết nối tri thức là một phần quan trọng trong chương trình học Toán 9. Việc nắm vững kiến thức và kỹ năng giải các bài tập trong mục này sẽ giúp học sinh tự tin hơn khi làm bài kiểm tra và thi cử. Chúc các em học tốt!
Giả sử ta có hàm số y = 2x + 1. Để xác định xem điểm A(1; 3) có thuộc đồ thị của hàm số hay không, ta thay x = 1 vào phương trình hàm số và kiểm tra xem y có bằng 3 hay không. Nếu y = 3, thì điểm A thuộc đồ thị của hàm số. Ngược lại, nếu y khác 3, thì điểm A không thuộc đồ thị của hàm số.
| Khái niệm | Định nghĩa |
|---|---|
| Hàm số bậc nhất | Hàm số có dạng y = ax + b, trong đó a và b là các số thực. |
| Hệ số góc | Số a trong phương trình hàm số bậc nhất y = ax + b. |