Bài tập 10.6 trang 100 SGK Toán 9 tập 2 thuộc chương trình Toán 9 Kết nối tri thức, yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế. Bài viết này sẽ cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Giaitoan.edu.vn luôn đồng hành cùng các em học sinh trong quá trình học tập, cung cấp các tài liệu học tập chất lượng, đáp án chính xác và phương pháp giải bài tập hiệu quả.
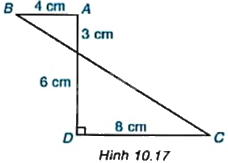
Tính thể tích của hình tạo thành khi cho hình ABCD quanh AD một vòng (H.10.17).
Đề bài
Tính thể tích của hình tạo thành khi cho hình ABCD quanh AD một vòng (H.10.17).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Khi quay hình ABCD quanh cạnh AD một vòng thì ta được một hình gồm hai hình nón có:
+ Hình nón thứ nhất có chiều cao bằng 3cm, bán kính đáy bằng 4cm.
+ Hình nón thứ hai có chiều cao bằng 6cm, bán kính đáy bằng 8cm.
Thể tích của hình nón bán kính r và chiều cao h là: \(V = \frac{1}{3}\pi {r^2}h\).
Lời giải chi tiết
Khi quay hình ABCD quanh cạnh AD một vòng thì ta được một hình gồm hai hình nón có:
+ Hình nón thứ nhất có chiều cao bằng 3cm, bán kính đáy bằng 4cm.
+ Hình nón thứ hai có chiều cao bằng 6cm, bán kính đáy bằng 8cm.
Thể tích hình nón thứ nhất là: \({V_1} = \frac{1}{3}\pi {.4^2}.3 = 16\pi \left( {c{m^3}} \right)\).
Thể tích hình nón thứ hai là: \({V_2} = \frac{1}{3}\pi {.8^2}.6 = 128\pi \left( {c{m^3}} \right)\).
Thể tích hình cần tìm là: \(V = {V_1} + {V_2} = 16\pi + 128\pi = 144\pi \left( {c{m^3}} \right)\).
Bài tập 10.6 trang 100 SGK Toán 9 tập 2 yêu cầu học sinh giải quyết một bài toán thực tế liên quan đến hàm số bậc hai. Để giải bài tập này, chúng ta cần nắm vững các kiến thức sau:
Bài toán 10.6 thường mô tả một tình huống thực tế, ví dụ như việc xác định quỹ đạo của một vật được ném lên, hoặc tìm kích thước tối ưu của một hình chữ nhật để có diện tích lớn nhất. Để giải bài toán này, chúng ta cần:
Giả sử bài toán yêu cầu tìm giá trị lớn nhất của hàm số y = -x2 + 4x - 1. Chúng ta sẽ thực hiện các bước sau:
Để giải bài tập 10.6 trang 100 SGK Toán 9 tập 2 một cách hiệu quả, các em học sinh cần:
Để củng cố kiến thức và kỹ năng giải bài tập về hàm số bậc hai, các em học sinh có thể luyện tập thêm các bài tập tương tự trong SGK Toán 9 tập 2 và các tài liệu tham khảo khác. Một số bài tập gợi ý:
Bài tập 10.6 trang 100 SGK Toán 9 tập 2 là một bài tập quan trọng giúp học sinh hiểu sâu hơn về hàm số bậc hai và ứng dụng của nó trong thực tế. Hy vọng với hướng dẫn chi tiết và ví dụ minh họa trong bài viết này, các em học sinh sẽ tự tin giải quyết bài tập và đạt kết quả tốt trong môn Toán.