Bài tập 9.36 trang 91 SGK Toán 9 tập 2 thuộc chương trình Toán 9 Kết nối tri thức, yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế. Bài viết này sẽ cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Giaitoan.edu.vn luôn đồng hành cùng các em học sinh trên con đường chinh phục môn Toán. Chúng tôi cung cấp đầy đủ các bài giải SGK Toán 9, bài tập trắc nghiệm, và các tài liệu học tập hữu ích khác.
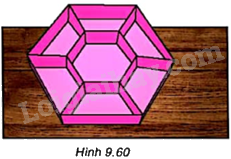
Người ta muốn làm một khay đựng bánh kẹo hình lục giác đều có cạnh 10cm và chia thành 7 ngăn gồm một lục giác đều nhỏ và 6 hình thang cân như Hình 9.60. Hỏi lục giác đều nhỏ phải có cạnh bằng bao nhiêu để nó có diện tích bằng hai lần diện tích mỗi hình thang?
Đề bài
Người ta muốn làm một khay đựng bánh kẹo hình lục giác đều có cạnh 10cm và chia thành 7 ngăn gồm một lục giác đều nhỏ và 6 hình thang cân như Hình 9.60. Hỏi lục giác đều nhỏ phải có cạnh bằng bao nhiêu để nó có diện tích bằng hai lần diện tích mỗi hình thang?
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Gọi O là tâm đa giác lớn và đa giác nhỏ.
- Dựa vào kiến thức về lục giác đều, ta có hình lục giác được chia thành 6 tam giác đều chung đỉnh O, 2 đỉnh còn lại là các đỉnh 2 đỉnh kề nhau của lục giác.
- Lấy hai điểm A, B là hai đỉnh kề nhau của lục giác nhỏ như hình vẽ. Đặt AB = x (cm). Khi đó ta có \(\Delta AOB\) đều.
- Kẻ \(OH \bot AB\), tính đường cao OH của tam giác AOB. Từ đó ta tính được \({S_{\Delta AOB}}\).
Từ đó ta tính được diện tích hình lục giác đều nhỏ: Slục giácđều nhỏ \( = 6.{S_{\Delta AOB}}\).
Vì diện tích lục giác đều nhỏ bằng hai lần diện tích mỗi hình thang nên diện tích mỗi hình thang là:
Shình thang = Slục giácđều nhỏ : 2, suy ra tổng diện tích 6 hình thang.
Ta tính được Slục giác đều lớn = Slục giácđều nhỏ + S6 hình thang.
Mà ta còn tính được diện tích hình lục giác đều lớn qua cạnh của nó giống như Slục giácđều nhỏ.
Từ đó giải phương trình để tìm x.
Lời giải chi tiết
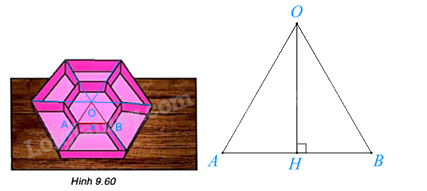
Nối các cặp đỉnh đối diện của lục giác với nhau, ta được điểm O là tâm của hình lục giác lớn và lục giác nhỏ.
Ta chia hình lục giác thành 6 tam giác đều chung đỉnh O, 2 đỉnh còn lại là các đỉnh 2 đỉnh kề nhau của lục giác.
Lấy hai điểm A, B là hai đỉnh kề nhau của lục giác nhỏ như hình vẽ. Đặt AB = x (cm) \(\left( {0 < x < 10} \right)\).
Khi đó \(\Delta AOB\) đều có \(OA = OB = AB = x\) và \(\widehat B = 60^\circ \).
Kẻ \(OH \bot AB\). Dựa vào hệ thức giữa cạnh và góc trong tam giác vuông, ta có:
\(OH = OB.\sin \widehat {OBA} = x.\sin 60^\circ = \frac{{\sqrt 3 }}{2}x\left( {cm} \right)\)
Suy ra \({S_{\Delta AOB}} = \frac{{OH.AB}}{2} = \frac{{\frac{{\sqrt 3 }}{2}x.x}}{2} = \frac{{{x^2}\sqrt 3 }}{4}\left( {c{m^2}} \right)\)
Ta có diện tích hình lục giác đều nhỏ là:
Slục giácđều nhỏ \( = 6.{S_{\Delta AOB}} = 6.\frac{{{x^2}\sqrt 3 }}{4} = \frac{{3\sqrt 3 {x^2}}}{2}\left( {c{m^2}} \right)\).
Theo đề bài, diện tích lục giác đều nhỏ bằng hai lần diện tích mỗi hình thang nên diện tích mỗi hình thang là:
Shình thang = Slục giácđều nhỏ : 2 = \(\frac{{3\sqrt 3 {x^2}}}{2}:2 = \frac{{3\sqrt 3 {x^2}}}{4}\left( {c{m^2}} \right)\),
suy ra tổng diện tích 6 hình thang là: \(6.\frac{{3\sqrt 3 {x^2}}}{4} = \frac{{9\sqrt 3 {x^2}}}{2}\left( {c{m^2}} \right)\)
Do đó, diện tích lục giác đều lớn là:
Slục giác đều lớn = Slục giácđều nhỏ + S6 hình thang \( = \frac{{3\sqrt 3 {x^2}}}{2} + \frac{{9\sqrt 3 {x^2}}}{2} = \frac{{12\sqrt 3 {x^2}}}{2} = 6\sqrt 3 {x^2}\left( {c{m^2}} \right)\) (1)
Mà tương tự như Slục giácđều nhỏ, ta cũng có thể tính được diện tích lục giác đều theo độ dài cạnh của nó theo công thức \(S = \frac{{3\sqrt 3 {x^2}}}{2}\left( {c{m^2}} \right)\) với x là độ dài cạnh.
Suy ra Slục giác đều lớn \( = \frac{{3\sqrt 3 {{.10}^2}}}{2} = 150\sqrt 3 \left( {c{m^2}} \right)\) (2)
Từ (1) và (2), ta có phương trình: \(6\sqrt 3 {x^2} = 150\sqrt 3 \)
suy ra \({x^2} = 25\), do đó \(x = 5\)(thỏa mãn vi \(0 < x < 10\)).
Vậy cạnh của lục giác đều nhỏ là 5cm.
Bài tập 9.36 trang 91 SGK Toán 9 tập 2 yêu cầu học sinh giải một bài toán thực tế liên quan đến hàm số bậc hai. Để giải bài tập này, chúng ta cần xác định được hàm số bậc hai phù hợp với dữ kiện đề bài, sau đó tìm các hệ số của hàm số và giải các phương trình tương ứng.
Trước khi bắt đầu giải bài tập, chúng ta cần đọc kỹ đề bài và phân tích các thông tin được cung cấp. Từ đó, xác định được các yếu tố quan trọng như các điểm mà đồ thị hàm số đi qua, trục đối xứng của đồ thị, hoặc đỉnh của đồ thị. Dựa vào các yếu tố này, chúng ta có thể xác định được dạng tổng quát của hàm số bậc hai: y = ax2 + bx + c.
Sau khi xác định được dạng tổng quát của hàm số, chúng ta cần tìm các hệ số a, b, c. Để làm điều này, chúng ta có thể sử dụng các điểm mà đồ thị hàm số đi qua. Thay tọa độ của các điểm này vào phương trình hàm số, chúng ta sẽ có một hệ phương trình bậc hai với ba ẩn a, b, c. Giải hệ phương trình này, chúng ta sẽ tìm được giá trị của các hệ số a, b, c.
Sau khi tìm được các hệ số a, b, c, chúng ta có thể viết được phương trình hàm số bậc hai cụ thể. Dựa vào phương trình này, chúng ta có thể giải các phương trình tương ứng để tìm ra các giá trị cần thiết của bài toán. Ví dụ, chúng ta có thể tìm ra nghiệm của phương trình bậc hai, hoặc tìm ra tọa độ của đỉnh của đồ thị hàm số.
Giả sử đề bài cho biết đồ thị hàm số đi qua các điểm A(0; 1), B(1; 2), và C(-1; 0). Chúng ta có thể thay tọa độ của các điểm này vào phương trình y = ax2 + bx + c để có được hệ phương trình sau:
Giải hệ phương trình này, chúng ta sẽ tìm được a = 1, b = 1, và c = 1. Vậy phương trình hàm số là y = x2 + x + 1.
Khi giải bài tập về hàm số bậc hai, các em học sinh cần lưu ý một số điều sau:
Để củng cố kiến thức về hàm số bậc hai, các em học sinh có thể làm thêm một số bài tập tương tự. Dưới đây là một số bài tập gợi ý:
Bài tập 9.36 trang 91 SGK Toán 9 tập 2 là một bài tập quan trọng giúp các em học sinh hiểu sâu hơn về hàm số bậc hai và ứng dụng của nó trong giải quyết các bài toán thực tế. Hy vọng rằng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán.