Bài tập 9.16 trang 79 SGK Toán 9 tập 2 thuộc chương trình Kết nối tri thức là một bài toán quan trọng giúp học sinh rèn luyện kỹ năng về hàm số bậc hai. Bài tập này thường yêu cầu học sinh xác định hệ số a, b, c của hàm số, tìm đỉnh của parabol, và vẽ đồ thị hàm số.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 9.16 trang 79 SGK Toán 9 tập 2, giúp các em học sinh hiểu rõ phương pháp giải và áp dụng vào các bài tập tương tự.
Trong một khu vui chơi có dạng hình tam giác đều có cạnh bằng 60m, người ta muốn tìm một vị trí đặt bộ phát sóng wifi sao cho ở chỗ nào trong khu vui chơi đó đều có thể bắt được sóng. Biết rằng bộ phát sóng đó có tầm phát sóng tối đa 50m, hỏi rằng có thể tìm được vị trí để đặt bộ phát sóng như vậy hay không?
Đề bài
Trong một khu vui chơi có dạng hình tam giác đều có cạnh bằng 60m, người ta muốn tìm một vị trí đặt bộ phát sóng wifi sao cho ở chỗ nào trong khu vui chơi đó đều có thể bắt được sóng. Biết rằng bộ phát sóng đó có tầm phát sóng tối đa 50m, hỏi rằng có thể tìm được vị trí để đặt bộ phát sóng như vậy hay không?
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+Để vị trí của bộ phát sóng wifi sao cho ở chỗ nào trong khu vui chơi đó đều có thể bắt được sóng thì bộ phát sóng wifi đặt ở tâm đường tròn ngoại tiếp tam giác khu vui chơi đó.
+ Đường tròn ngoại tiếp tam giác đều cạnh a có tâm là trọng tâm của tam giác đó và bán kính bằng \(\frac{{\sqrt 3 }}{3}a\).
+ So sánh OA với 50m để đưa ra kết luận.
Lời giải chi tiết
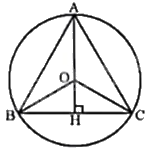
Để vị trí của bộ phát sóng wifi sao cho ở chỗ nào trong khu vui chơi đó đều có thể bắt được sóng thì bộ phát sóng wifi đặt ở tâm đường tròn ngoài tiếp tam giác khu vui chơi đó
Xét khu vui chơi hình tam giác đều là tam giác ABC có cạnh 60m. Xét đường tròn tâm (O) ngoại tiếp tam giác ABC đó.
Vẽ đường cao AH của tam giác ABC. Tam giác ABC đều nên AH vừa là đường trung trực, vừa là đường trung tuyến của tam giác.
Bán kính đường tròn ngoại tiếp \(\Delta \)ABC là:
\(OA = \frac{{BC\sqrt 3 }}{3} = \frac{{60\sqrt 3 }}{3} = 20\sqrt 3 \left( m \right)\).
Vì \(20\sqrt 3 m \approx 34,64m < 50m\) nên bộ phát sóng đó đặt ở tâm đường tròn ngoại tiếp tam giác thì cả khu vui chơi đều có thể bắt sóng được.
Bài tập 9.16 SGK Toán 9 tập 2 Kết nối tri thức yêu cầu học sinh xét hàm số y = x2 - 4x + 3. Chúng ta sẽ cùng nhau phân tích và giải quyết bài toán này một cách chi tiết và dễ hiểu.
Hàm số y = x2 - 4x + 3 là một hàm số bậc hai có dạng y = ax2 + bx + c, với:
Vì a = 1 > 0, hàm số có đồ thị là một parabol hướng lên trên.
Tọa độ đỉnh của parabol có dạng I(x0; y0), trong đó:
Vậy, tọa độ đỉnh của parabol là I(2; -1).
Trục đối xứng của parabol là đường thẳng x = x0, tức là x = 2.
Để tìm giao điểm của parabol với trục hoành, ta giải phương trình y = 0:
x2 - 4x + 3 = 0
Phương trình này có hai nghiệm phân biệt:
Vậy, parabol cắt trục hoành tại hai điểm A(1; 0) và B(3; 0).
Để tìm giao điểm của parabol với trục tung, ta cho x = 0:
y = 02 - 4 * 0 + 3 = 3
Vậy, parabol cắt trục tung tại điểm C(0; 3).
Dựa vào các yếu tố đã tìm được, ta có thể vẽ đồ thị hàm số y = x2 - 4x + 3:
Đồ thị hàm số là một parabol hướng lên trên, có đỉnh tại I(2; -1), cắt trục hoành tại A(1; 0) và B(3; 0), và cắt trục tung tại C(0; 3).
Thông qua việc giải bài tập 9.16 trang 79 SGK Toán 9 tập 2 Kết nối tri thức, chúng ta đã nắm vững các bước để xác định các yếu tố của hàm số bậc hai và vẽ đồ thị hàm số. Việc hiểu rõ các yếu tố này sẽ giúp các em giải quyết các bài toán liên quan đến hàm số bậc hai một cách dễ dàng và hiệu quả hơn.
Hy vọng bài giải chi tiết này sẽ giúp các em học sinh hiểu rõ hơn về bài tập 9.16 và các kiến thức liên quan đến hàm số bậc hai. Chúc các em học tập tốt!
| Yếu tố | Giá trị |
|---|---|
| a | 1 |
| b | -4 |
| c | 3 |
| Đỉnh I | (2; -1) |
| Trục đối xứng | x = 2 |
| Bảng tóm tắt các yếu tố của hàm số | |