Bài tập 4.12 trang 78 SGK Toán 9 tập 1 thuộc chương Hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế. Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cập nhật lời giải các bài tập Toán 9 tập 1 mới nhất, đảm bảo tính chính xác và đầy đủ.
Cho hình thang ABCD (AD // BC) có (AD = 16cm,BC = 4cm,widehat A = widehat B = widehat {ACD} = {90^0}.) a) Kẻ đường cao CE của tam giác ACD. Chứng minh (widehat {ADC} = widehat {ACE}.) Tính sin của các góc (widehat {ADC},widehat {ACE}) và suy ra (A{C^2} = AE.AD.) Từ đó tính AC. b) Tính góc D của hình thang.
Đề bài
Cho hình thang ABCD (AD // BC) có \(AD = 16cm,BC = 4cm,\widehat A = \widehat B = \widehat {ACD} = {90^0}.\)
a) Kẻ đường cao CE của tam giác ACD. Chứng minh \(\widehat {ADC} = \widehat {ACE}.\) Tính sin của các góc \(\widehat {ADC},\widehat {ACE}\) và suy ra \(A{C^2} = AE.AD.\) Từ đó tính AC.
b) Tính góc D của hình thang.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Từ hai góc bằng nhau nên ta có tỉ số lượng giác của hai góc gần như nhau. Từ đó ta lập được tỉ lệ của hai góc này. Rồi tính AC, góc D
Lời giải chi tiết
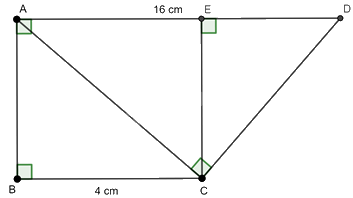
a) Xét tam giác CDE vuông tại E có:
\(\widehat {DCE} + \widehat {ADC} = 90^\circ\)
Theo bài ra ta có: \(\widehat {ACD} = 90^\circ\) nên \(\widehat {DCE} + \widehat {ACE}= 90^\circ\)
Suy ra \(\widehat {ADC} = \widehat {ACE}\) (cùng phụ với góc DCE)
Ta có \(\sin \widehat {ADC} = \frac{{AC}}{{AD}};\sin \widehat {ACE} = \frac{{AE}}{{AC}}.\)
Từ đó ta có \(\frac{{AC}}{{AD}} = \frac{{AE}}{{AC}}\) hay \(A{C^2} = AE.AD.\)
AECB là hình chữ nhật do \(\widehat {BAE} = \widehat {ABC} = \widehat {AEC} = {90^0}\) do đó ta có \(AE = BC = 4\) cm.
Nên \(A{C^2} = AE.AD = 4.16 = 64\) hay \(AC = \sqrt {64} = 8\) cm (vì \(AC > 0\))
b) \(\sin \widehat {ADC} = \frac{{AC}}{{AD}}\) hay \(\sin \widehat {ADC} = \frac{8}{{16}} = \frac{1}{2}\) hay \(\sin \widehat {ADC} = {30^0}\)
Bài tập 4.12 trang 78 SGK Toán 9 tập 1 - Kết nối tri thức là một bài toán ứng dụng thực tế về hàm số bậc nhất. Để giải bài tập này, học sinh cần nắm vững các kiến thức sau:
Đề bài: (Đề bài cụ thể của bài tập 4.12 sẽ được trình bày chi tiết ở đây)
Lời giải:
Ví dụ minh họa: (Ví dụ cụ thể về cách giải bài tập 4.12, bao gồm các bước giải chi tiết và giải thích rõ ràng)
Lưu ý:
Ngoài bài tập 4.12, các em học sinh có thể tham khảo thêm các bài tập khác trong SGK Toán 9 tập 1 - Kết nối tri thức để củng cố kiến thức về hàm số bậc nhất. Các em cũng có thể tìm hiểu thêm về các ứng dụng của hàm số bậc nhất trong thực tế, ví dụ như trong lĩnh vực kinh tế, kỹ thuật, khoa học,...
Để luyện tập thêm, các em có thể thử giải các bài tập sau:
Giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và dễ hiểu này, các em học sinh sẽ nắm vững kiến thức và tự tin giải quyết các bài tập về hàm số bậc nhất. Chúc các em học tập tốt!
Các khái niệm liên quan:
Các dạng bài tập thường gặp: