Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 3, trang 13, 14 và 15 của sách giáo khoa Toán 9 tập 2 - Kết nối tri thức.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Thực hiện các bước sau để giải phương trình: (2{x^2} - 8x + 3 = 0). a) Chuyển hạng tử tự do sang vế phải. b) Chia cả hai vế của phương trình cho hệ số của ({x^2}). c) Thêm vào hai vế của phương trình nhận được ở câu b với cùng một số để vế trái có thể biến đổi thành một bình phương. Từ đó tìm nghiệm x.
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 5 trang 14SGK Toán 9 Kết nối tri thức
Áp dụng công thức nghiệm, giải các phương trình sau:
a) \(2{x^2} - 5x + 1 = 0\);
b) \({x^2} + 8x + 16 = 0\);
c) \({x^2} - x + 1 = 0\).
Phương pháp giải:
Xét phương trình bậc hai một ẩn \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\). Tính biệt thức \(\Delta = {b^2} - 4ac\).
+ Nếu \(\Delta > 0\) thì phương trình có hai nghiệm phân biệt: \({x_1} = \frac{{ - b + \sqrt \Delta }}{{2a}};{x_2} = \frac{{ - b - \sqrt \Delta }}{{2a}}\).
+ Nếu \(\Delta = 0\) thì phương trình có nghiệm kép: \({x_1} = {x_2} = \frac{{ - b}}{{2a}}\).
+ Nếu \(\Delta < 0\) thì phương trình vô nghiệm.
Lời giải chi tiết:
a) Ta có: \(\Delta = {\left( { - 5} \right)^2} - 4.2.1 = 17 > 0\) nên phương trình có hai nghiệm phân biệt \({x_1} = \frac{{5 + \sqrt {17} }}{4};{x_2} = \frac{{5 - \sqrt {17} }}{4}\)
b) Ta có: \(\Delta = {8^2} - 4.1.16 = 0\) nên phương trình có nghiệm kép:\({x_1} = {x_2} = \frac{{ - 8}}{2} = - 4\)
c) Ta có: \(\Delta = {\left( { - 1} \right)^2} - 4.1.1 = - 3 < 0\) nên phương trình vô nghiệm.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 4 trang 13 SGK Toán 9 Kết nối tri thức
Thực hiện các bước sau để giải phương trình: \(2{x^2} - 8x + 3 = 0\).
a) Chuyển hạng tử tự do sang vế phải.
b) Chia cả hai vế của phương trình cho hệ số của \({x^2}\).
c) Thêm vào hai vế của phương trình nhận được ở câu b với cùng một số để vế trái có thể biến đổi thành một bình phương. Từ đó tìm nghiệm x.
Phương pháp giải:
a) Chuyển hạng tử tự do của phương trình sang vế phải ta được phương trình \(2{x^2} - 8x = - 3\).
b) Chia cả hai vế của phương trình cho hệ số của \({x^2}\) ta được: \({x^2} - 4x = \frac{{ - 3}}{2}\).
c) Các bước giải phương trình:
+ Bước 1: Cộng thêm 4 vào 2 vế để đưa phương trình về dạng: \({A^2} = B\left( {B \ge 0} \right)\).
+ Bước 2: Nếu \({A^2} = B\left( {B \ge 0} \right)\) thì \(A = \sqrt B \) hoặc \(A = - \sqrt B \). Giải các phương trình đó và kết luận.
Lời giải chi tiết:
a) Chuyển hạng tử tự do của phương trình sang vế phải ta được phương trình \(2{x^2} - 8x = - 3\).
b) Chia cả hai vế của phương trình cho hệ số của \({x^2}\) ta được: \({x^2} - 4x = \frac{{ - 3}}{2}\).
c) \({x^2} - 4x = \frac{{ - 3}}{2}\)
\({x^2} - 4x + 4 = \frac{{ - 3}}{2} + 4\)
\({\left( {x - 2} \right)^2} = \frac{5}{2}\)
\(x - 2 = \frac{{\sqrt {10} }}{2}\) hoặc \(x - 2 = - \frac{{\sqrt {10} }}{2}\)
\(x = 2 + \frac{{\sqrt {10} }}{2}\) \(x = 2 - \frac{{\sqrt {10} }}{2}\)
Vậy phương trình có hai nghiệm \(x = 2 + \frac{{\sqrt {10} }}{2}\); \(x = 2 - \frac{{\sqrt {10} }}{2}\).
Video hướng dẫn giải
Trả lời câu hỏi Thử thách nhỏ trang 14 SGK Toán 9 Kết nối tri thức
Pi hỏi: Có thể nói gì về nghiệm của phương trình bậc hai \(a{x^2} + bx + c = 0\) nếu a và c trái dấu?
Em hãy trả lời câu hỏi của anh Pi.
Phương pháp giải:
Xét phương trình bậc hai một ẩn \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có: \(\Delta = {b^2} - 4ac\)
Nếu a và c trái dấu thì tích \(ac < 0\). Từ đó, xét dấu của biệt thức \(\Delta \). Do đó, kết luận được số nghiệm của phương trình \(a{x^2} + bx + c = 0\).
Lời giải chi tiết:
Vì a và c trái dấu thì tích \(ac < 0\), suy ra: \( - ac > 0\).
Do đó, \(\Delta = {b^2} - 4ac > 0\). Suy ra, phương trình \(a{x^2} + bx + c = 0\) có hai nghiệm phân biệt.
Vậy nếu a và c trái dấu thì phương trình bậc hai \(a{x^2} + bx + c = 0\) có hai nghiệm phân biệt.
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 6 trang 15 SGK Toán 9 Kết nối tri thức
Xác định a, b’, c rồi dùng công thức nghiệm thu gọn giải các phương trình sau:
a) \(3{x^2} + 8x - 3 = 0\);
b) \({x^2} + 6\sqrt 2 x + 2 = 0\).
Phương pháp giải:
Xét phương trình bậc hai một ẩn \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\), với \(b = 2b'\) và \(\Delta ' = b{'^2} - ac\)
+ Nếu \(\Delta ' > 0\) thì phương trình có hai nghiệm phân biệt: \({x_1} = \frac{{ - b' + \sqrt {\Delta '} }}{a};{x_2} = \frac{{ - b - \sqrt {\Delta '} }}{a}\).
+ Nếu \(\Delta ' = 0\) thì phương trình có nghiệm kép: \({x_1} = {x_2} = \frac{{ - b'}}{a}\).
+ Nếu \(\Delta ' < 0\) thì phương trình vô nghiệm.
Lời giải chi tiết:
a) Ta có: \(a = 3,b' = 4,c = - 3\) và \(\Delta ' = {4^2} - 3.\left( { - 3} \right) = 25 > 0\).
Do đó, phương trình có hai nghiệm phân biệt: \({x_1} = \frac{{ - 4 + \sqrt {25} }}{3} = \frac{1}{3};{x_2} = \frac{{ - 4 - \sqrt {25} }}{3} = - 3\).
b) Ta có: \(a = 1,b' = 3\sqrt 2 ,c = 2\) và \(\Delta ' = {\left( {3\sqrt 2 } \right)^2} - 1.2 = 16 > 0\).
Do đó, phương trình có hai nghiệm phân biệt: \({x_1} = - 3\sqrt 2 + 4;{x_2} = - 3\sqrt 2 - 4\)
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 4 trang 13 SGK Toán 9 Kết nối tri thức
Thực hiện các bước sau để giải phương trình: \(2{x^2} - 8x + 3 = 0\).
a) Chuyển hạng tử tự do sang vế phải.
b) Chia cả hai vế của phương trình cho hệ số của \({x^2}\).
c) Thêm vào hai vế của phương trình nhận được ở câu b với cùng một số để vế trái có thể biến đổi thành một bình phương. Từ đó tìm nghiệm x.
Phương pháp giải:
a) Chuyển hạng tử tự do của phương trình sang vế phải ta được phương trình \(2{x^2} - 8x = - 3\).
b) Chia cả hai vế của phương trình cho hệ số của \({x^2}\) ta được: \({x^2} - 4x = \frac{{ - 3}}{2}\).
c) Các bước giải phương trình:
+ Bước 1: Cộng thêm 4 vào 2 vế để đưa phương trình về dạng: \({A^2} = B\left( {B \ge 0} \right)\).
+ Bước 2: Nếu \({A^2} = B\left( {B \ge 0} \right)\) thì \(A = \sqrt B \) hoặc \(A = - \sqrt B \). Giải các phương trình đó và kết luận.
Lời giải chi tiết:
a) Chuyển hạng tử tự do của phương trình sang vế phải ta được phương trình \(2{x^2} - 8x = - 3\).
b) Chia cả hai vế của phương trình cho hệ số của \({x^2}\) ta được: \({x^2} - 4x = \frac{{ - 3}}{2}\).
c) \({x^2} - 4x = \frac{{ - 3}}{2}\)
\({x^2} - 4x + 4 = \frac{{ - 3}}{2} + 4\)
\({\left( {x - 2} \right)^2} = \frac{5}{2}\)
\(x - 2 = \frac{{\sqrt {10} }}{2}\) hoặc \(x - 2 = - \frac{{\sqrt {10} }}{2}\)
\(x = 2 + \frac{{\sqrt {10} }}{2}\) \(x = 2 - \frac{{\sqrt {10} }}{2}\)
Vậy phương trình có hai nghiệm \(x = 2 + \frac{{\sqrt {10} }}{2}\); \(x = 2 - \frac{{\sqrt {10} }}{2}\).
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 5 trang 14SGK Toán 9 Kết nối tri thức
Áp dụng công thức nghiệm, giải các phương trình sau:
a) \(2{x^2} - 5x + 1 = 0\);
b) \({x^2} + 8x + 16 = 0\);
c) \({x^2} - x + 1 = 0\).
Phương pháp giải:
Xét phương trình bậc hai một ẩn \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\). Tính biệt thức \(\Delta = {b^2} - 4ac\).
+ Nếu \(\Delta > 0\) thì phương trình có hai nghiệm phân biệt: \({x_1} = \frac{{ - b + \sqrt \Delta }}{{2a}};{x_2} = \frac{{ - b - \sqrt \Delta }}{{2a}}\).
+ Nếu \(\Delta = 0\) thì phương trình có nghiệm kép: \({x_1} = {x_2} = \frac{{ - b}}{{2a}}\).
+ Nếu \(\Delta < 0\) thì phương trình vô nghiệm.
Lời giải chi tiết:
a) Ta có: \(\Delta = {\left( { - 5} \right)^2} - 4.2.1 = 17 > 0\) nên phương trình có hai nghiệm phân biệt \({x_1} = \frac{{5 + \sqrt {17} }}{4};{x_2} = \frac{{5 - \sqrt {17} }}{4}\)
b) Ta có: \(\Delta = {8^2} - 4.1.16 = 0\) nên phương trình có nghiệm kép:\({x_1} = {x_2} = \frac{{ - 8}}{2} = - 4\)
c) Ta có: \(\Delta = {\left( { - 1} \right)^2} - 4.1.1 = - 3 < 0\) nên phương trình vô nghiệm.
Video hướng dẫn giải
Trả lời câu hỏi Thử thách nhỏ trang 14 SGK Toán 9 Kết nối tri thức
Pi hỏi: Có thể nói gì về nghiệm của phương trình bậc hai \(a{x^2} + bx + c = 0\) nếu a và c trái dấu?
Em hãy trả lời câu hỏi của anh Pi.
Phương pháp giải:
Xét phương trình bậc hai một ẩn \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có: \(\Delta = {b^2} - 4ac\)
Nếu a và c trái dấu thì tích \(ac < 0\). Từ đó, xét dấu của biệt thức \(\Delta \). Do đó, kết luận được số nghiệm của phương trình \(a{x^2} + bx + c = 0\).
Lời giải chi tiết:
Vì a và c trái dấu thì tích \(ac < 0\), suy ra: \( - ac > 0\).
Do đó, \(\Delta = {b^2} - 4ac > 0\). Suy ra, phương trình \(a{x^2} + bx + c = 0\) có hai nghiệm phân biệt.
Vậy nếu a và c trái dấu thì phương trình bậc hai \(a{x^2} + bx + c = 0\) có hai nghiệm phân biệt.
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 6 trang 15 SGK Toán 9 Kết nối tri thức
Xác định a, b’, c rồi dùng công thức nghiệm thu gọn giải các phương trình sau:
a) \(3{x^2} + 8x - 3 = 0\);
b) \({x^2} + 6\sqrt 2 x + 2 = 0\).
Phương pháp giải:
Xét phương trình bậc hai một ẩn \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\), với \(b = 2b'\) và \(\Delta ' = b{'^2} - ac\)
+ Nếu \(\Delta ' > 0\) thì phương trình có hai nghiệm phân biệt: \({x_1} = \frac{{ - b' + \sqrt {\Delta '} }}{a};{x_2} = \frac{{ - b - \sqrt {\Delta '} }}{a}\).
+ Nếu \(\Delta ' = 0\) thì phương trình có nghiệm kép: \({x_1} = {x_2} = \frac{{ - b'}}{a}\).
+ Nếu \(\Delta ' < 0\) thì phương trình vô nghiệm.
Lời giải chi tiết:
a) Ta có: \(a = 3,b' = 4,c = - 3\) và \(\Delta ' = {4^2} - 3.\left( { - 3} \right) = 25 > 0\).
Do đó, phương trình có hai nghiệm phân biệt: \({x_1} = \frac{{ - 4 + \sqrt {25} }}{3} = \frac{1}{3};{x_2} = \frac{{ - 4 - \sqrt {25} }}{3} = - 3\).
b) Ta có: \(a = 1,b' = 3\sqrt 2 ,c = 2\) và \(\Delta ' = {\left( {3\sqrt 2 } \right)^2} - 1.2 = 16 > 0\).
Do đó, phương trình có hai nghiệm phân biệt: \({x_1} = - 3\sqrt 2 + 4;{x_2} = - 3\sqrt 2 - 4\)
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng trang 15 SGK Toán 9 Kết nối tri thức
Giải bài toán trong tình huống mở đầu.
Tình huống mở đầu: Trên một mảnh đất hình chữ nhật có kích thước 28m x 16m, người ta dự định làm một bể bơi có đường đi xung quanh (H.6.9). Hỏi bề rộng của đường đi là bao nhiêu để diện tích của bể bơi là \(288{m^2}\)?
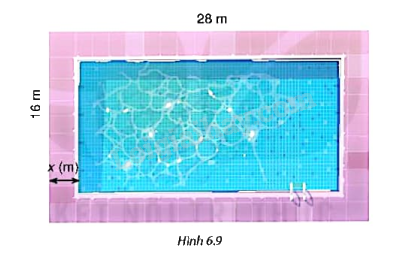
Phương pháp giải:
- Giải phương trình đã lập được ở HĐ3 để tìm x:
Xét phương trình bậc hai một ẩn \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\), với \(b = 2b'\) và \(\Delta ' = b{'^2} - ac\)
+ Nếu \(\Delta ' > 0\) thì phương trình có hai nghiệm phân biệt: \({x_1} = \frac{{ - b' + \sqrt {\Delta '} }}{a};{x_2} = \frac{{ - b - \sqrt {\Delta '} }}{a}\).
+ Nếu \(\Delta ' = 0\) thì phương trình có nghiệm kép: \({x_1} = {x_2} = \frac{{ - b'}}{a}\).
+ Nếu \(\Delta ' < 0\) thì phương trình vô nghiệm.
- Đối chiếu x vừa tìm được với điều kiện và đưa ra kết luận.
Lời giải chi tiết:
Theo kết quả của HĐ3 ta có: \(4{x^2} - 88x + 160 = 0\)
\({x^2} - 22x + 40 = 0\)
Ta có: \(\Delta ' = {11^2} - 1.40 = 81 > 0\).
Do đó, phương trình có hai nghiệm phân biệt:
\({x_1} = \frac{11 + \sqrt{81}}{1} = 20\left( {KTM} \right);{x_2} = \frac{11 - \sqrt{81}}{1}= 2\left( {TM} \right)\)
Vậy bề rộng của đường đi là 2m thì diện tích của bể bơi là \(288{m^2}\).
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng trang 15 SGK Toán 9 Kết nối tri thức
Giải bài toán trong tình huống mở đầu.
Tình huống mở đầu: Trên một mảnh đất hình chữ nhật có kích thước 28m x 16m, người ta dự định làm một bể bơi có đường đi xung quanh (H.6.9). Hỏi bề rộng của đường đi là bao nhiêu để diện tích của bể bơi là \(288{m^2}\)?
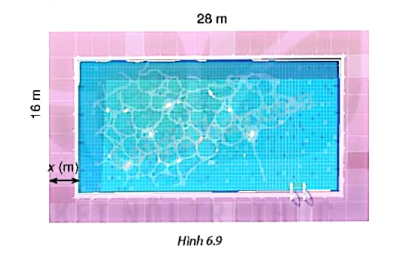
Phương pháp giải:
- Giải phương trình đã lập được ở HĐ3 để tìm x:
Xét phương trình bậc hai một ẩn \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\), với \(b = 2b'\) và \(\Delta ' = b{'^2} - ac\)
+ Nếu \(\Delta ' > 0\) thì phương trình có hai nghiệm phân biệt: \({x_1} = \frac{{ - b' + \sqrt {\Delta '} }}{a};{x_2} = \frac{{ - b - \sqrt {\Delta '} }}{a}\).
+ Nếu \(\Delta ' = 0\) thì phương trình có nghiệm kép: \({x_1} = {x_2} = \frac{{ - b'}}{a}\).
+ Nếu \(\Delta ' < 0\) thì phương trình vô nghiệm.
- Đối chiếu x vừa tìm được với điều kiện và đưa ra kết luận.
Lời giải chi tiết:
Theo kết quả của HĐ3 ta có: \(4{x^2} - 88x + 160 = 0\)
\({x^2} - 22x + 40 = 0\)
Ta có: \(\Delta ' = {11^2} - 1.40 = 81 > 0\).
Do đó, phương trình có hai nghiệm phân biệt:
\({x_1} = \frac{11 + \sqrt{81}}{1} = 20\left( {KTM} \right);{x_2} = \frac{11 - \sqrt{81}}{1}= 2\left( {TM} \right)\)
Vậy bề rộng của đường đi là 2m thì diện tích của bể bơi là \(288{m^2}\).
Mục 3 trong SGK Toán 9 tập 2 - Kết nối tri thức tập trung vào việc ôn tập chương 3: Hệ hai phương trình tuyến tính. Nội dung chính bao gồm việc củng cố các phương pháp giải hệ phương trình, ứng dụng giải quyết các bài toán thực tế và nâng cao kỹ năng tư duy toán học. Việc nắm vững kiến thức này là nền tảng quan trọng cho các chương học tiếp theo và kỳ thi cuối học kỳ.
Bài tập này yêu cầu học sinh vận dụng phương pháp thế để giải các hệ phương trình tuyến tính. Phương pháp thế bao gồm các bước: biểu diễn một ẩn theo ẩn còn lại từ một phương trình, thay biểu thức đó vào phương trình còn lại để tìm ẩn còn lại, sau đó thay giá trị vừa tìm được vào biểu thức ban đầu để tìm ẩn còn lại.
Lời giải chi tiết cho từng hệ phương trình sẽ được trình bày cụ thể, kèm theo các bước giải thích rõ ràng để học sinh dễ dàng theo dõi và hiểu bài.
Bài tập này yêu cầu học sinh sử dụng phương pháp cộng đại số để giải các hệ phương trình tuyến tính. Phương pháp cộng đại số bao gồm các bước: nhân các phương trình với các hệ số thích hợp để các hệ số của một ẩn bằng nhau hoặc đối nhau, cộng các phương trình lại với nhau để loại bỏ ẩn đó, sau đó giải phương trình còn lại để tìm ẩn còn lại, và thay giá trị vừa tìm được vào một trong các phương trình ban đầu để tìm ẩn còn lại.
Tương tự như bài 1, lời giải chi tiết sẽ được cung cấp cho từng hệ phương trình.
Bài tập này yêu cầu học sinh vận dụng kiến thức về hệ phương trình để giải các bài toán thực tế. Các bước giải bài toán bằng cách lập hệ phương trình bao gồm: xác định ẩn, lập hệ phương trình dựa trên các điều kiện của bài toán, giải hệ phương trình, và kiểm tra lại kết quả.
Ví dụ:
Một người đi xe máy từ A đến B với vận tốc 40km/h. Sau khi đi được 30 phút, người đó tăng vận tốc lên 50km/h và đến B muộn hơn 10 phút so với dự kiến. Tính quãng đường AB.
Lời giải:
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các em học sinh sẽ tự tin hơn trong việc giải các bài tập mục 3 trang 13, 14, 15 SGK Toán 9 tập 2 - Kết nối tri thức. Chúc các em học tập tốt và đạt kết quả cao!