Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9. Bài viết này sẽ hướng dẫn bạn cách giải bài tập 8.6 trang 63 SGK Toán 9 tập 2 - Kết nối tri thức một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và tự tin hơn trong các kỳ thi.
Gieo đồng thời hai con xúc xắc cân đối, đồng chất I và II. Tính xác suất của các biến cố sau: E: “Có đúng một con xúc xắc xuất hiện mặt 6 chấm”; F: “Có ít nhất một con xúc xắc xuất hiện mặt 6 chấm”; G: “Tích của hai chấm xuất hiện trên hai con xúc xắc nhỏ hơn hoặc bằng 6”.
Đề bài
Gieo đồng thời hai con xúc xắc cân đối, đồng chất I và II. Tính xác suất của các biến cố sau:
E: “Có đúng một con xúc xắc xuất hiện mặt 6 chấm”;
F: “Có ít nhất một con xúc xắc xuất hiện mặt 6 chấm”;
G: “Tích của hai chấm xuất hiện trên hai con xúc xắc nhỏ hơn hoặc bằng 6”.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Cách tính xác suất của một biến cố E:
Bước 1. Mô tả không gian mẫu của phép thử. Từ đó xác định số phần tử của không gian mẫu \(\Omega \).
Bước 2. Chứng tỏ các kết quả có thể của phép thử là đồng khả năng.
Bước 3. Mô tả kết quả thuận lợi của biến cố E. Từ đó xác định số kết quả thuận lợi cho biến cố E.
Bước 4. Lập tỉ số giữa số kết quả thuận lợi cho biến cố E với số phần tử của không gian mẫu \(\Omega \).
Lời giải chi tiết
Kết quả phép thử được viết dưới dạng (a, b) trong đó a, b lần lượt là số chấm xuất hiện trên hai con xúc xắc I và II.
Ta có bảng miêu tả không gian mẫu là:
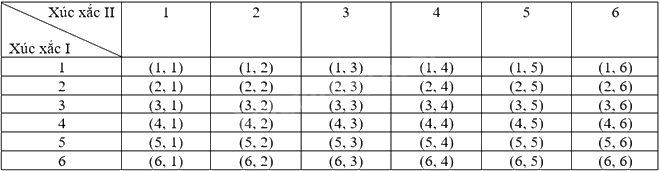
Do đó, số phần tử của không gian mẫu \(\Omega \) là 36.
Vì gieo đồng thời hai con xúc xắc cân đối, đồng chất nên các kết quả có thể xảy là đồng khả năng.
Có 10 kết quả thuận lợi của biến cố E là: (1, 6), (2, 6), (3, 6), (4, 6), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5). Do đó, \(P\left( E \right) = \frac{{10}}{{36}} = \frac{5}{{18}}\).
Có 11 kết quả thuận lợi của biến cố F là: (1, 6), (2, 6), (3, 6), (4, 6), (5, 6), (6, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5). Do đó, \(P\left( F \right) = \frac{{11}}{{36}}\).
Có 14 kết quả thuận lợi của biến cố G là: (1, 1), (2, 1), (3, 1), (4, 1), (5, 1), (6, 1), (1, 2), (2, 2), (3, 2), (1, 3), (2, 3), (1, 4), (1, 5), (1, 6). Do đó, \(P\left( G \right) = \frac{{14}}{{36}} = \frac{7}{{18}}\).
Bài tập 8.6 trang 63 SGK Toán 9 tập 2 - Kết nối tri thức thuộc chương trình học về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế liên quan đến việc xác định hàm số và tính giá trị của hàm số tại một điểm cho trước.
Bài tập 8.6 thường có dạng như sau:
Để giải quyết bài tập 8.6 một cách hiệu quả, bạn cần nắm vững các kiến thức sau:
Bài toán: Một người nông dân trồng cây cam. Chi phí trồng và chăm sóc cây cam là 5 triệu đồng. Mỗi quả cam bán được với giá 10.000 đồng. Hãy viết hàm số biểu diễn lợi nhuận thu được khi bán x quả cam.
Giải:
Gọi L là lợi nhuận thu được khi bán x quả cam. Ta có:
L = 10.000x - 5.000.000
Vậy hàm số biểu diễn lợi nhuận thu được khi bán x quả cam là L = 10.000x - 5.000.000.
Để củng cố kiến thức và kỹ năng giải bài tập 8.6, bạn có thể luyện tập thêm với các bài tập tương tự trong SGK Toán 9 tập 2 - Kết nối tri thức và các tài liệu tham khảo khác.
Kiến thức về hàm số bậc nhất là nền tảng quan trọng cho việc học các kiến thức toán học nâng cao hơn, đặc biệt là trong chương trình học lớp 10, 11 và 12. Việc nắm vững kiến thức này sẽ giúp bạn tự tin hơn trong các kỳ thi và có thể áp dụng vào các bài toán thực tế.
Hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức và kỹ năng cần thiết để giải bài tập 8.6 trang 63 SGK Toán 9 tập 2 - Kết nối tri thức một cách hiệu quả. Chúc bạn học tập tốt!