Bài tập 6.5 trang 8 SGK Toán 9 tập 2 thuộc chương trình Toán 9 Kết nối tri thức, yêu cầu học sinh vận dụng kiến thức về hệ phương trình bậc nhất hai ẩn để giải các bài toán thực tế. Bài tập này thường gặp trong các kỳ thi và kiểm tra, do đó việc nắm vững phương pháp giải là rất quan trọng.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 6.5 trang 8 SGK Toán 9 tập 2, giúp các em học sinh hiểu rõ bản chất của bài toán và tự tin giải các bài tập tương tự.
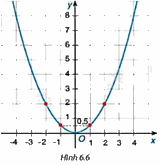
Biết đường cong trong Hình 6.6 là một parabol (y = a{x^2}). a) Tìm hệ số a. b) Tìm tung độ của điểm thuộc parabol có hoành độ (x = - 2). c) Tìm các điểm thuộc parabol có tung độ (y = 8).
Đề bài
Biết đường cong trong Hình 6.6 là một parabol \(y = a{x^2}\).
a) Tìm hệ số a.
b) Tìm tung độ của điểm thuộc parabol có hoành độ \(x = - 2\).
c) Tìm các điểm thuộc parabol có tung độ \(y = 8\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Điểm (1; 0,5) thuộc parabol \(y = a{x^2}\) nên thay tọa độ điểm (1; 0,5) vào hàm số \(y = a{x^2}\) ta tìm được a.
b) Thay \(x = - 2\) vào hàm số \(y = 0,5{x^2}\) để tìm tung độ y.
c) Thay \(y = 8\) vào hàm số \(y = 0,5{x^2}\) để tìm hoành độ x.
Lời giải chi tiết
a) Từ đồ thị hàm số ta có, điểm (1; 0,5) thuộc parabol \(y = a{x^2}\) nên: \(0,5 = a{.1^2} \Rightarrow a = 0,5\)
b) Với \(a = 0,5\) ta có: \(y = 0,5{x^2}\)
Thay \(x = - 2\) vào hàm số \(y = 0,5{x^2}\) ta có: \(y = 0,5.{\left( { - 2} \right)^2} = 0,5.4 = 2\).
c) Thay \(y = 8\) vào hàm số \(y = 0,5{x^2}\) ta có: \(8 = 0,5{x^2} \Rightarrow {x^2} = 16 \Rightarrow x = \pm 4\).
Các điểm thuộc parabol có tung độ \(y = 8\) là: \(\left( { - 4;8} \right);\left( {4;8} \right)\).
Bài tập 6.5 trang 8 SGK Toán 9 tập 2 yêu cầu giải bài toán về việc tìm số tiền mà mỗi bạn An và Bình có, dựa trên thông tin về tổng số tiền và mối quan hệ giữa số tiền của hai bạn. Để giải bài toán này, chúng ta sẽ sử dụng phương pháp giải hệ phương trình bậc nhất hai ẩn.
An và Bình có tổng cộng 120 nghìn đồng. Nếu An cho Bình 20 nghìn đồng thì số tiền của Bình gấp đôi số tiền của An. Hỏi lúc đầu mỗi bạn có bao nhiêu tiền?
1. Đặt ẩn:
2. Lập phương trình:
Dựa vào đề bài, ta có hệ phương trình sau:
3. Giải hệ phương trình:
Từ phương trình (1), ta có: y = 120 - x
Thay y = 120 - x vào phương trình (2), ta được:
120 - x + 20 = 2(x - 20)
140 - x = 2x - 40
3x = 180
x = 60
Thay x = 60 vào phương trình y = 120 - x, ta được:
y = 120 - 60 = 60
Vậy lúc đầu An có 60 nghìn đồng và Bình có 60 nghìn đồng.
Các bài tập về hệ phương trình bậc nhất hai ẩn thường xuất hiện trong các dạng sau:
Để nắm vững kiến thức về hệ phương trình bậc nhất hai ẩn, các em học sinh nên luyện tập thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Giaitoan.edu.vn sẽ tiếp tục cung cấp các lời giải chi tiết và hướng dẫn giải các bài tập Toán 9 khác, giúp các em học Toán 9 hiệu quả hơn.
| Công thức | Mô tả |
|---|---|
| x + y = S | Tổng của hai số |
| x - y = D | Hiệu của hai số |
| S = v * t | Quãng đường, vận tốc, thời gian |