Bài tập 5.29 trang 110 SGK Toán 9 tập 1 thuộc chương Hàm số bậc nhất. Đây là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng vận dụng kiến thức về hàm số bậc nhất vào giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 5.29, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Khi chuyển động, giả sử đầu mũi kim dài của một chiếc đồng hồ vạch nên một đường tròn, kí hiệu là (T1), trong khi đầu mũi kim ngắn vạch nên một đường tròn khác, kí hiệu là (T2). a) Hai đường tròn (T1) và (T2) có vị trí tương đối như thế nào? b) Giả sử bán kính của (T1) và (T2) lần lượt là R1 và R2. Người ta vẽ trên mặt đồng hồ một họa tiết hình tròn có tâm nằm cách điểm trục kim đồng hồ một khoảng bằng (frac{1}{2}{{rm{R}}_1}) và có bán kính bằng (frac{1}{2}{{rm{R}}_2}). Hãy cho biết vị
Đề bài
Khi chuyển động, giả sử đầu mũi kim dài của một chiếc đồng hồ vạch nên một đường tròn, kí hiệu là (T1), trong khi đầu mũi kim ngắn vạch nên một đường tròn khác, kí hiệu là (T2).
a) Hai đường tròn (T1) và (T2) có vị trí tương đối như thế nào?
b) Giả sử bán kính của (T1) và (T2) lần lượt là R1 và R2. Người ta vẽ trên mặt đồng hồ một họa tiết hình tròn có tâm nằm cách điểm trục kim đồng hồ một khoảng bằng \(\frac{1}{2}{{\rm{R}}_1}\) và có bán kính bằng \(\frac{1}{2}{{\rm{R}}_2}\). Hãy cho biết vị trí tương đối của đường tròn (T3) đối với mỗi đường tròn (T1) và (T2). Vẽ ba đường tròn đó nếu R1 = 3 cm, R2 = 2 cm.

Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Hai đường tròn (T1) và (T2) là hai đường tròn đồng tâm, (T1) chứa (T2).
b) So sánh khoảng cách giữa tâm của 2 đường tròn với tổng hiệu hai bán kính, từ đó suy ra vị trí tương đối của hai đường tròn.
Lời giải chi tiết
a) Hai đường tròn (T1) và (T2) là hai đường tròn đồng tâm, (T1) chứa (T2).
b) Gọi tâm của (T1) là O, tâm của (T3) là O’
Xét \(\left( {{T_1}} \right)\) và \(\left( {{T_3}} \right)\), ta có:
\({{\rm{R}}_3} = \frac{1}{2}{{\rm{R}}_2}\); \({{\rm{R}}_1} + {{\rm{R}}_3} > {{\rm{R}}_1}{\rm{ > }}\frac{1}{2}{{\rm{R}}_1} = {\rm{OO'}}\) hay \({{\rm{R}}_1} + {R_3} > {\rm{OO'}}\)
\(\begin{array}{l}{R_1} - {R_3} = {R_1} - \frac{1}{2}{R_2}\\ = \frac{1}{2}{R_1} + \frac{1}{2}{R_1} - \frac{1}{2}{R_2}\\ = \frac{1}{2}{R_1} + \left( {\frac{1}{2}{R_1} - \frac{1}{2}{R_2}} \right)\\ = \frac{1}{2}{R_1} + \frac{1}{2}\left( {{R_1} - {R_2}} \right)\end{array}\)
Vì \({R_1} - {R_2} > 0\) nên \(\frac{1}{2}{R_1} + \frac{1}{2}\left( {{R_1} - {R_2}} \right) > \frac{1}{2}{R_1} = OO'\) hay \({{\rm{R}}_1} - {{\rm{R}}_3}{\rm{ > OO'}}\)hay \({\rm{OO'}} < {{\rm{R}}_1} - {{\rm{R}}_3}\)
Vậy (T1) đựng (T3).
Xét \(\left( {{T_2}} \right)\) và \(\left( {{T_3}} \right)\), ta có:
\({{\rm{R}}_3} = \frac{1}{2}{{\rm{R}}_2}\); \({{\rm{R}}_2}{\rm{ - }}{{\rm{R}}_3} = {R_2} - \frac{1}{2}{R_2} = \frac{1}{2}{R_2} < \frac{1}{2}{R_1} = OO'\) hay \({R_2} - {R_3} < OO'\)
\({R_2} + {R_3} = {R_2} + \frac{1}{2}{R_2} = \frac{3}{2}{R_2}\).
TH1: \(\frac{3}{2}{R_2} > \frac{1}{2}{R_1}\) hay \(3{R_2} > {R_1}\) thì \({R_2} + {R_3} > OO'\)
Suy ra \({R_2} - {R_3} < OO' < {R_2} + {R_3}\)
Vậy (T2) và (T3) cắt nhau.
TH2: \(\frac{3}{2}{R_2} = \frac{1}{2}{R_1}\) hay \(3{R_2} = {R_1}\) thì \({R_2} + {R_3} = OO'\)
Vậy (T2) tiếp xúc ngoài với (T3).
TH2: \(\frac{3}{2}{R_2} < \frac{1}{2}{R_1}\) hay \(3{R_2} < {R_1}\) thì \({R_2} + {R_3} < OO'\)
Vậy (T2) và (T3) ở ngoài nhau.
+ Với R1 = 3 cm, R2 = 2 cm, so sánh \(3{R_2}\) với \({R_1}\), ta được \(3{R_2} = 3.2 = 6 > 3 = {R_1}\), khi đó (T2) và (T3) cắt nhau.
\(\begin{array}{l}\left( {{T_3}} \right):{R_3} = \frac{1}{2}.2 = 1cm\\OO' = \frac{1}{2}{R_1} = \frac{1}{2}.3 = \frac{3}{2}cm\end{array}\)
Ta có hình vẽ sau:
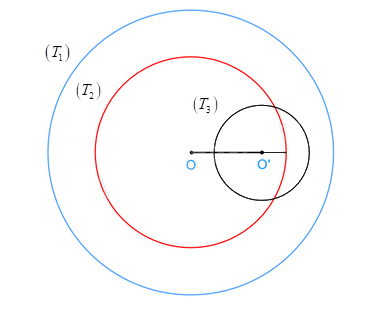
Bài tập 5.29 trang 110 SGK Toán 9 tập 1 - Kết nối tri thức yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết một bài toán thực tế liên quan đến việc xác định hàm số và tính giá trị của hàm số tại một điểm cho trước. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các khái niệm và phương pháp sau:
Đề bài: (Bài tập 5.29 trang 110 SGK Toán 9 tập 1 - Kết nối tri thức) Một người đi xe máy từ A đến B với vận tốc 40 km/h. Hỏi người đó đi hết bao lâu nếu quãng đường AB dài 120 km?
Lời giải:
Thời gian được tính bằng công thức: t = s / v
t = 120 km / 40 km/h = 3 giờ
Bài tập 5.29 là một bài toán ứng dụng thực tế, giúp học sinh hiểu rõ hơn về mối liên hệ giữa vận tốc, quãng đường và thời gian. Bài tập này cũng rèn luyện kỹ năng giải toán bằng cách áp dụng công thức và phân tích đề bài một cách logic.
Để mở rộng bài tập, chúng ta có thể thay đổi các yếu tố của bài toán, ví dụ như thay đổi vận tốc hoặc quãng đường, và yêu cầu học sinh tính lại thời gian. Hoặc chúng ta có thể đặt ra các câu hỏi liên quan đến việc tính chi phí nhiên liệu hoặc các yếu tố khác liên quan đến việc đi lại.
Để củng cố kiến thức về hàm số bậc nhất và các ứng dụng của nó, các em học sinh có thể tham khảo các bài tập tương tự sau:
Bài tập 5.29 trang 110 SGK Toán 9 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng vận dụng kiến thức về hàm số bậc nhất vào giải quyết các bài toán thực tế. Hy vọng rằng lời giải chi tiết và phân tích của Giaitoan.edu.vn sẽ giúp các em học sinh hiểu rõ hơn về bài tập này và tự tin làm bài tập.