Bài học này sẽ cung cấp cho bạn kiến thức nền tảng về vị trí tương đối của hai đường tròn trong chương trình Toán 9 Kết nối tri thức. Chúng ta sẽ cùng nhau khám phá các trường hợp có thể xảy ra và cách xác định chúng.
Nắm vững lý thuyết này là bước quan trọng để giải quyết các bài toán liên quan đến đường tròn, một chủ đề trọng tâm trong chương trình học.
1. Hai đường tròn cắt nhau
1. Hai đường tròn cắt nhau
Nếu hai đường tròn có đúng một điểm chung thì ta gọi đó là hai đường tròn cắt nhau. Hai điểm chung đó là hai giao điểm của chúng. |
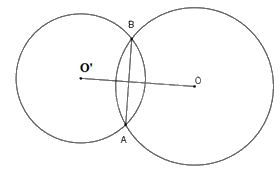
Hai đường tròn (O;R) và (O;R’) cắt nhau khi
\(R - R' < OO' < R + R'\) (với \(R > R'\))
Ví dụ: Cho OO’ = 5cm, khi đó hai đường tròn (O;4cm) và (O’;3cm) cắt nhau vì:
4cm – 3cm = 1cm < 5cm < 7cm = 4cm + 3cm.
2. Hai đường tròn tiếp xúc với nhau
Nếu hai đường tròn có duy nhất một điểm chung thì ta nói đó là hai đường tròn tiếp xúc với nhau. Điểm chung đó gọi là tiếp điểm của chúng. |
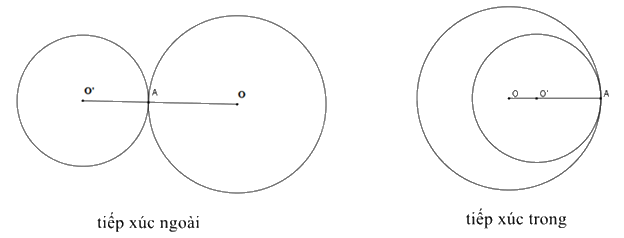
+ Hai đường tròn (O;R) và (O’;R’) tiếp xúc ngoài khi \(OO' = R + R'\).
+ Hai đường tròn (O;R) và (O’;R’) tiếp xúc trong khi \(OO' = R - R'\left( {R > R'} \right)\).
Nếu hai đường tròn tiếp xúc với nhau thì tiếp điểm thẳng hàng với hai tâm.
Ví dụ:
Cho OO’ = 5cm, khi đó hai đường tròn (O;3cm) và (O’;2cm) tiếp xúc ngoài với nhau vì 5cm = 3cm + 2cm.
Cho OO’ = 3cm, khi đó hai đường tròn (O;8cm) và (O’;5cm) tiếp xúc trong với nhau vì 3cm = 8cm - 5cm.
3. Hai đường tròn không giao nhau
Nếu hai đường tròn không có điểm chung nào thi ta nói đó là hai đường tròn không giao nhau. |
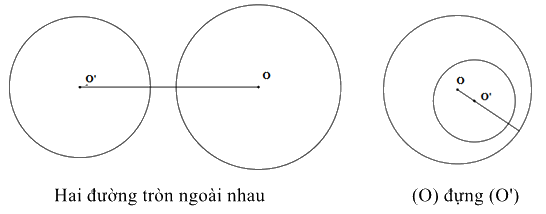
- Hai đường tròn (O;R) và (O’;R’) ngoài nhau khi \(OO' > R + R'\);
- Đường tròn (O;R) đựng đường tròn (O’;R’) khi \(R > R'\) và \(OO' < R - R'\).
Khi O trùng với O’ và \(R \ne R'\) thì ta có hai đường tròn đồng tâm.
Ví dụ: Cho đường tròn (O;3cm) và (O’;4cm) có \(OO' > 8cm\) thì \(OO' = 8cm > 3cm + 4cm = R + R'\) nên (O;3cm) và (O’;4cm) là hai đường tròn ngoài nhau.
Bảng tổng kết vị trí tương đối của hai đường tròn
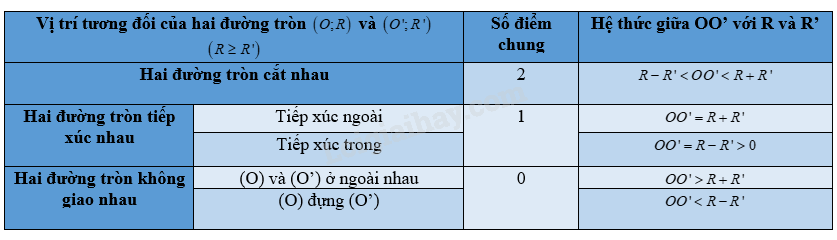
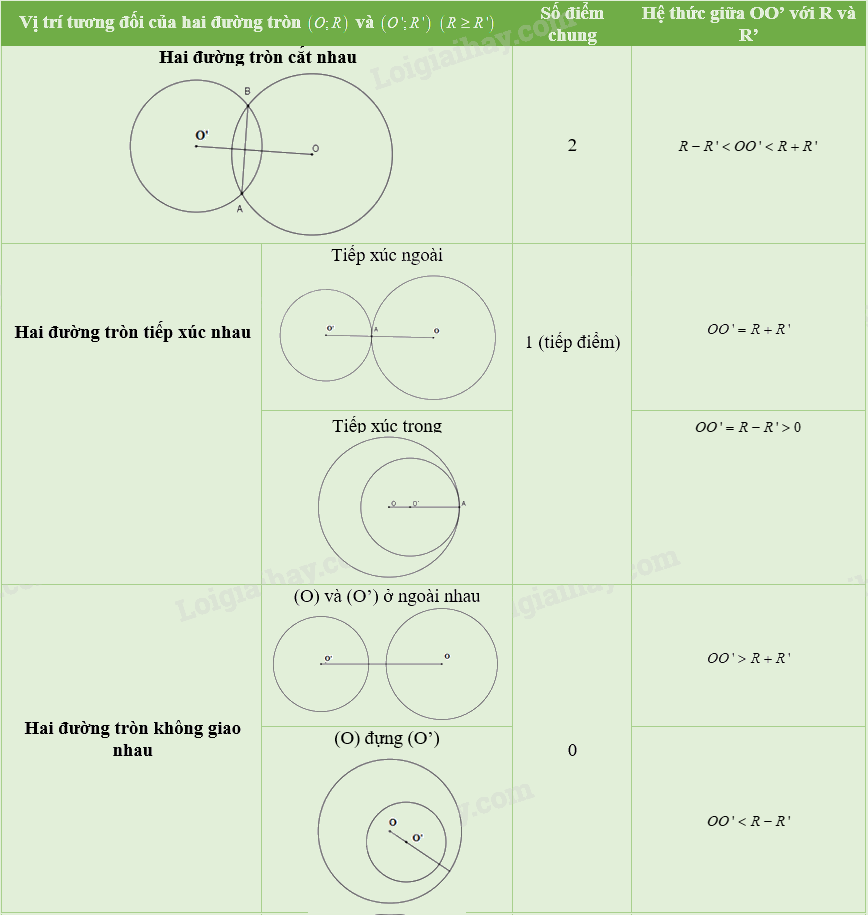
Trong hình học, việc xác định vị trí tương đối giữa các đối tượng là một kỹ năng quan trọng. Đối với hai đường tròn, có bốn trường hợp vị trí tương đối có thể xảy ra. Chúng ta sẽ cùng nhau tìm hiểu chi tiết từng trường hợp này.
Hai đường tròn không giao nhau khi khoảng cách giữa hai tâm lớn hơn tổng hai bán kính. Điều này có nghĩa là hai đường tròn nằm hoàn toàn ngoài nhau, không có điểm chung nào.
Công thức: d > r1 + r2 (với d là khoảng cách giữa hai tâm, r1 và r2 là bán kính của hai đường tròn)
Hai đường tròn tiếp xúc ngoài khi khoảng cách giữa hai tâm bằng tổng hai bán kính. Trong trường hợp này, hai đường tròn chỉ có một điểm chung duy nhất, gọi là điểm tiếp xúc.
Công thức: d = r1 + r2
Hai đường tròn cắt nhau khi khoảng cách giữa hai tâm nhỏ hơn tổng hai bán kính nhưng lớn hơn hiệu hai bán kính. Điều này có nghĩa là hai đường tròn có hai điểm chung.
Công thức: |r1 - r2| < d < r1 + r2
Hai đường tròn tiếp xúc trong khi khoảng cách giữa hai tâm bằng hiệu hai bán kính. Trong trường hợp này, một đường tròn nằm hoàn toàn bên trong đường tròn còn lại và chúng có một điểm chung duy nhất.
Công thức: d = |r1 - r2|
Một đường tròn nằm trong đường tròn kia khi khoảng cách giữa hai tâm nhỏ hơn hiệu hai bán kính. Trong trường hợp này, một đường tròn nằm hoàn toàn bên trong đường tròn còn lại và không có điểm chung nào.
Công thức: d < |r1 - r2|
Cho hai đường tròn (O1; 3cm) và (O2; 2cm) có khoảng cách giữa hai tâm O1O2 = 5cm. Hãy xác định vị trí tương đối của hai đường tròn này.
Giải:
Vì d = r1 + r2 nên hai đường tròn tiếp xúc ngoài.
1. Cho hai đường tròn (O; 4cm) và (O'; 1cm) có khoảng cách giữa hai tâm OO' = 3cm. Xác định vị trí tương đối của hai đường tròn này.
2. Cho hai đường tròn (A; 5cm) và (B; 3cm) có khoảng cách giữa hai tâm AB = 7cm. Xác định vị trí tương đối của hai đường tròn này.
Việc nắm vững lý thuyết về vị trí tương đối của hai đường tròn là nền tảng quan trọng để giải quyết các bài toán hình học. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải toán của bạn.