Giaitoan.edu.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 1 trang 60, 61 sách giáo khoa Toán 9 tập 2 chương trình Kết nối tri thức. Bài viết này sẽ giúp học sinh nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt trong học tập.
Chúng tôi cung cấp không chỉ đáp án mà còn cả phương pháp giải, giúp các em hiểu rõ bản chất của bài toán và áp dụng vào các bài tập tương tự.
Bạn Tùng gieo một con xúc xắc liên tiếp hai lần. Xét các biến cố sau: E: “Cả hai lần gieo con xúc xắc đều xuất hiện mặt có số chấm là số nguyên tố”. F: “Cả hai lần gieo con xúc xắc đều không xuất hiện mặt có số chấm là số chẵn”. a) Phép thử là gì? b) Giả sử số chấm xuất hiện trên con xúc xắc trong lần gieo thứ nhất, thứ hai tương ứng là 2 chấm và 5 chấm. Khi đó, biến cố nào xảy ra? Biến cố nào không xảy ra?
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động trang 60 SGK Toán 9 Kết nối tri thức
Bạn Tùng gieo một con xúc xắc liên tiếp hai lần. Xét các biến cố sau:
E: “Cả hai lần gieo con xúc xắc đều xuất hiện mặt có số chấm là số nguyên tố”.
F: “Cả hai lần gieo con xúc xắc đều không xuất hiện mặt có số chấm là số chẵn”.
a) Phép thử là gì?
b) Giả sử số chấm xuất hiện trên con xúc xắc trong lần gieo thứ nhất, thứ hai tương ứng là 2 chấm và 5 chấm. Khi đó, biến cố nào xảy ra? Biến cố nào không xảy ra?
Phương pháp giải:
Sử dụng kiến thức về phép thử để tìm phép thử: Một hoặc một số hành động, thực nghiệm được tiến hành liên tiếp hay đồng thời mà kết quả của chúng không thể biết được trước khi thực hiện nhưng có thể liệt kê các kết quả có thể xảy ra, được gọi là một phép thử ngẫu nhiên, gọi tắt là phép thử.
Lời giải chi tiết:
a) Phép thử là: Gieo một con xúc xắc liên tiếp hai lần.
b) Vì 2 và 5 đều là có số nguyên tố nên biến cố E xảy ra.
Vì 2 là số chẵn và 5 là số lẻ nên biến cố F không xảy ra.
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 1 trang 61SGK Toán 9 Kết nối tri thức
Bạn Hoàng lấy ngẫu nhiên một quả cầu từ một túi đựng 2 quả cầu gồm một quả màu đen và một quả màu trắng, có cùng khối lượng và kích thước. Bạn Hải rút ngẫu nhiên một tấm thẻ từ một hộp đựng 3 tấm thẻ A, B, C.
a) Mô tả không gian mẫu của phép thử.
b) Xét các biến cố sau:
E: “Bạn Hoàng lấy được quả cầu màu đen”.
F: “Bạn Hoàng lấy được quả cầu màu trắng và bạn Hải không rút được tấm thẻ A”.
Hãy mô tả các kết quả thuận lợi cho hai biến cố E và F.
Phương pháp giải:
a) Sử dụng kiến thức về phép thử để tìm phép thử: Một hoặc một số hành động, thực nghiệm được tiến hành liên tiếp hay đồng thời mà kết quả của chúng không thể biết được trước khi thực hiện nhưng có thể liệt kê các kết quả có thể xảy ra, được gọi là một phép thử ngẫu nhiên, gọi tắt là phép thử.
Có thể tìm không gian mẫu của phép tử bằng cách lập bảng.
b) Cách tìm kết quả thuận lợi của biến cố E.
+ Mô tả không gian mẫu của phép thử.
+ Tìm kết quả của phép thử làm cho biến cố xảy ra, đó là kết quả thuận lợi cho biến cố E.
Lời giải chi tiết:
a) Phép thử là Hoàng lấy ngẫu nhiên một quả cầu từ một túi đựng 2 quả cầu gồm một quả màu đen và một quả màu trắng, Hải rút ngẫu nhiên một tấm thẻ từ một hộp đựng 3 tấm thẻ A, B, C.
Kết quả của phép thử là (a, b) trong đó a và b tương ứng là màu của quả bóng và chữ ghi trên tấm thẻ.
Ta liệt kê được tất cả các kết quả có thể của phép thử bằng cách lập bảng:
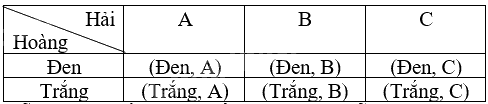
Mỗi ô là một kết quả có thể. Không gian mẫu là tập hợp 6 ô của bảng trên.
Do đó, không gian mẫu của phép thử là \(\Omega = \){(Đen, A), (Đen, B), (Đen, C), (Trắng, A), (Trắng, B), (Trắng, C)}.
b) Các kết quả thuận lợi của biến cố E là: (Đen, A), (Đen, B), (Đen, C).
Các kết quả thuận lợi của biến cố F là: (Trắng, B), (Trắng, C).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động trang 60 SGK Toán 9 Kết nối tri thức
Bạn Tùng gieo một con xúc xắc liên tiếp hai lần. Xét các biến cố sau:
E: “Cả hai lần gieo con xúc xắc đều xuất hiện mặt có số chấm là số nguyên tố”.
F: “Cả hai lần gieo con xúc xắc đều không xuất hiện mặt có số chấm là số chẵn”.
a) Phép thử là gì?
b) Giả sử số chấm xuất hiện trên con xúc xắc trong lần gieo thứ nhất, thứ hai tương ứng là 2 chấm và 5 chấm. Khi đó, biến cố nào xảy ra? Biến cố nào không xảy ra?
Phương pháp giải:
Sử dụng kiến thức về phép thử để tìm phép thử: Một hoặc một số hành động, thực nghiệm được tiến hành liên tiếp hay đồng thời mà kết quả của chúng không thể biết được trước khi thực hiện nhưng có thể liệt kê các kết quả có thể xảy ra, được gọi là một phép thử ngẫu nhiên, gọi tắt là phép thử.
Lời giải chi tiết:
a) Phép thử là: Gieo một con xúc xắc liên tiếp hai lần.
b) Vì 2 và 5 đều là có số nguyên tố nên biến cố E xảy ra.
Vì 2 là số chẵn và 5 là số lẻ nên biến cố F không xảy ra.
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 1 trang 61SGK Toán 9 Kết nối tri thức
Bạn Hoàng lấy ngẫu nhiên một quả cầu từ một túi đựng 2 quả cầu gồm một quả màu đen và một quả màu trắng, có cùng khối lượng và kích thước. Bạn Hải rút ngẫu nhiên một tấm thẻ từ một hộp đựng 3 tấm thẻ A, B, C.
a) Mô tả không gian mẫu của phép thử.
b) Xét các biến cố sau:
E: “Bạn Hoàng lấy được quả cầu màu đen”.
F: “Bạn Hoàng lấy được quả cầu màu trắng và bạn Hải không rút được tấm thẻ A”.
Hãy mô tả các kết quả thuận lợi cho hai biến cố E và F.
Phương pháp giải:
a) Sử dụng kiến thức về phép thử để tìm phép thử: Một hoặc một số hành động, thực nghiệm được tiến hành liên tiếp hay đồng thời mà kết quả của chúng không thể biết được trước khi thực hiện nhưng có thể liệt kê các kết quả có thể xảy ra, được gọi là một phép thử ngẫu nhiên, gọi tắt là phép thử.
Có thể tìm không gian mẫu của phép tử bằng cách lập bảng.
b) Cách tìm kết quả thuận lợi của biến cố E.
+ Mô tả không gian mẫu của phép thử.
+ Tìm kết quả của phép thử làm cho biến cố xảy ra, đó là kết quả thuận lợi cho biến cố E.
Lời giải chi tiết:
a) Phép thử là Hoàng lấy ngẫu nhiên một quả cầu từ một túi đựng 2 quả cầu gồm một quả màu đen và một quả màu trắng, Hải rút ngẫu nhiên một tấm thẻ từ một hộp đựng 3 tấm thẻ A, B, C.
Kết quả của phép thử là (a, b) trong đó a và b tương ứng là màu của quả bóng và chữ ghi trên tấm thẻ.
Ta liệt kê được tất cả các kết quả có thể của phép thử bằng cách lập bảng:
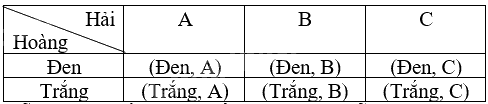
Mỗi ô là một kết quả có thể. Không gian mẫu là tập hợp 6 ô của bảng trên.
Do đó, không gian mẫu của phép thử là \(\Omega = \){(Đen, A), (Đen, B), (Đen, C), (Trắng, A), (Trắng, B), (Trắng, C)}.
b) Các kết quả thuận lợi của biến cố E là: (Đen, A), (Đen, B), (Đen, C).
Các kết quả thuận lợi của biến cố F là: (Trắng, B), (Trắng, C).
Mục 1 trang 60, 61 SGK Toán 9 tập 2 - Kết nối tri thức thường xoay quanh các chủ đề về hàm số bậc nhất, hệ số góc, và ứng dụng của hàm số trong việc giải quyết các bài toán thực tế. Việc nắm vững kiến thức về hàm số bậc nhất là nền tảng quan trọng cho các chương trình học toán ở các lớp trên.
Mục này thường bao gồm các bài tập sau:
Để xác định hệ số góc của đường thẳng có phương trình y = ax + b, ta chỉ cần xác định giá trị của a. Nếu đường thẳng đi qua hai điểm A(x1, y1) và B(x2, y2) thì hệ số góc được tính theo công thức:
a = (y2 - y1) / (x2 - x1)
Ví dụ: Cho đường thẳng đi qua A(1, 2) và B(3, 6). Hệ số góc của đường thẳng là:
a = (6 - 2) / (3 - 1) = 4 / 2 = 2
Nếu biết hệ số góc a và một điểm A(x0, y0) thuộc đường thẳng, phương trình đường thẳng có dạng:
y - y0 = a(x - x0)
Ví dụ: Viết phương trình đường thẳng có hệ số góc a = -1 và đi qua điểm A(2, 3). Phương trình đường thẳng là:
y - 3 = -1(x - 2) => y = -x + 5
Để tìm giao điểm của hai đường thẳng, ta giải hệ phương trình hai ẩn chứa phương trình của hai đường thẳng đó. Giao điểm là nghiệm của hệ phương trình.
Ví dụ: Tìm giao điểm của hai đường thẳng y = x + 1 và y = -x + 3.
Giải hệ phương trình:
{ y = x + 1y = -x + 3 }
=> x + 1 = -x + 3 => 2x = 2 => x = 1
=> y = 1 + 1 = 2
Vậy giao điểm của hai đường thẳng là (1, 2).
Hàm số bậc nhất có thể được sử dụng để mô tả mối quan hệ giữa hai đại lượng thay đổi. Ví dụ, ta có thể sử dụng hàm số bậc nhất để mô tả mối quan hệ giữa quãng đường đi được và thời gian đi với vận tốc không đổi.
Ví dụ: Một ô tô đi với vận tốc 60km/h. Hãy viết hàm số biểu thị quãng đường đi được (s) theo thời gian (t).
Hàm số có dạng: s = 60t
Việc giải mục 1 trang 60, 61 SGK Toán 9 tập 2 - Kết nối tri thức đòi hỏi sự hiểu biết về hàm số bậc nhất và các ứng dụng của nó. Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin hơn trong việc giải quyết các bài tập và đạt kết quả tốt trong môn Toán.