Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tại giaitoan.edu.vn. Bài viết này sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 87, 88 sách giáo khoa Toán 9 tập 1 chương trình Kết nối tri thức.
Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức. Vì vậy, đội ngũ giaitoan.edu.vn đã biên soạn bài giải này với mục tiêu giúp các em nắm vững kiến thức và tự tin giải quyết các bài tập tương tự.
Xét dây AB tùy ý không đi qua tâm của đường tròn (O; R) (H.5.7). Dựa vào quan hệ giữa các cạnh của tam giác AOB, chứng minh AB < 2R.
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 1 trang 88 SGK Toán 9 Kết nối tri thức
Cho đường tròn đường kính BC. Chứng minh rằng với điểm A bất kì (khác B và C) trên đường tròn, ta đều có: BC < AB + AC < 2BC
Phương pháp giải:
- Áp dụng bất đẳng thức trong tam giác ta có: BC < AB + AC.
- Theo quan hệ giữa dây và đường kính ta có: AB < BC, AC < BC
Do đó: AB + AC < 2BC.
Lời giải chi tiết:
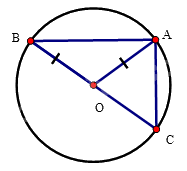
Xét tam giác ABC có: BC < AB + AC (bất đẳng thức tam giác) (1)
Xét đường tròn đường kính BC có dây cung AB, AC ta có: AB < BC, AC < BC
Suy ra: AB + AC < 2BC (2)
Từ (1) và (2) suy ra: BC < AB + AC < 2BC.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động trang 87 SGK Toán 9 Kết nối tri thức
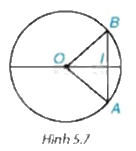
Xét dây AB tùy ý không đi qua tâm của đường tròn (O; R) (H.5.7). Dựa vào quan hệ giữa các cạnh của tam giác AOB, chứng minh AB < 2R.
Phương pháp giải:
Áp dụng bất đẳng thức tam giác đối với tam giác AOB.
Lời giải chi tiết:
Xét tam giác AOB có: AB < OA + OB (bất đẳng thức tam giác)
mà OA = OB = R nên AB < 2R.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động trang 87 SGK Toán 9 Kết nối tri thức
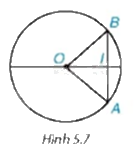
Xét dây AB tùy ý không đi qua tâm của đường tròn (O; R) (H.5.7). Dựa vào quan hệ giữa các cạnh của tam giác AOB, chứng minh AB < 2R.
Phương pháp giải:
Áp dụng bất đẳng thức tam giác đối với tam giác AOB.
Lời giải chi tiết:
Xét tam giác AOB có: AB < OA + OB (bất đẳng thức tam giác)
mà OA = OB = R nên AB < 2R.
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 1 trang 88 SGK Toán 9 Kết nối tri thức
Cho đường tròn đường kính BC. Chứng minh rằng với điểm A bất kì (khác B và C) trên đường tròn, ta đều có: BC < AB + AC < 2BC
Phương pháp giải:
- Áp dụng bất đẳng thức trong tam giác ta có: BC < AB + AC.
- Theo quan hệ giữa dây và đường kính ta có: AB < BC, AC < BC
Do đó: AB + AC < 2BC.
Lời giải chi tiết:
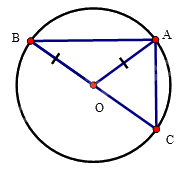
Xét tam giác ABC có: BC < AB + AC (bất đẳng thức tam giác) (1)
Xét đường tròn đường kính BC có dây cung AB, AC ta có: AB < BC, AC < BC
Suy ra: AB + AC < 2BC (2)
Từ (1) và (2) suy ra: BC < AB + AC < 2BC.
Mục 1 của chương trình Toán 9 tập 1 Kết nối tri thức tập trung vào việc ôn tập và hệ thống hóa kiến thức về hàm số bậc nhất. Các bài tập trong trang 87 và 88 SGK Toán 9 tập 1 yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Bài tập này yêu cầu học sinh xác định hệ số a của hàm số bậc nhất khi biết đồ thị của hàm số hoặc biết hai điểm thuộc đồ thị. Để giải bài tập này, học sinh cần nắm vững phương pháp tìm hệ số a thông qua việc sử dụng tọa độ của các điểm thuộc đồ thị.
Bài tập này yêu cầu học sinh vẽ đồ thị của hàm số bậc nhất khi biết hệ số a và b. Để vẽ đồ thị, học sinh cần xác định hai điểm thuộc đồ thị và nối chúng lại với nhau.
Bài tập này yêu cầu học sinh tìm giao điểm của hai đường thẳng. Để tìm giao điểm, học sinh cần giải hệ phương trình bậc nhất hai ẩn tương ứng với hai đường thẳng.
x + 1 = -x + 3
=> 2x = 2
=> x = 1
Thay x = 1 vào phương trình y = x + 1, ta được y = 2.
Vậy giao điểm của hai đường thẳng là (1; 2).
Ngoài các bài tập trong SGK, học sinh có thể tìm hiểu thêm về các ứng dụng của hàm số bậc nhất trong thực tế, như tính quãng đường đi được của một vật chuyển động đều, tính tiền lương theo sản lượng, tính giá trị của một hàng hóa khi có chiết khấu,...
Hy vọng bài giải chi tiết này sẽ giúp các em học sinh hiểu rõ hơn về các bài tập trong mục 1 trang 87, 88 SGK Toán 9 tập 1 - Kết nối tri thức. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!